A finitely presented 1-ended group $G$ has semistable fundamental group at infinity if $G$ acts geometrically on a simply connected and locally compact ANR $Y$ having the property that any two proper rays in $Y$ are properly homotopic. This property of $Y$ captures a notion of connectivity at infinity stronger than “1-ended”, and is in fact a feature of $G$, being independent of choices. It is a fundamental property in the homotopical study of finitely presented groups. While many important classes of groups have been shown to have semistable fundamental group at infinity, the question of whether every $G$ has this property has been a recognized open question for nearly forty years. In this paper we attack the problem by considering a proper but non-cocompact action of a group $J$ on such an $Y$. This $J$ would typically be a subgroup of infinite index in the geometrically acting over-group $G$; for example $J$ might be infinite cyclic or some other subgroup whose semistability properties are known. We divide the semistability property of $G$ into a $J$-part and a “perpendicular to $J$” part, and we analyze how these two parts fit together. Among other things, this analysis leads to a proof (in a companion paper) that a class of groups previously considered to be likely counter examples do in fact have the semistability property.

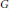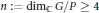Let $P$ be a maximal proper parabolic subgroup of a connected simple linear algebraic group $G$, defined over $\mathbb{C}$, such that $n\,:=\,{{\dim}_{\mathbb{C}}}\,G/P\,\ge \,4$. Let 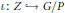$\iota :\,Z\,\to \,G/P$ be a reduced smooth hypersurface of degree at least 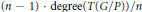$\left( n\,-\,1 \right)\,.\,\deg \text{ree}\left( T\left( G/P \right) \right)/n$. We prove that the restriction of the tangent bundle 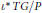${{\iota }^{*}}\,TG/P$ is semistable.

Let X be a geometrically irreducible smooth projective curve defined over a field k. Assume that X has a k–rational point; fix a k–rational point x ε X. From these data we construct an affine group scheme X defined over the field k as well as a principal X–bundle over the curve X. The group scheme X is given by a ℚ–graded neutral Tannakian category built out of all strongly semistable vector bundles over X. The principal bundle is tautological. Let G be a linear algebraic group, defined over k, that does not admit any nontrivial character which is trivial on the connected component, containing the identity element, of the reduced center of G. Let EG be a strongly semistable principal G–bundle over X. We associate to EG a group scheme M defined over k, which we call the monodromy group scheme of EG, and a principal M–bundle EM over X, which we call the monodromy bundle of EG. The group scheme M is canonically a quotient of X, and EM is the extension of structure group of . The group scheme M is also canonically embedded in the fiber Ad(EG)x over x of the adjoint bundle.