Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T20:48:03.858Z Has data issue: false hasContentIssue false
  • English
  • Français

Restriction of the Tangent Bundle of G/P to a Hypersurface

Published online by Cambridge University Press:  20 November 2018

Indranil Biswas
Indranil Biswas*
Affiliation:
School of Mathematics, Tata Institute of Fundamental Research, Homi Bhabha Road, Bombay 400005, India e-mail: indranil@math.tifr.res.in
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

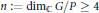Let $P$ be a maximal proper parabolic subgroup of a connected simple linear algebraic group $G$, defined over $\mathbb{C}$, such that $n\,:=\,{{\dim}_{\mathbb{C}}}\,G/P\,\ge \,4$. Let 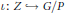$\iota :\,Z\,\to \,G/P$ be a reduced smooth hypersurface of degree at least 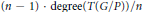$\left( n\,-\,1 \right)\,.\,\deg \text{ree}\left( T\left( G/P \right) \right)/n$. We prove that the restriction of the tangent bundle 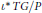${{\iota }^{*}}\,TG/P$ is semistable.

Keywords

14F0514J6014M15tangent bundlehomogeneous spacesemistabilityhypersurface
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 53 , Issue 2 , 01 June 2010 , pp. 218 - 222
Copyright
Copyright © Canadian Mathematical Society 2010

References

[Br] Broer, A., A vanishing theorem for Dolbeault cohomology of homogeneous vector bundles. J. Reine Angew. Math. 493(1997), 153–169.Google Scholar
[Fl] Flenner, H., Restrictions of semistable bundles on projective varieties. Comment. Math. Helv. 59(1984), no. r4, 635–650. doi:10.1007/BF02566370Google Scholar
[Gr] Grothendieck, A., Cohomologie locale des faisceaux cohérents et théorĕmes de Lefschetz locaux et globaux. (SGA 2). Advanced Studies in Pure Mathematics, Vol. 2. North-Holland Publishing, Paris, 1968.Google Scholar
[Ko] Kobayashi, S., Differential Geometry of Complex Vector Bundles. Publications of the Mathematical Society of Japan 15. Princeton University Press, Princeton, NJ, 1987.Google Scholar
[Pa] Paoletti, R., Stability of Kapranov bundles on quadrics. Ann. Mat. Pura. Appl. 169(1995), 109–124. doi:10.1007/BF01759351Google Scholar
[RR] Ramanan, S. and Ramanathan, A., Some remarks on the instability flag. Tôhoku Math. J. 36(1984), no. 2, 269–291. doi:10.2748/tmj/1178228852Google Scholar
[Um] Umemura, H., On a theorem of Ramanan. Nagoya Math. Jour. 69(1978), 131–138.Google Scholar