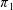A well-known conjecture is that all finitely presented groups have semistable fundamental groups at infinity. A class of groups whose members have not been shown to be semistable at infinity is the class 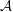 ${\mathcal{A}}$ of finitely presented groups that are ascending HNN-extensions with finitely generated base. The class
${\mathcal{A}}$ of finitely presented groups that are ascending HNN-extensions with finitely generated base. The class 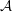 ${\mathcal{A}}$ naturally partitions into two non-empty subclasses, those that have “bounded” and “unbounded” depth. Using new methods introduced in a companion paper we show those of bounded depth have semistable fundamental group at infinity. Ascending HNN extensions produced by Ol’shanskii–Sapir and Grigorchuk (for other reasons), and once considered potential non-semistable examples are shown to have bounded depth. Finally, we devise a technique for producing explicit examples with unbounded depth. These examples are perhaps the best candidates to date in the search for a group with non-semistable fundamental group at infinity.
${\mathcal{A}}$ naturally partitions into two non-empty subclasses, those that have “bounded” and “unbounded” depth. Using new methods introduced in a companion paper we show those of bounded depth have semistable fundamental group at infinity. Ascending HNN extensions produced by Ol’shanskii–Sapir and Grigorchuk (for other reasons), and once considered potential non-semistable examples are shown to have bounded depth. Finally, we devise a technique for producing explicit examples with unbounded depth. These examples are perhaps the best candidates to date in the search for a group with non-semistable fundamental group at infinity.
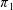 $\unicode[STIX]{x1D70B}_{1}$-Semistability at infinity
$\unicode[STIX]{x1D70B}_{1}$-Semistability at infinity