Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-13T06:25:47.451Z Has data issue: false hasContentIssue false
  • English
  • Français

Bounded Depth Ascending HNN Extensions and 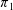$\unicode[STIX]{x1D70B}_{1}$-Semistability at infinity

Part of: Structure and classification of infinite or finite groups Special aspects of infinite or finite groups

Published online by Cambridge University Press:  22 July 2019

Michael L. Mihalik
Michael L. Mihalik*
Affiliation:
Department of Mathematics, Vanderbilt University, Nashville, TN, USA Email: michael.l.mihalik@vanderbilt.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

A well-known conjecture is that all finitely presented groups have semistable fundamental groups at infinity. A class of groups whose members have not been shown to be semistable at infinity is the class 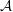${\mathcal{A}}$ of finitely presented groups that are ascending HNN-extensions with finitely generated base. The class 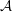${\mathcal{A}}$ naturally partitions into two non-empty subclasses, those that have “bounded” and “unbounded” depth. Using new methods introduced in a companion paper we show those of bounded depth have semistable fundamental group at infinity. Ascending HNN extensions produced by Ol’shanskii–Sapir and Grigorchuk (for other reasons), and once considered potential non-semistable examples are shown to have bounded depth. Finally, we devise a technique for producing explicit examples with unbounded depth. These examples are perhaps the best candidates to date in the search for a group with non-semistable fundamental group at infinity.

Keywords

ascending HNN extensionfundamental group at infinitysemistability at infinity

MSC classification

Primary: 20F69: Asymptotic properties of groups
Secondary: 20F65: Geometric group theory 20E22: Extensions, wreath products, and other compositions
Type
Article
Information
Canadian Journal of Mathematics , Volume 72 , Issue 6 , December 2020 , pp. 1529 - 1550
Check for updates
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Conner, G. R. and Mihalik, M. L., Commensurated subgroups, semistability and simple connectivity at infinity. Algebr. Geom. Topol. 14(2014), no. 6, 3509–3532. https://doi.org/10.2140/agt.2014.14.3509CrossRefGoogle Scholar
Geoghegan, R. and Guilbault, C. R., Topological properties of spaces admitting free group actions. J. Topol. 5(2012), no. 2, 249–275. https://doi.org/10.1112/jtopol/jts002CrossRefGoogle Scholar
Geoghegan, R., Guilbault, C., and Mihalik, M., Non-cocompact group actions and $\unicode[STIX]{x1D70B}_{1}$-semistability at infinity. Preprint, 2016.Google Scholar
Geoghegan, R., Guilbault, C., and Mihalik, M., Topological properties of spaces admitting a coaxial homeomorphism. Preprint, 2016.Google Scholar
Grigorchuk, R. I., On a problem of M. Day on nonelementary amenable groups in the class of finitely presented groups. Mat. Zametki 60(1996), no. 5, 774–775. https://doi.org/10.1007/BF02309174Google Scholar
Grigorchuk, R. I., An example of a finitely presented amenable group that does not belong to the class EG. Mat. Sb. 189(1998), no. 1, 79–100. https://doi.org/10.1070/SM1998v189n01ABEH000293Google Scholar
Lysënok, I. G., A set of defining relations for the Grigorchuk group. Mat. Zametki 38(1985), no. 4, 503–516, 634.Google Scholar
Mihalik, M. L., Semistability and simple connectivity at ∞ of finitely generated groups with a finite series of commensurated subgroups. Algebr. Geom. Topol. 16(2016), no. 6, 3615–3640. https://doi.org/10.2140/agt.2016.16.3615CrossRefGoogle Scholar
Mihalik, M. L., Semistability at the end of a group extension. Trans. Amer. Math. Soc. 277(1983), no. 1, 307–321. https://doi.org/10.2307/1999358CrossRefGoogle Scholar
Mihalik, M. L., Ends of groups with the integers as quotient. J. Pure Appl. Algebra 35(1985), no. 3, 305–320.CrossRefGoogle Scholar
Mihalik, M. L., Semistability at ∞ of finitely generated groups, and solvable groups. Topology Appl. 24(1986), no. 1-3, 259–269. https://doi.org/10.1016/0166-8641(86)90069-6CrossRefGoogle Scholar
Ol’shanskii, A. Yu. and Sapir, M. V., Non-amenable finitely presented torsion-by-cyclic groups. Electron. Res. Announc. Amer. Math. Soc. 7(2001), 63–71. https://doi.org/10.1090/S1079-6762-01-00095-6CrossRefGoogle Scholar
Ol’shanskii, A. Y. and Sapir, M. V., Non-amenable finitely presented torsion-by-cyclic groups. Publ. Math. Inst. Hautes Études Sci.(2002), no. 96, 43–169. (2003).Google Scholar
Wright, D. G., Contractible open manifolds which are not covering spaces. Topology 31(1992), no. 2, 281–291. https://doi.org/10.1016/0040-9383(92)90021-9CrossRefGoogle Scholar