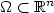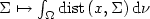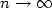The purpose of this paper is to provide further understanding into the structure of the sequential allocation (“stochastic multi-armed bandit”) problem by establishing probability one finite horizon bounds and convergence rates for the sample regret associated with two simple classes of allocation policies. For any slowly increasing function g, subject to mild regularity constraints, we construct two policies (the g-Forcing, and the g-Inflated Sample Mean) that achieve a measure of regret of order O(g(n)) almost surely as n → ∞, bound from above and below. Additionally, almost sure upper and lower bounds on the remainder term are established. In the constructions herein, the function g effectively controls the “exploration” of the classical “exploration/exploitation” tradeoff.