Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T19:59:33.729Z Has data issue: false hasContentIssue false
  • English
  • Français

Long-term planning versus short-term planning in the asymptotical location problem

Published online by Cambridge University Press:  30 May 2008

Alessio Brancolini ,
Giuseppe Buttazzo ,
Filippo Santambrogio  and
Eugene Stepanov
Alessio Brancolini
Affiliation:
SISSA, 4 via Beirut, 34014 Trieste, Italy; brancoli@sissa.it
Giuseppe Buttazzo
Affiliation:
Dipartimento di Matematica, Università di Pisa, 5 Largo B. Pontecorvo, 56127 Pisa, Italy; buttazzo@dm.unipi.it
Filippo Santambrogio
Affiliation:
CEREMADE, Université Paris-Dauphine, Place du Maréchal de Lattre de Tassigny, 75775 Paris Cedex 16, France; santambrogio@ceremade.dauphine.fr
Eugene Stepanov
Affiliation:
Dipartimento di Matematica, Università di Pisa, 5 Largo B. Pontecorvo, 56127 Pisa, Italy; stepanov.eugene@gmail.com
Get access

Abstract

Given the probability measure ν over the given region $\Omega\subset \mathbb{R}^n$ 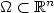, we consider the optimal location of a setΣ composed by n points in Ω in order to minimize theaverage distance $\Sigma\mapsto \int_\Omega \mathrm{dist}\,(x,\Sigma)\,{\rm d}\nu$ 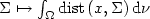(theclassical optimal facility location problem). The paper compares twostrategies to find optimal configurations: the long-term one whichconsists in placing all n points at once in an optimal position, and the short-term one which consists in placing the points one by one addingat each step at most one point and preserving the configurationbuilt at previous steps. We show that the respective optimizationproblems exhibit qualitatively different asymptotic behavior as $n\to\infty$ 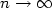, although the optimization costs in both cases have the same asymptotic orders of vanishing.

Keywords

Location problemfacility locationFermat-Weber problemk-median problemsequential allocationaverage distance functionaloptimal transportation
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 15 , Issue 3 , July 2009 , pp. 509 - 524
Copyright
© EDP Sciences, SMAI, 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ambrosio, L., Minimizing movements. Rend. Accad. Naz. Sci. XL Mem. Mat. Appl. 19 (1995) 191–246.
L. Ambrosio, N. Gigli and G. Savarè, Gradient flows in metric spaces and in the spaces of probability measures, Lectures in Mathematics. ETH Zurich, Birkhäuser (2005).
Bouchitté, G., Jimenez, C. and Rajesh, M., Asymptotique d'un problème de positionnement optimal. C. R. Acad. Sci. Paris Ser. I 335 (2002) 1–6. CrossRef
Brancolini, A. and Buttazzo, G., Optimal networks for mass transportation problems. ESAIM: COCV 11 (2005) 88–101. CrossRef
G. Buttazzo and E. Stepanov, Optimal transportation networks as free Dirichlet regions for the Monge-Kantorovich problem. Ann. Scuola Norm. Sup. Cl. Sci. II (2003) 631–678.
G. Buttazzo and E. Stepanov, Minimization problems for average distance functionals, in Calculus of Variations: Topics from the Mathematical Heritage of Ennio De Giorgi, D. Pallara Ed., Quaderni di Matematica 14, Seconda Universita di Napoli (2004) 47–83.
G. Buttazzo, E. Oudet and E. Stepanov, Optimal transportation problems with free Dirichlet regions, Progress in Nonlinear Differential Equations and their Applications 51. Birkhäuser (2002) 41–65.
G. Dal Maso, An introduction to Γ-convergence. Birkhauser, Basel (1992).
L. Fejes Töth, Lagerungen in der Ebene auf der Kugel und im Raum, Die Grundlehren der Math. Wiss. 65. Springer-Verlag, Berlin (1953).
Morgan, F. and Bolton, R., Hexagonal economic regions solve the location problem. Amer. Math. Monthly 109 (2002) 165–172. CrossRef
Mosconi, S.J.N. and Tilli, P., Γ-convergence for the irrigation problem. J. Convex Anal. 12 (2005) 145–158.
Paolini, E. and Stepanov, E., Qualitative properties of maximum distance minimizers and average distance minimizers in $\mathbb{R}^n$ . J. Math. Sciences (N.Y.) 122 (2004) 105–122.
Santambrogio, F. and Tilli, P., Blow-up of optimal sets in the irrigation probem. J. Geom. Anal. 15 (2005) 343–362. CrossRef
Stepanov, E., Partial geometric regularity of some optimal connected transportation networks. J. Math. Sciences (N.Y.) 132 (2006) 522–552. CrossRef
Suzuki, A. and Drezner, Z., The p-center location. Location Sci. 4 (1996) 69–82. CrossRef
A. Suzuki and A. Okabe, Using Voronoi diagrams, in Facility location: a survey of applications and methods, Z. Drezner Ed., Springer Series in Operations Research, Springer Verlag (1995) 103–118.
Suzuki, T., Asami, Y. and Okabe, A., Sequential location-allocation of public facilities in one- and two-dimensional space: comparison of several policies. Math. Program. Ser. B 52 (1991) 125–146. CrossRef
http://cvgmt.sns.it/papers/brabutsan06/.