In this paper we introduce a set of orthonormal functions, 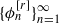 , where ϕn[r] is composed of a sine function and a sigmoidal transformation γr of order r>0. Based on the proposed functions ϕn[r] named by sigmoidal sine functions, we consider a series expansion of a function on the interval [−1,1] and the related convergence analysis. Furthermore, we extend the sigmoidal transformation to the whole real line ℝ and then, by reconstructing the existing sigmoidal cosine functions ψn[r] and the presented functions ϕn[r], we develop two kinds of 2-periodic series expansions on ℝ. Superiority of the presented sigmoidal-type series in approximating a function by the partial sum is demonstrated by numerical examples.
, where ϕn[r] is composed of a sine function and a sigmoidal transformation γr of order r>0. Based on the proposed functions ϕn[r] named by sigmoidal sine functions, we consider a series expansion of a function on the interval [−1,1] and the related convergence analysis. Furthermore, we extend the sigmoidal transformation to the whole real line ℝ and then, by reconstructing the existing sigmoidal cosine functions ψn[r] and the presented functions ϕn[r], we develop two kinds of 2-periodic series expansions on ℝ. Superiority of the presented sigmoidal-type series in approximating a function by the partial sum is demonstrated by numerical examples.

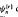 composed of a cosine function and a sigmoidal transformation γ
composed of a cosine function and a sigmoidal transformation γ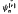 converges uniformly to
converges uniformly to 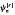 according to the value of
according to the value of 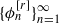 , where ϕ
, where ϕ