Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-27T13:17:17.792Z Has data issue: false hasContentIssue false
  • English
  • Français

Sigmoidal cosine series on the interval

Published online by Cambridge University Press:  17 February 2009

Beong In Yun
Beong In Yun
Affiliation:
Faculty of Mathematics, Informatics and Statistics, Kunsan National University, 573–701, Korea; e-mail: biyun@kunsan.ac.kr or paulll@maths.uq.edu.au.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We construct a set of functions, say, 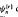composed of a cosine function and a sigmoidal transformation γr of order r > 0. The present functions are orthonormal with respect to a proper weight function on the interval [−1, 1]. It is proven that if a function f is continuous and piecewise smooth on [−1, 1] then its series expansion based on 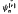converges uniformly to f so long as the order of the sigmoidal transformation employed is 0 < r ≤ 1. Owing to the variational feature of 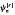according to the value of r, one can expect improvement of the traditional Fourier series approximation for a function on a finite interval. Several numerical examples show the efficiency of the present series expansion in comparison with the Fourier series expansion.

Keywords

Fourier seriessigmoidal transformationsigmoidal cosine series.
Type
Research Article
Information
The ANZIAM Journal , Volume 47 , Issue 4 , April 2006 , pp. 451 - 475
Copyright
Copyright © Australian Mathematical Society 2006

References

[1]Choi, U. J., Kim, S. W. and Yun, B. I., “Improvement of the asymptotic behavior of the EulerMaclaurin formula for Cauchy principal value and Hadamard finite-part integrals”, Int. J. Numer Meth. Engng. 61 (2004) 496–513.CrossRefGoogle Scholar
[2]Elliott, D., “The Euler-Maclaurin formula revisited”, J. Austral. Math. Soc. Ser. B 40(E) (1998) E27–E76.Google Scholar
[3]Elliott, D., “Sigmoidal transformations and the trapezoidal rule”, J. Austral. Math. Soc. Ser. B 40(E) (1998) E77–E137.Google Scholar
[4]Elliott, D. and Venturino, E., “Sigmoidal transformations and the Euler-Maclaurin expansion for evaluating certain Hadamard finite-part integrals”, Numer Math. 77 (1997) 453–465.CrossRefGoogle Scholar
[5]Folland, G. B., Fourier Analysis and Its Applications(Wadsworth & Brooks/Cole, 1992).Google Scholar
[6]Gradshteyn, I. S. and Ryzhik, I. M., Table of Integrals, Series, and Products, 6th ed. (Academic Press, San Diego, CA, 2000).Google Scholar
[7]Jerri, A. J., The Gibbs Phenomenon in Fourier Analysis, Splines and Wavelet Approximations (Kluwer Academic Publisher, Dordrecht, 1998).CrossRefGoogle Scholar
[8]Johnston, P. R., “Application of sigmoidal transformations to weakly singular and near singular boundary element integrals”, Int. J. Numer. Meth. Engng. 45 (1999) 1333–1348.3.0.CO;2-Q>CrossRefGoogle Scholar
[9]Pinkus, A. and Zafrany, S., Fourier Analysis and Integral Transforms (Cambridge University Press, Cambridge, 1997).Google Scholar
[10]Prössdorf, S. and Rathsfeld, A., “On an integral equation of the first kind arising from a cruciform crack problem”, in Integral Equations and Inverse Problems (eds. Petkov, V. and Lazarov, R.), (Longman, Harlow, 1991) 210–219.Google Scholar
[11]Sidi, A., “A new variable transformation for numerical integration”, in Numerical Integration IV ISNM Vol. 112 (eds. Brass, H. and Hämmerlin, G.), (Birkhaüser, Basel, 1993) 359–373.Google Scholar
[12]Yun, B. I., “An extended sigmoidal transformation technique for evaluating weakly singular integrals without splitting the integration interval”, SIAM J. Sci. Comput. 25 (2003) 284–301.CrossRefGoogle Scholar
[13]Yun, B. I., “A generalized non-linear transformation for evaluating singular integrals”, Int. J. Numer. Meth. Engng. 65 (2006) 1947–1969.CrossRefGoogle Scholar
[14]Yun, B. I. and Kim, P., “A new sigmoidal transformation for weakly singular integrals in the boundary element method”, SIAM J. Sci. Comput. 24 (2003) 1203–1217.CrossRefGoogle Scholar