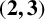 $\boldsymbol {(2,3)}$-GENERATION OF THE FINITE SIMPLE ODD-DIMENSIONAL ORTHOGONAL GROUPS
$\boldsymbol {(2,3)}$-GENERATION OF THE FINITE SIMPLE ODD-DIMENSIONAL ORTHOGONAL GROUPS
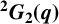 $\boldsymbol {{}^{2}G_{2}(q)}$ USING THE CODEGREE SET
$\boldsymbol {{}^{2}G_{2}(q)}$ USING THE CODEGREE SET

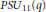 $PS{{U}_{11}}(q)$
$PS{{U}_{11}}(q)$