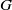Refine search
Actions for selected content:
2 results
A NOTE ON THE WEISS CONJECTURE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 07 August 2013, pp. 356-361
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
Hyperbolic Polynomials and Convex Analysis
-
- Journal:
- Canadian Journal of Mathematics / Volume 53 / Issue 3 / 01 June 2001
- Published online by Cambridge University Press:
- 20 November 2018, pp. 470-488
- Print publication:
- 01 June 2001
-
- Article
-
- You have access
- Export citation