Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-10T16:28:46.084Z Has data issue: false hasContentIssue false
  • English
  • Français

Hyperbolic Polynomials and Convex Analysis

Published online by Cambridge University Press:  20 November 2018

Heinz H. Bauschke ,
Osman Güler ,
Adrian S. Lewis  and
Hristo S. Sendov
Heinz H. Bauschke
Affiliation:
Department of Mathematics and Statistics Okanagan University College Kelowna, British Columbia V1V 1V7, email: bauschke@cecm.sfu.ca
Osman Güler
Affiliation:
Department of Mathematics and Statistics University of Maryland Baltimore County Baltimore, Maryland 21228, USA, email: guler@math.umbc.edu
Adrian S. Lewis
Affiliation:
Department of Combinatorics & Optimization University of Waterloo Waterloo, Ontario N2L 3G1, email: aslewis@math.uwaterloo.ca
Hristo S. Sendov
Affiliation:
Department of Combinatorics & Optimization University of Waterloo Waterloo, Ontario N2L 3G1, email: hssendov@barrow.uwaterloo.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

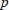A homogeneous real polynomial $p$ is hyperbolic with respect to a given vector $d$ if the univariate polynomial 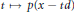$t\,\mapsto \,p(x\,-\,td)$ has all real roots for all vectors 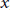$x$. Motivated by partial differential equations, Gårding proved in 1951 that the largest such root is a convex function of 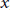$x$, and showed various ways of constructing new hyperbolic polynomials. We present a powerful new such construction, and use it to generalize Gårding’s result to arbitrary symmetric functions of the roots. Many classical and recent inequalities follow easily. We develop various convex-analytic tools for such symmetric functions, of interest in interior-point methods for optimization problems over related cones.

Keywords

90C2515A4552A41convex analysiseigenvalueGårding’s inequalityhyperbolic barrier functionhyperbolic polynomialhyperbolicity coneinterior-point methodsemidefinite programsingular valuesymmetric functionunitarily invariant norm
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 53 , Issue 3 , 01 June 2001 , pp. 470 - 488
Copyright
Copyright © Canadian Mathematical Society 2001

References

[1] Bauschke, H. H., Lewis, A. S., Güler, O., and Sendov, H. S., Hyperbolic Polynomials and Convex Analysis. Research Report CORR 98-29, Department of Combinatorics and Optimization, University of Waterloo, June 1998.Google Scholar
[2] Beckenbach, E. F. and Bellman, R., Inequalities. Springer-Verlag, 1961.Google Scholar
[3] Bhatia, R., Matrix Analysis. Springer-Verlag, 1997.Google Scholar
[4] Bullen, P. and Marcus, M., Symmetric means and matrix inequalities. Proc. Amer.Math. Soc. 12 (1961), 285–290.Google Scholar
[5] Bullen, P. S., Mitrinović, D. S. and Vasić, P. M., Means and Their Inequalities. Math. Appl. (East European Ser.), D. Reidel Publishing Company, Dordrecht, Holland, 1987.Google Scholar
[6] Davis, C., All convex invariant functions of hermitian matrices. Arch. Math. 8 (1957), 276–278.Google Scholar
[7] Fan, Ky, On a theorem of Weyl concerning eigenvalues of linear transformations II. Proc. Nat. Acad. Sci. U.S.A. 36 (1950), 31–35.Google Scholar
[8] Gårding, L., Linear hyperbolic differential equations with constant coefficients. Acta Math. 85 (1951), 2–62.Google Scholar
[9] Gårding, L., An inequality for hyperpolic polynomials. J. Math. Mech. (6) 8 (1959), 957–965.Google Scholar
[10] Greub, W. H., Multilinear Algebra. Springer-Verlag, 1967.Google Scholar
[11] Güler, O., Hyperbolic polynomials and interior point methods for convex programming. Math. Oper. Res. (2) 22 (1997), 350–377.Google Scholar
[12] Hardy, G. H., Littlewood, J. E. and Pólya, G., Inequalities. Cambridge University Press, 2nd edition, 1952.Google Scholar
[13] Hiriart-Urruty, J.-B. and Ye, D., Sensitivity analysis of all eigenvalues of a symmetric matrix. Numer. Math. 70 (1992), 45–72.Google Scholar
[14] Hörmander, L., Notions of Convexity. Progress in Mathematics 127, Birkhäuser, Boston, 1994.Google Scholar
[15] Horn, R. A. and Johnson, C. R., Matrix Analysis. Cambridge University Press, 2nd edition, 1985.Google Scholar
[16] Horn, R. A. and Johnson, C. R., Topics in Matrix Analysis. Cambridge University Press, 1st edition, 1991; paperback edition with corrections, 1994.Google Scholar
[17] Hungerford, T. W., Algebra. Graduate Texts in Math. 73, Springer-Verlag, New York, 1974.Google Scholar
[18] Khovanskii, A. G., Analogues of the Aleksandrov-Fenchel inequalities for hyperbolic forms. Soviet Math. Dokl. 29 (1984), 710–713.Google Scholar
[19] Krylov, N. V., On the general notion of fully nonlinear second-order elliptic equations. Trans. Amer. Math. Soc. (3) 347 (1995), 857–895.Google Scholar
[20] Lax, P. D., Differential equations, difference equations and matrix theory. Comm. Pure Applied Math. 11 (1958), 175–194.Google Scholar
[21] Lewis, A. S., Convex analysis on the Hermitian matrices. SIAM J. Optim. (1) 6 (1996), 164–177.Google Scholar
[22] Lewis, A. S., Group invariance and convex matrix analysis. SIAMJ.Matrix Anal. Appl. (4) 17 (1996), 927–949.Google Scholar
[23] Lewis, A. S., Lidskii's theorem via nonsmooth analysis. SIAM J. Matrix Anal. Appl. 21 (1999), 379–381.Google Scholar
[24] Lewis, A. S. and Overton, M. L., Eigenvalue optimization. Acta Numerica 5 (1996), 149–190.Google Scholar
[25] Marcus, M. and Lopes, L., Inequalities for symmetric functions and Hermitian matrices. Canad. J. Math. 9 (1957), 305–312.Google Scholar
[26] Marcus, M. and Minc, H., The invariance of symmetric functions of singular values. Pacific J. Math. 12 (1962), 327–332.Google Scholar
[27] Marshall, A. W. and Olkin, I., Inequalities: Theory of Majorization and Its Applications. Mathematics in Science and Engineering 143, Academic Press, New York, 1979.Google Scholar
[28] McLeod, J. B., On four inequalities in symmetric functions. Proc. Edinburgh Math. Soc. 11(1958/1959), 211–219.Google Scholar
[29] Mitrinović, D. S., Analytic Inequalities. Die Grundlehren der mathematischenWisenschaften, Band 1965; Springer-Verlag, New York, 1970.Google Scholar
[30] Mitrinović, D. S., Pečarić, J. E. and Fink, A. M., Classical and New Inequalities in Analysis. Math. Appl. (East European Ser.) 61, Kluwer, 1993.Google Scholar
[31] Ostrowski, A. M., Solution of Equations in Euclidean and Banach Spaces. Academic Press, New York, 3rd edition, 1973.Google Scholar
[32] Rockafellar, R. T., Convex Analysis. Princeton University Press, Princeton, NJ, 1970.Google Scholar
[33] von Neumann, J., Some matrix inequalities and metrization of matric-space. Tomsk University Review 1 (1937), 286–300. In: Collected Works vol. IV, Pergamon, Oxford, 1962, 205–218.Google Scholar