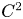In the context of discrete nonautonomous dynamics, we prove that the homeomorphisms in the linearization theorem are $C^2$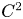 diffeomorphisms. In contrast to other related works, our result does not involve non-resonance conditions or spectral gaps. Our approach is based on the interlacing of the properties of nonautonomous hyperbolicity of the linear part, and boundedness and Lipschitzness of the nonlinearities. Moreover, we propose a functional approach to find conditions for regularity of arbitrary degree.
diffeomorphisms. In contrast to other related works, our result does not involve non-resonance conditions or spectral gaps. Our approach is based on the interlacing of the properties of nonautonomous hyperbolicity of the linear part, and boundedness and Lipschitzness of the nonlinearities. Moreover, we propose a functional approach to find conditions for regularity of arbitrary degree.