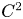1. Introduction
The well-known Hartman–Grobman theorem [Reference Hartman13, theorem I] is an essential tool in the study of local behaviour of autonomous and nonautonomous nonlinear dynamical systems. This theorem establishes a local topological conjugacy between the continuous dynamical system given by a $C^1$![]() diffeomorphism of the space $\mathbb {R}^d$
diffeomorphism of the space $\mathbb {R}^d$![]() and its linearization around an hyperbolic equilibrium, i.e. the dynamics near the equilibrium points are topologically the same. This result helps to design local phase portraits around all equilibria.
and its linearization around an hyperbolic equilibrium, i.e. the dynamics near the equilibrium points are topologically the same. This result helps to design local phase portraits around all equilibria.
The global behaviour study begins when Pugh [Reference Pugh17] studied a particular case of the Hartman–Grobman's theorem focused on linear systems with bounded and Lipschitz perturbations allowing the construction of an explicit and global homeomorphism, but without considering its smoothness properties. This work inspired Palmer [Reference Palmer15] to achieve the first result of global linearization in the nonautonomous framework: the Hartman–Grobman theorem for nonautonomous differential equations. This seminal article considered vector fields whose linear component inherits, in some sense, the hyperbolicity property of the autonomous case, namely uniform exponential dichotomy property (see [Reference Coffman and Schäffer8, Reference Coppel9] for more information about this property); while the nonlinear parts of the vector fields are bounded and Lipschitzian.
Although the task of finding such a homeomorphism is delicate, to show that it has a class of differentiability is an inherently more interesting challenge in dynamics, since this allows a better understanding of the information that is carried from one system to another. In this sense, in the autonomous framework, Sternberg [Reference Sternberg20, Reference Sternberg21] proved that under certain non-resonance conditions the local conjugation between two systems can actually be a $C^r$![]() ($r\geq 0$
($r\geq 0$![]() ) map. Later, Belickiĭ [Reference Belickiĭ3, Reference Belickiĭ4] achieved the same result under assumptions related to the spectrum of the diffeomorphism that defines the dynamics.
) map. Later, Belickiĭ [Reference Belickiĭ3, Reference Belickiĭ4] achieved the same result under assumptions related to the spectrum of the diffeomorphism that defines the dynamics.
Nevertheless, to the best of our knowledge, there are no results about the differentiability of Palmer's linearization prior to this study [Reference Castañeda and Robledo7], which establishes that, under some technical assumptions, a orientation preserving linearization of class $C^2$![]() exists. For a recent generalization and improvement of this result, we refer the reader to [Reference Castañeda, Monzón and Robledo6].
exists. For a recent generalization and improvement of this result, we refer the reader to [Reference Castañeda, Monzón and Robledo6].
Noteworthy is that there is also a recent study by Cuong et al. [Reference Cuong, Doan and Siegmund10], which extends the Sternberg theorem [Reference Sternberg20, Reference Sternberg21] to the nonautonomous case, i.e. a non-resonance condition related to Sacker–Sell spectrum is satisfied in order to obtain smooth local linearization; for more details on spectrum mentioned above, we refer the reader to [Reference Sacker and Sell18] and [Reference Kloeden and Rasmussen14, chapter 5]. Additionally, there is an interesting and novel approach given by Dragičević et al. in [Reference Dragičević, Zhang and Zhang12], where a nonuniform spectral bound condition is given for ensuring that the linearization of the perturbed system to be simultaneously differentiable at $0$![]() and Hölder continuous linearization in a neighbourhood of $0;$
and Hölder continuous linearization in a neighbourhood of $0;$![]() we point out that in this work the authors assume that the linear system has a nonuniform strong exponential dichotomy and the spectrum of the linear part is addressed in terms of a time-discrete evolution operator.
we point out that in this work the authors assume that the linear system has a nonuniform strong exponential dichotomy and the spectrum of the linear part is addressed in terms of a time-discrete evolution operator.
In [Reference Dragičević, Zhang and Zhang11] Dragičević et al., in a discrete nonautonomous framework, investigate $C^1$![]() smooth linearization with a nonuniform strong exponential dichotomy in the linear part. The main idea of the authors was to convert the linear part of the nonautonomous system to an autonomous one in order to obtain a spectral gap condition for $C^1$
smooth linearization with a nonuniform strong exponential dichotomy in the linear part. The main idea of the authors was to convert the linear part of the nonautonomous system to an autonomous one in order to obtain a spectral gap condition for $C^1$![]() linearization of first-order nonautonomous difference equation. On the contrary, in [Reference Barreira and Valls2], Barreira and Valls discussed Hölder continuous linearization with nonuniform dichotomy, however the smoothness is not considered.
linearization of first-order nonautonomous difference equation. On the contrary, in [Reference Barreira and Valls2], Barreira and Valls discussed Hölder continuous linearization with nonuniform dichotomy, however the smoothness is not considered.
Our work follows the results initiated in [Reference Castañeda and Robledo7], and is strongly based on the study of discrete framework expressed in [Reference Castañeda, González and Robledo5], since we use some of their results and strategies to find a Palmer's homeomorphism. The main difference between our work and [Reference Castañeda, González and Robledo5], in terms of differentiability, is that we allow the existence of nonempty unstable manifolds for the linear system; furthermore, our analysis neither involves a change from a nonautonomous environment to an autonomous one nor the use of spectral gaps in order to obtain $C^1$![]() -differentiability such as employed in [Reference Dragičević, Zhang and Zhang11]. Also our results do not include the autonomous case. Another interesting fact of our work is that differentiability is reached when in the linear part a wider family of dichotomies is considered.
-differentiability such as employed in [Reference Dragičević, Zhang and Zhang11]. Also our results do not include the autonomous case. Another interesting fact of our work is that differentiability is reached when in the linear part a wider family of dichotomies is considered.
Our paper is organized as follows. In § 2 we establish the nonautonomous tools in order to achieve the main results in this work. In § 3 we state a couple of results, that show some class of differentiability of the homeomorphisms, by using interlacing properties of hyperbolicity of the linear system, and boundedness and Lipschitzness of the nonlinear part. Moreover, we give examples of systems in order to achieve the conditions that allow homeomorphisms to have these classes of regularity. In § 4 we study a generalization of the previous conditions in order to obtain $C^2$![]() differentiability. Finally, in the last section, we propose an algebraic set of functions and an operator that can be inductively applied in order to find conditions for arbitrary high-order derivatives.
differentiability. Finally, in the last section, we propose an algebraic set of functions and an operator that can be inductively applied in order to find conditions for arbitrary high-order derivatives.
2. Preliminaries
Inspired by Palmer's work [Reference Palmer15], we studied the following nonautonomous discrete systems:
and
where $A:\mathbb {Z}^+\to \mathcal {M}_{d\times d}(\mathbb {R})$![]() is nonsingular (i.e. has invertible images) and uniformly bounded, i.e.
is nonsingular (i.e. has invertible images) and uniformly bounded, i.e.

We denote $j\mapsto x(j,m,\xi )$![]() and $j\mapsto y(j,m,\eta )$
and $j\mapsto y(j,m,\eta )$![]() the solutions of (2.1) and (2.2) which, respectively, take the value $\xi$
the solutions of (2.1) and (2.2) which, respectively, take the value $\xi$![]() and $\eta$
and $\eta$![]() when $j=m$
when $j=m$![]() .
.
The function $f:\mathbb {Z}^+\times \mathbb {R}^d\to \mathbb {R}^d$![]() is such that there exist sequences $\mu, \gamma :\mathbb {Z}^+\to \mathbb {R}^+$
is such that there exist sequences $\mu, \gamma :\mathbb {Z}^+\to \mathbb {R}^+$![]() verifying, for every $k\in \mathbb {Z}^+$
verifying, for every $k\in \mathbb {Z}^+$![]() and every pair
and every pair ![]() $(y,\tilde {y})\in \mathbb {R}^d\times \mathbb {R}^d$, the following: $|f(k,y)-f(k,\tilde y)| \leq \gamma(k)|y-\tilde y|, |f(k,y)| \leq \mu(k).$
$(y,\tilde {y})\in \mathbb {R}^d\times \mathbb {R}^d$, the following: $|f(k,y)-f(k,\tilde y)| \leq \gamma(k)|y-\tilde y|, |f(k,y)| \leq \mu(k).$![]()
2.1 Nonuniform dichotomies and Green's operator
In [Reference Dragičević, Zhang and Zhang11], the authors assume that the linear part has nonuniform strong exponential dichotomy on $\mathbb {Z}.$![]() For our purpose, we endow (2.1) to a more general nonautonomous hyperbolicity, which it satisfies on $\mathbb {Z}^+.$
For our purpose, we endow (2.1) to a more general nonautonomous hyperbolicity, which it satisfies on $\mathbb {Z}^+.$![]() Namely,
Namely,
(d1) System (2.1) has a nonuniform dichotomy, i.e. there are two invariant complementary projectors $P(\cdot )$
 and $Q(\cdot )$
and $Q(\cdot )$ such that $P(n)+Q(n)=I$
such that $P(n)+Q(n)=I$ for every $n\in \mathbb {Z}^+$
for every $n\in \mathbb {Z}^+$ , a nonnegative sequence $D$
, a nonnegative sequence $D$ and a strictly decreasing sequence convergent to zero $h$
and a strictly decreasing sequence convergent to zero $h$ with $h(0)=1$
with $h(0)=1$ such that
\[ \left\{\begin{array}{@{}ll} \left\Vert{\Phi(k,n)P(n)}\right\Vert \leq D(n) \left(\dfrac{h(k)}{h(n)}\right), & \forall\ k \geq n\geq 0 \\[9pt] \left\Vert{\Phi(k,n)Q(n)}\right\Vert \leq D(n) \left(\dfrac{h(n)}{h(k)}\right), & \forall\ 0\leq k\leq n, \end{array}\right. \]where $\Phi (k,n)$
such that
\[ \left\{\begin{array}{@{}ll} \left\Vert{\Phi(k,n)P(n)}\right\Vert \leq D(n) \left(\dfrac{h(k)}{h(n)}\right), & \forall\ k \geq n\geq 0 \\[9pt] \left\Vert{\Phi(k,n)Q(n)}\right\Vert \leq D(n) \left(\dfrac{h(n)}{h(k)}\right), & \forall\ 0\leq k\leq n, \end{array}\right. \]where $\Phi (k,n)$
 is the transition matrix for (2.1).
is the transition matrix for (2.1).
Remark 2.1 The transition matrix for (2.1) is the matrix function $\Phi :\mathbb {Z}^+\times \mathbb {Z}^+\to \mathcal {M}_{d\times d}(\mathbb {R})$![]() given by
given by

Remark 2.2 Projectors $P(\cdot )$![]() and $Q(\cdot )$
and $Q(\cdot )$![]() have been called invariant, which means they are under the assumption that for every $k,n\in \mathbb {Z}^+$
have been called invariant, which means they are under the assumption that for every $k,n\in \mathbb {Z}^+$![]() they satisfy
they satisfy
Remark 2.3 Green's operator for system (2.1) associated with the dichotomy (d1) is the matrix function $\mathcal {G}:\mathbb {Z}^+\times \mathbb {Z}^+\to \mathcal {M}_{d\times d}(\mathbb {R})$![]() given by
given by
Additionally it is easily deduced that for every $n\in \mathbb {Z}^+$![]() and every $k\neq n-1$
and every $k\neq n-1$![]()
The following properties establish a relation between Green's operator $\mathcal {G}$![]() associated with the dichotomy established in (d1) and the sequences $\mu$
associated with the dichotomy established in (d1) and the sequences $\mu$![]() and $\gamma.$
and $\gamma.$![]() These conditions are used in [Reference Castañeda, González and Robledo5] in order to obtain that (2.1) and (2.2) are topologically equivalent on $\mathbb {Z}^+$
These conditions are used in [Reference Castañeda, González and Robledo5] in order to obtain that (2.1) and (2.2) are topologically equivalent on $\mathbb {Z}^+$![]() .
.
(d2)
\[ \sum_{j=0}^{\infty}\Vert{\mathcal{G}(k,j+1)}\Vert \mu(j)<\infty\quad \text{for every }k\in \mathbb{Z}^+. \]
(d3)
\[ \sum_{j=0}^{\infty} \Vert{\mathcal{G}(k,j+1)}\Vert \gamma(j)\leq q<1\quad \text{for every }k \in \mathbb{Z}^+. \]
The property that we establish below has been used [Reference Castañeda, González and Robledo5] in order to ensure that solutions for system (2.2) can be uniquely backwards continued.
(d4) The sequence $\gamma$
 and the matrix function $A$
and the matrix function $A$ verify
\[ \Vert{A^{{-}1}(\ell)\gamma(\ell)}\Vert <1\quad \text{for every }\ell \in \mathbb{Z}^+. \]
verify
\[ \Vert{A^{{-}1}(\ell)\gamma(\ell)}\Vert <1\quad \text{for every }\ell \in \mathbb{Z}^+. \]
2.2 $C^r$ -topological equivalence on $\mathbb {Z}^+$
-topological equivalence on $\mathbb {Z}^+$
We recall the concept of topological equivalence for discrete systems.
Definition 2.4 Systems (2.1) and (2.2) are $\mathbb {Z}^+$![]() -topologically equivalent if there is a function $H:\mathbb {Z}^+\times \mathbb {R}^d\to \mathbb {R}^d$
-topologically equivalent if there is a function $H:\mathbb {Z}^+\times \mathbb {R}^d\to \mathbb {R}^d$![]() that satisfies:
that satisfies:
(i) If $x(k)$
 is a solution of (2.1), then $H[k,x(k)]$
is a solution of (2.1), then $H[k,x(k)]$ is a solution of (2.2).
is a solution of (2.2).(ii) $H(k,u)-u$
 is bounded over $\mathbb {Z}^+\times \mathbb {R}^d$
is bounded over $\mathbb {Z}^+\times \mathbb {R}^d$ .
.(iii) For each fixed $k\in \mathbb {Z}^+$
 , the map $u\mapsto H(k,u)$
, the map $u\mapsto H(k,u)$ is a homeomorphism of $\mathbb {R}^d$
is a homeomorphism of $\mathbb {R}^d$ .
.
Moreover, the function $u\mapsto G(k,u)=H^{-1}(k,u)$![]() satisfies (ii) and (iii) and maps solutions of (2.2) into solutions of (2.1).
satisfies (ii) and (iii) and maps solutions of (2.2) into solutions of (2.1).
As explained before, it can be interesting to study which properties can be deduced when studying the differentiability of such homeomorphisms. This idea motivates the following definition.
Definition 2.5 Systems (2.1) and (2.2) are $C^r$![]() -topologically equivalent on $\mathbb {Z}^+$
-topologically equivalent on $\mathbb {Z}^+$![]() if they are topologically equivalent on $\mathbb {Z}^+$
if they are topologically equivalent on $\mathbb {Z}^+$![]() and $u\mapsto H(k,u)$
and $u\mapsto H(k,u)$![]() is a diffeomorphism of class $C^r$
is a diffeomorphism of class $C^r$![]() , with $r\geq 1$
, with $r\geq 1$![]() for each fixed $k\in \mathbb {Z}^+$
for each fixed $k\in \mathbb {Z}^+$![]() .
.
The following result establishes a topological equivalence between systems (2.1) and (2.2). We highlight it, together with its proof, because it gives us the tools that will facilitate the presentation of our main results.
Proposition 2.6 [Reference Castañeda, González and Robledo5, theorem 2.1]
If conditions (d1)–(d4) hold, then systems (2.1) and (2.2) are $\mathbb {Z}^+$![]() -topologically equivalent.
-topologically equivalent.
To facilitate the reading of this article, we distinguish some relevant facts in the proof of theorem [Reference Castañeda, González and Robledo5, theorem 2.1]. Let us define

On the contrary, for each $(m,\xi )\in \mathbb {Z}^+\times \mathbb {R}^d$![]() we define the map $\Theta :\ell ^{\infty }(\mathbb {Z}^+,\mathbb {R}^d)\to \ell ^{\infty }(\mathbb {Z}^+,\mathbb {R}^d)$
we define the map $\Theta :\ell ^{\infty }(\mathbb {Z}^+,\mathbb {R}^d)\to \ell ^{\infty }(\mathbb {Z}^+,\mathbb {R}^d)$![]() given by
given by

Using Banach's fixed point theorem we conclude the existence of a unique fixed point

It is easily verified that this map is a solution for the initial value problem

By unicity of solutions we have
and analogously, we can verify
For every fixed $k\in \mathbb {Z}^+$![]() , consider the maps $H(k,\cdot ):\mathbb {R}^d\to \mathbb {R}^d$
, consider the maps $H(k,\cdot ):\mathbb {R}^d\to \mathbb {R}^d$![]() and $G(k,\cdot ):\mathbb {R}^d\to \mathbb {R}^d$
and $G(k,\cdot ):\mathbb {R}^d\to \mathbb {R}^d$![]() given by
given by

and

It has been proved that $H$![]() and $G=H^{-1}$
and $G=H^{-1}$![]() define the homeomorphisms that show the topological equivalence between (2.1) and (2.2), i.e.
define the homeomorphisms that show the topological equivalence between (2.1) and (2.2), i.e.
and
To study additional properties of $G$![]() , note that for $n< k$
, note that for $n< k$![]() we have
we have

which implies

In particular, for $n=0$![]() we have
we have

Hence, using the definition of $k\mapsto w^*(0;(k,\eta ))$![]() we conclude
we conclude

To prove the $C^r$![]() -topologically equivalence, in [Reference Castañeda, González and Robledo5] it is supposed that system (2.1) admits a nonuniform contraction, that is, in condition (d1) it is supposed that $P(\cdot ) = I_n.$
-topologically equivalence, in [Reference Castañeda, González and Robledo5] it is supposed that system (2.1) admits a nonuniform contraction, that is, in condition (d1) it is supposed that $P(\cdot ) = I_n.$![]() Namely, we have
Namely, we have
(D1) System (2.1) has a nonuniform dichotomy with projector $P(\cdot ) = I_n$
 , i.e. there exist a nonnegative sequence $D$
, i.e. there exist a nonnegative sequence $D$ and a monotone decreasing sequence convergent to zero $h$
and a monotone decreasing sequence convergent to zero $h$ , with $h(0)=1$
, with $h(0)=1$ , such that
\[ \Vert{\Phi(k,n)}\Vert \leq D(n)\frac{h(k)}{h(n)},\quad \forall\ k\geq n\geq 0. \]
, such that
\[ \Vert{\Phi(k,n)}\Vert \leq D(n)\frac{h(k)}{h(n)},\quad \forall\ k\geq n\geq 0. \]
Furthermore, if we consider the property
(d5) The map $u\mapsto f(k,u)$
 and its derivatives with respect to $u$
and its derivatives with respect to $u$ up to the order $r$
up to the order $r$ ($r\geq 1$
($r\geq 1$ ) are continuous functions of $(k,u)\in \mathbb {Z}^+\times \mathbb {R}^d$
) are continuous functions of $(k,u)\in \mathbb {Z}^+\times \mathbb {R}^d$ ,
,
we have the following result.
Proposition 2.7 [Reference Castañeda, González and Robledo5, lemma 2.3]
If conditions (D1), and (d2)–(d5) hold, then systems (2.1) and (2.2) are $C^r$![]() -topologically equivalent on $\mathbb {Z}^+$
-topologically equivalent on $\mathbb {Z}^+$![]() .
.
Remark 2.8 Note that when replacing (d1) with (D1), the form of Green's operator is simpler, hence conditions (d2) and (d3) are also considerably easier to handle. Also, in this case, the map $k\mapsto w^*(0;(k,\eta ))$![]() is identically zero, which allowed the authors to prove the differentiability of $u\mapsto G(k,u)$
is identically zero, which allowed the authors to prove the differentiability of $u\mapsto G(k,u)$![]() .
.
Remark 2.9 Note that (d4) and (d5) imply that the map $y\mapsto A(k)y+f(k,y)$![]() is invertible with $C^r$
is invertible with $C^r$![]() inverse for each $k\in \mathbb {Z}^+$
inverse for each $k\in \mathbb {Z}^+$![]() . Thus, we obtain that the map $\eta \mapsto y(0,k,\eta )$
. Thus, we obtain that the map $\eta \mapsto y(0,k,\eta )$![]() is $C^r$
is $C^r$![]() for every $k\in \mathbb {Z}^+$
for every $k\in \mathbb {Z}^+$![]() .
.
3. Diffeomorphism of discrete topological equivalence under a dichotomy
This section is devoted to study the differentiability properties of the topological equivalence. To obtain some class of differentiability we give sufficient conditions for this purpose: the first one will allow us to obtain that $G$![]() is of class $C^1$
is of class $C^1$![]() and $H$
and $H$![]() is differentiable except for a set of zero Lebesgue measure. The second condition helps to achieve $C^1$
is differentiable except for a set of zero Lebesgue measure. The second condition helps to achieve $C^1$![]() topological equivalence.
topological equivalence.
3.1 Almost $C^1$ topological equivalence
topological equivalence
The main goal of this subsection is to prove that $\eta \mapsto w^*(0;(m,\eta ))$![]() is of class $C^1$
is of class $C^1$![]() . Later, we show that $G$
. Later, we show that $G$![]() is of class $C^1$
is of class $C^1$![]() while $H$
while $H$![]() is almost everywhere differentiable. For this purpose, we consider the following property:
is almost everywhere differentiable. For this purpose, we consider the following property:
(d6) For each fixed $m\in \mathbb {Z}^+$
 , the sequences $D$
, the sequences $D$ , $h$
, $h$ and $\gamma$
and $\gamma$ satisfy
\[ \sum_{j=m+1}^{\infty}\left(D(j+1)h(j+1)\gamma(j) \left[\prod_{p=m}^{j-1} \Vert{A(p)}\Vert +\gamma(p)\right]\right)<{+}\infty. \]
satisfy
\[ \sum_{j=m+1}^{\infty}\left(D(j+1)h(j+1)\gamma(j) \left[\prod_{p=m}^{j-1} \Vert{A(p)}\Vert +\gamma(p)\right]\right)<{+}\infty. \]
Lemma 3.1 If conditions (d1)–(d6) hold, with $r=1$![]() on (d5), then $\eta \mapsto w^*(0;(m,\eta ))$
on (d5), then $\eta \mapsto w^*(0;(m,\eta ))$![]() is a differentiable map for every fixed $m\in \mathbb {Z}^+$
is a differentiable map for every fixed $m\in \mathbb {Z}^+$![]() .
.
Proof. Fix $\eta \in \mathbb {R}^d$![]() and let $(\delta _n)_{n\in \mathbb {N}}\subset \mathbb {R}^d$
and let $(\delta _n)_{n\in \mathbb {N}}\subset \mathbb {R}^d$![]() be a convergent to zero sequence such that $\delta _n\neq 0$
be a convergent to zero sequence such that $\delta _n\neq 0$![]() for every $n\in \mathbb {N}$
for every $n\in \mathbb {N}$![]() . Choose and fix $m\in \mathbb {Z}^+$
. Choose and fix $m\in \mathbb {Z}^+$![]() , we define
, we define

note that as $\eta \mapsto y(j,m,\eta )$![]() is continuous, then $\lim _{n\to \infty }y(j,m,\eta +\delta _n)=y(j,m,\eta )$
is continuous, then $\lim _{n\to \infty }y(j,m,\eta +\delta _n)=y(j,m,\eta )$![]() . Applying (d5), we have
. Applying (d5), we have
In the proof of proposition 2.6, in [Reference Castañeda, González and Robledo5, p. 11], the authors define for $j< m$![]()

and it is proved that
However, we know
hence
thus

For $j\geq m$![]() , we define $\mathcal {B}_m(m)=1$
, we define $\mathcal {B}_m(m)=1$![]() and
and

which, by (3.2), allows us to write for $j\geq m$![]()
Now, we define
hence, for every $j\in \mathbb {Z}^+$![]()
Thus,
Similarly,
Hence,

Besides, by using (d3) and (d6) we have

Finally, by using Lebesgue's dominated convergence theorem we obtain

which implies $\eta \mapsto w^*(0;(m,\eta ))$![]() is differentiable.
is differentiable.
Corollary 3.2 If conditions (d1)–(d6) hold, with $r=1$![]() on (d5), then for every $m\in \mathbb {Z}^+$
on (d5), then for every $m\in \mathbb {Z}^+$![]()

Moreover, $\eta \mapsto w^*(0;(m,\eta ))$![]() is a $C^1$
is a $C^1$![]() map for every fixed $m\in \mathbb {Z}^+$
map for every fixed $m\in \mathbb {Z}^+$![]() .
.
Proof. The identity is an immediate consequence of the previous lemma. From this identity and condition (d6), it follows easily, using Lebesgue's dominated convergence theorem, that $\eta \mapsto {\partial w^*(0;(m,\eta ))}/{\partial \eta }$![]() is continuous. Thus, $\eta \mapsto w^*(0;(m,\eta ))$
is continuous. Thus, $\eta \mapsto w^*(0;(m,\eta ))$![]() is a $C^1$
is a $C^1$![]() map.
map.
Corollary 3.3 If conditions (d1)–(d6) hold, with $r=1$![]() (d5), then for every $k\in \mathbb {Z}^+$
(d5), then for every $k\in \mathbb {Z}^+$![]() $\eta \mapsto G(k,\eta )$
$\eta \mapsto G(k,\eta )$![]() is a $C^1$
is a $C^1$![]() map. Moreover, for every fixed $k\in \mathbb {Z}^+$
map. Moreover, for every fixed $k\in \mathbb {Z}^+$![]() , $\xi \mapsto H(k,\xi )$
, $\xi \mapsto H(k,\xi )$![]() is almost everywhere differentiable, i.e. it is a differentiable map except for a set of zero Lebesgue measure.
is almost everywhere differentiable, i.e. it is a differentiable map except for a set of zero Lebesgue measure.
Proof. By proposition 2.6 we know that systems (2.1) and (2.2) are topologically equivalent. By lemma 3.1 and corollary 3.2, $\eta \mapsto w^*(0;(k,\eta ))$![]() is $C^1$
is $C^1$![]() differentiable for every $k\in \mathbb {Z}^+$
differentiable for every $k\in \mathbb {Z}^+$![]() , and as stated in remark 2.9, $\eta \mapsto y(0,k,\eta )$
, and as stated in remark 2.9, $\eta \mapsto y(0,k,\eta )$![]() is as well. Then (2.5) allows us to conclude $\eta \mapsto G(k,\eta )$
is as well. Then (2.5) allows us to conclude $\eta \mapsto G(k,\eta )$![]() is a $C^1$
is a $C^1$![]() map.
map.
For every $k \in \mathbb {Z}^+$![]() , let us call $\mathcal {N}_k:=\{\xi \in \mathbb {R}^d:\det ({\partial G}/{\partial \eta })(k,H(k,\xi ))=0\}$
, let us call $\mathcal {N}_k:=\{\xi \in \mathbb {R}^d:\det ({\partial G}/{\partial \eta })(k,H(k,\xi ))=0\}$![]() . We have $\mathcal {N}_k$
. We have $\mathcal {N}_k$![]() has zero Lebesgue measure by Sard's theorem and for every $\xi \not \in \mathcal {N}_k$
has zero Lebesgue measure by Sard's theorem and for every $\xi \not \in \mathcal {N}_k$![]() , as $G(k,H(k,\xi ))=\xi$
, as $G(k,H(k,\xi ))=\xi$![]() , we have
, we have
and so $({\partial H}/{\partial \xi })(k,\xi )=[({\partial G}/{\partial \eta })(k,H(k,\xi ))]^{-1},$![]() which completes the proof.
which completes the proof.
Corollary 3.4 Suppose system (2.1) admits a nonuniform exponential dichotomy, which means there are two complementary invariant projectors $P(\cdot )$![]() and $Q(\cdot )$
and $Q(\cdot )$![]() and constants $C,\lambda, \varepsilon >0$
and constants $C,\lambda, \varepsilon >0$![]() such that
such that

Furthermore, suppose that for every $k\in \mathbb {Z}^+$![]() $u\mapsto f(k,u)$
$u\mapsto f(k,u)$![]() is a $C^1$
is a $C^1$![]() function such that $u\mapsto ({\partial f}/{\partial u})(k,u)$
function such that $u\mapsto ({\partial f}/{\partial u})(k,u)$![]() is a bounded map that satisfies
is a bounded map that satisfies
and
for given $\nu,\kappa >0$![]() and $a\in (0,1)$
and $a\in (0,1)$![]() . Suppose also that $M\nu \,{\rm e}^{-\varepsilon }<1$
. Suppose also that $M\nu \,{\rm e}^{-\varepsilon }<1$![]() . Then, if ${aM\,{\rm e}^{-\lambda }<1}$
. Then, if ${aM\,{\rm e}^{-\lambda }<1}$![]() , for sufficiently small $\nu >0$
, for sufficiently small $\nu >0$![]() , $\eta \mapsto G(m,\eta )$
, $\eta \mapsto G(m,\eta )$![]() is a $C^1$
is a $C^1$![]() map and $\xi \mapsto H(m,\xi )$
map and $\xi \mapsto H(m,\xi )$![]() is almost everywhere differentiable.
is almost everywhere differentiable.
Proof. Condition (d1) is easily verified with $D(n)=C\,{\rm e}^{\varepsilon n}$![]() and $h(n)={\rm e}^{-\lambda n}$
and $h(n)={\rm e}^{-\lambda n}$![]() . It is easy to see that condition (3.8) implies that
. It is easy to see that condition (3.8) implies that
so $\gamma (k)=\nu \,{\rm e}^{-\varepsilon (k+1)}a^k$![]() and $\mu (k)=\kappa \,{\rm e}^{-\varepsilon (k+1)}$
and $\mu (k)=\kappa \,{\rm e}^{-\varepsilon (k+1)}$![]() . Hence condition (d2) is immediately satisfied and, provided $\nu$
. Hence condition (d2) is immediately satisfied and, provided $\nu$![]() is sufficiently small, so is (d3). Note that
is sufficiently small, so is (d3). Note that
thus condition (d4) is verified. Condition (d5) is satisfied by hypothesis, with $r=1$![]() . Now consider the map $j\mapsto \mathcal {B}_m(j)$
. Now consider the map $j\mapsto \mathcal {B}_m(j)$![]() defined in (3.3). It is easy to see that for $j\geq m$
defined in (3.3). It is easy to see that for $j\geq m$![]() we have
we have
thus

which, as $aM\,{\rm e}^{-\lambda }<1$![]() , is finite provided $\nu$
, is finite provided $\nu$![]() is sufficiently small, so condition (d6) is satisfied. Applying corollary 3.3, the statement is verified.
is sufficiently small, so condition (d6) is satisfied. Applying corollary 3.3, the statement is verified.
Remark 3.5 In the previous corollary, if we allow $\varepsilon =0$![]() , we recover the classic exponential dichotomy. Furthermore, we would like to impose weaker conditions, in particular $M\,{\rm e}^{-\lambda }<1$
, we recover the classic exponential dichotomy. Furthermore, we would like to impose weaker conditions, in particular $M\,{\rm e}^{-\lambda }<1$![]() , and hence $a=1$
, and hence $a=1$![]() , but it is a well-known fact in literature that this is impossible for both the exponential and nonuniform exponential dichotomies, since for both cases in general we have $M\,{\rm e}^{-\lambda }\geq 1$
, but it is a well-known fact in literature that this is impossible for both the exponential and nonuniform exponential dichotomies, since for both cases in general we have $M\,{\rm e}^{-\lambda }\geq 1$![]() [Reference Shi and Xiong19, p. 823]. Nevertheless, note that given any linear system (2.1), a wide family of perturbations $f$
[Reference Shi and Xiong19, p. 823]. Nevertheless, note that given any linear system (2.1), a wide family of perturbations $f$![]() can be found such that $M\nu \,{\rm e}^{-\varepsilon }<1$
can be found such that $M\nu \,{\rm e}^{-\varepsilon }<1$![]() and $aM\,{\rm e}^{-\lambda }<1$
and $aM\,{\rm e}^{-\lambda }<1$![]() , since both inequalities can be achieved by setting $f$
, since both inequalities can be achieved by setting $f$![]() small enough and with a fast enough decreasing rate.
small enough and with a fast enough decreasing rate.
Remark 3.6 Corollary 3.4 has been inspired by [Reference Dragičević, Zhang and Zhang11, theorem 2]. Our approach and that result consider (3.8), the same dichotomy and both results work for $\nu$![]() sufficiently small. Nevertheless, we imposed the extra hypothesis $aM\,{\rm e}^{-\lambda }<1$
sufficiently small. Nevertheless, we imposed the extra hypothesis $aM\,{\rm e}^{-\lambda }<1$![]() and conditions (3.7) and (d4).
and conditions (3.7) and (d4).
Moreover, our result gives topologically equivalence on $\mathbb {Z}^+$![]() with maps such that $\eta \mapsto G(m,\eta )$
with maps such that $\eta \mapsto G(m,\eta )$![]() is a $C^1$
is a $C^1$![]() map and $\xi \mapsto H(m,\xi )$
map and $\xi \mapsto H(m,\xi )$![]() is almost everywhere differentiable, in contrast to the mentioned theorem, which gives $C^1$
is almost everywhere differentiable, in contrast to the mentioned theorem, which gives $C^1$![]() -topologically equivalence on $\mathbb {Z}$
-topologically equivalence on $\mathbb {Z}$![]() . However, our approach does not impose a Lipschitz condition for the derivative of the perturbation, neither relies on spectral properties of the dichotomy, which is the core of that result.
. However, our approach does not impose a Lipschitz condition for the derivative of the perturbation, neither relies on spectral properties of the dichotomy, which is the core of that result.
3.2 Examples
This subsection is devoted to give examples that allow us to show different ways to obtain the conditions in corollary 3.3.
Example 3.7 Let $(a_n)_{n\in \mathbb {N}},(b_n)_{n\in \mathbb {N}},(c_n)_{n\in \mathbb {N}}$![]() three sequences such that
three sequences such that
for given $M,\alpha >0$![]() , and let $(c_n)_{n\in \mathbb {N}}$
, and let $(c_n)_{n\in \mathbb {N}}$![]() be monotone nondecreasing. Consider $A(n)\in \mathcal {M}_{3\times 3}(\mathbb {R})$
be monotone nondecreasing. Consider $A(n)\in \mathcal {M}_{3\times 3}(\mathbb {R})$![]() the diagonal matrix given by
the diagonal matrix given by

and consider system (2.1) associated with this sequence of matrices. Let $(r_n)_{n\in \mathbb {N}}$![]() be a summable nonnegative sequence and define $(\gamma _n)_{n\in \mathbb {N}}$
be a summable nonnegative sequence and define $(\gamma _n)_{n\in \mathbb {N}}$![]() the sequence given by
the sequence given by
Let $g:\mathbb {R}^3\to \mathbb {R}^3$![]() be a bounded, differentiable Lipschitz (with constant $\leq 1$
be a bounded, differentiable Lipschitz (with constant $\leq 1$![]() ) map, define $f:\mathbb {Z}^+\times \mathbb {R}^3\to \mathbb {R}^3$
) map, define $f:\mathbb {Z}^+\times \mathbb {R}^3\to \mathbb {R}^3$![]() given by $f(k,x)=\gamma _kg(x)$
given by $f(k,x)=\gamma _kg(x)$![]() and consider system (2.2) associated with this perturbation and the previous linear system. Then, if $M r_n<\alpha$
and consider system (2.2) associated with this perturbation and the previous linear system. Then, if $M r_n<\alpha$![]() for every $n\in \mathbb {N}$
for every $n\in \mathbb {N}$![]() and
and

systems (2.1) and (2.2) are topologically equivalent on $\mathbb {Z}^+$![]() . Moreover, for every $k\in \mathbb {Z}^+$
. Moreover, for every $k\in \mathbb {Z}^+$![]() , $\eta \mapsto G(k,\eta )$
, $\eta \mapsto G(k,\eta )$![]() is a $C^1$
is a $C^1$![]() map and $\xi \mapsto H(k,\xi )$
map and $\xi \mapsto H(k,\xi )$![]() is almost everywhere differentiable.
is almost everywhere differentiable.
In fact, since $0\leq a_n,b_n\leq c_n$![]() , then $ \Vert{A(n)}\Vert =c_n\leq M$
, then $ \Vert{A(n)}\Vert =c_n\leq M$![]() and $ \Vert{A^{-1}(n)}\Vert\leq \alpha ^{-1}$
and $ \Vert{A^{-1}(n)}\Vert\leq \alpha ^{-1}$![]() . Furthermore, let $P(\cdot )$
. Furthermore, let $P(\cdot )$![]() and $Q(\cdot )$
and $Q(\cdot )$![]() be
be

Then, if we consider $\Phi (m,n)$![]() be the transition matrix for (2.1), it is clear that
be the transition matrix for (2.1), it is clear that

Hence, setting $h(n)=\prod _{p=1}^{n-1}c_p^{-1}$![]() and $D(n)=1$
and $D(n)=1$![]() , condition (d1) follows. Note also
, condition (d1) follows. Note also
thus (d4) is verified. It is easy to inductively prove

Note that for every $k\in \mathbb {Z}^+$![]() we have
we have

hence conditions (d3) and (d2) are satisfied with $\mu _j=\gamma _j \Vert{g}\Vert_\infty$![]() . Thus, applying proposition 2.6 it follows that the systems are topologically equivalent on $\mathbb {Z}^+$
. Thus, applying proposition 2.6 it follows that the systems are topologically equivalent on $\mathbb {Z}^+$![]() .
.
Condition (d5) is verified by hypothesis. Now, recall the map $j\mapsto \mathcal {B}_m(j)$![]() defined in (3.3). It is easy to see $m\geq n$
defined in (3.3). It is easy to see $m\geq n$![]() implies $\mathcal {B}_m(j)\leq \mathcal {B}_n(j)$
implies $\mathcal {B}_m(j)\leq \mathcal {B}_n(j)$![]() , hence for a fixed $m\in \mathbb {Z}^+$
, hence for a fixed $m\in \mathbb {Z}^+$![]()

So, we have

Hence, (d6) is fulfilled. Finally, applying corollary 3.3, we show our claim.
Remark 3.8 Condition $\sup _{k\in \mathbb {Z}^+}({c_{k-1}r_{k-1}}/{(r_{k-2}+r_{k-3}+\cdots +1)})+\sum _{j=1, j\neq k-1}^\infty r_j<1$![]() is obtained, for example, if the increasing rate of $(c_n)$
is obtained, for example, if the increasing rate of $(c_n)$![]() is smaller than the growing rate of the partial sums of $(r_n)$
is smaller than the growing rate of the partial sums of $(r_n)$![]() and $ \Vert{r}\Vert_1<1$
and $ \Vert{r}\Vert_1<1$![]() . Another simpler case is if $M \Vert{r}\Vert_1<1$
. Another simpler case is if $M \Vert{r}\Vert_1<1$![]() .
.
Example 3.9 Let $(a_n)_{n\in \mathbb {N}},(b_n)_{n\in \mathbb {N}},(c_n)_{n\in \mathbb {N}}$![]() three sequences as in (3.9), $A(n)$
three sequences as in (3.9), $A(n)$![]() as in (3.10) and system (2.1) associated with this sequence of matrices. Let $(r_n)_{n\in \mathbb {N}}$
as in (3.10) and system (2.1) associated with this sequence of matrices. Let $(r_n)_{n\in \mathbb {N}}$![]() be a summable nonnegative sequence and define $(\gamma _n)_{n\in \mathbb {N}}$
be a summable nonnegative sequence and define $(\gamma _n)_{n\in \mathbb {N}}$![]() the sequence given by
the sequence given by
Let $g:\mathbb {R}^3\to \mathbb {R}^3$![]() be a bounded, differentiable Lipschitz (with constant $\leq 1$
be a bounded, differentiable Lipschitz (with constant $\leq 1$![]() ) map, define $f:\mathbb {Z}^+\times \mathbb {R}^3\to \mathbb {R}^3$
) map, define $f:\mathbb {Z}^+\times \mathbb {R}^3\to \mathbb {R}^3$![]() given by $f(k,x)=\gamma _kg(x)$
given by $f(k,x)=\gamma _kg(x)$![]() and consider system (2.2) associated with this perturbation and the previous linear system. Then, if $r_n<\alpha$
and consider system (2.2) associated with this perturbation and the previous linear system. Then, if $r_n<\alpha$![]() for every $n\in \mathbb {N}$
for every $n\in \mathbb {N}$![]() and $ \Vert{r}\Vert_1<1$
and $ \Vert{r}\Vert_1<1$![]() , systems (2.1) and (2.2) are topologically equivalent on $\mathbb {Z}^+$
, systems (2.1) and (2.2) are topologically equivalent on $\mathbb {Z}^+$![]() . Moreover, for every $k\in \mathbb {Z}^+$
. Moreover, for every $k\in \mathbb {Z}^+$![]() , $\eta \mapsto G(k,\eta )$
, $\eta \mapsto G(k,\eta )$![]() is a $C^1$
is a $C^1$![]() map and $\xi \mapsto H(k,\xi )$
map and $\xi \mapsto H(k,\xi )$![]() is almost everywhere differentiable.
is almost everywhere differentiable.
Indeed, conditions (d1), (d4) and (d5) follow easily in the same fashion as in the previous example, with $P(\cdot )$![]() and $Q(\cdot )$
and $Q(\cdot )$![]() as in (3.11). It is easy to inductively prove
as in (3.11). It is easy to inductively prove

Note that for a fixed $k\in \mathbb {Z}^+$![]()

hence proving (d3) and (d2) with $\mu _j=\gamma _j \Vert{g}\Vert_\infty$![]() . Thus, by proposition 2.6 the systems are topologically equivalent on $\mathbb {Z}^+$
. Thus, by proposition 2.6 the systems are topologically equivalent on $\mathbb {Z}^+$![]() . Now, for a fixed $m\in \mathbb {Z}^+$
. Now, for a fixed $m\in \mathbb {Z}^+$![]() we have
we have

Hence, (d6) is fulfilled. Thus, applying corollary 3.3 our claim is proved.
3.3 $C^1$ topological equivalence
topological equivalence
We show, in this subsection, that the topological equivalence between systems (2.1) and (2.2) is of class $C^1.$![]() Moreover, we prove that the derivatives of $G(k,\xi )$
Moreover, we prove that the derivatives of $G(k,\xi )$![]() and $H(k,\xi )$
and $H(k,\xi )$![]() are bounded as a function of $\xi$
are bounded as a function of $\xi$![]() variable for each fixed $k.$
variable for each fixed $k.$![]() To obtain our main result, we introduce the following condition:
To obtain our main result, we introduce the following condition:
(d7) For each fixed $m\in \mathbb {Z}^+$
 , the map $j\mapsto \mathcal {A}_m(j)$
, the map $j\mapsto \mathcal {A}_m(j)$ defined in (3.5) verifies
\[ \sum_{j = 0}^{\infty} \Vert{\mathcal{G}(m,j+1)}\Vert \gamma(j)\mathcal{A}_m(j)<1. \]
defined in (3.5) verifies
\[ \sum_{j = 0}^{\infty} \Vert{\mathcal{G}(m,j+1)}\Vert \gamma(j)\mathcal{A}_m(j)<1. \]
Remark 3.10 To the best of our knowledge, condition (d7) first appeared in [Reference Backes and Dragičević1], when Backes and Dragičević were also studying the smooth linearization of nonautonomous systems without spectral conditions to analyse coupled systems.
Lemma 3.11 If conditions (d1)–(d7) hold, with $r=1$![]() on (d5), then $\eta \mapsto w^*(m;(m,\eta ))$
on (d5), then $\eta \mapsto w^*(m;(m,\eta ))$![]() is a $C^1$
is a $C^1$![]() map for every $m\in \mathbb {Z}^+$
map for every $m\in \mathbb {Z}^+$![]() . Moreover, in that case we have
. Moreover, in that case we have

and
Note that the proof of this lemma follows in the same fashion as lemma 3.1 and corollary 3.2. Moreover, statement (3.12) is a direct consequence of condition (d7).
Now we can establish the main result of this section.
Theorem 3.12 If conditions (d1)–(d7) hold, with $r=1$![]() on (d5), then systems (2.1) and (2.2) are $C^1$
on (d5), then systems (2.1) and (2.2) are $C^1$![]() -topologically equivalent on $\mathbb {Z}^+$
-topologically equivalent on $\mathbb {Z}^+$![]() . Moreover, in this case both $\xi \mapsto H_\xi (m,\xi )$
. Moreover, in this case both $\xi \mapsto H_\xi (m,\xi )$![]() and $\eta \mapsto G_\eta (m,\eta )$
and $\eta \mapsto G_\eta (m,\eta )$![]() are bounded maps for every fixed $m\in \mathbb {Z}^+$
are bounded maps for every fixed $m\in \mathbb {Z}^+$![]() .
.
Proof. It is enough to note that $\eta \mapsto G(m,\eta )=\eta +w^*(m;(m,\eta ))$![]() is differentiable, and as the norm of the derivative of $w^*(m;(m,\eta ))$
is differentiable, and as the norm of the derivative of $w^*(m;(m,\eta ))$![]() , by lemma 3.11, is smaller than 1, then the derivative of $G(m,\eta )$
, by lemma 3.11, is smaller than 1, then the derivative of $G(m,\eta )$![]() is invertible everywhere. Moreover, as $G(m,\eta )-\eta$
is invertible everywhere. Moreover, as $G(m,\eta )-\eta$![]() is bounded, thus $G(m,\eta )\to \infty$
is bounded, thus $G(m,\eta )\to \infty$![]() when $|\eta |\to \infty$
when $|\eta |\to \infty$![]() . Hence, by [Reference Plastock16, corollary 2.1], $\xi \mapsto G(m,\xi )$
. Hence, by [Reference Plastock16, corollary 2.1], $\xi \mapsto G(m,\xi )$![]() is a $C^1$
is a $C^1$![]() diffeomorphism. In particular, $\xi \mapsto H(m,\xi )$
diffeomorphism. In particular, $\xi \mapsto H(m,\xi )$![]() is also differentiable.
is also differentiable.
Now, observe that
thus, under condition (d7) it is easy to see
On the other hand, observe that as

then, using (2.3) we obtain
Thus,

and, using (2.4), we conclude

Now, observe

Hence, by using (d7)

Remark 3.13 Suppose all conditions from corollary 3.4 are verified. By theorem 3.12, it is enough to verify condition (d7) in order to have that (2.1) and (2.2) are $C^1$![]() -topologically equivalent on $\mathbb {Z}^+$
-topologically equivalent on $\mathbb {Z}^+$![]() . Now, assume we can find a linear system (2.1) such that $M\,{\rm e}^{-\lambda +\varepsilon }<{\rm e}^{\varepsilon }$
. Now, assume we can find a linear system (2.1) such that $M\,{\rm e}^{-\lambda +\varepsilon }<{\rm e}^{\varepsilon }$![]() . It is easy to see that we can obtain a family of perturbations $f$
. It is easy to see that we can obtain a family of perturbations $f$![]() such that:
such that:
• $M\,{\rm e}^{-\lambda +\varepsilon }<{\rm e}^{\varepsilon }-M\nu$
 ,
,• denoting $b={M\,{\rm e}^{-\lambda }}/{a(1-M\nu \,{\rm e}^{-\varepsilon })}$
 , it is also verified
\[ C\nu\left(\frac{M}{|M{\rm e}^{-\lambda}-a(1-M\nu \,{\rm e}^{-\varepsilon})|}+ {\rm e}^{-\lambda}+\frac{{\rm e}^{{-}2\lambda}a(M+\nu \,{\rm e}^{-\varepsilon})}{1-a\,{\rm e}^{-\lambda}(M+\nu \,{\rm e}^{-\varepsilon})}\right)<1,\enspace \text{if }b\neq 1, \]or
, it is also verified
\[ C\nu\left(\frac{M}{|M{\rm e}^{-\lambda}-a(1-M\nu \,{\rm e}^{-\varepsilon})|}+ {\rm e}^{-\lambda}+\frac{{\rm e}^{{-}2\lambda}a(M+\nu \,{\rm e}^{-\varepsilon})}{1-a\,{\rm e}^{-\lambda}(M+\nu \,{\rm e}^{-\varepsilon})}\right)<1,\enspace \text{if }b\neq 1, \]or \[ C\nu\left({\rm e}^\lambda \sup_{m\in \mathbb{Z}^+}ma^m+ {\rm e}^{-\lambda}+\frac{{\rm e}^{{-}2\lambda}a(M+\nu \,{\rm e}^{-\varepsilon})}{1-a\,{\rm e}^{-\lambda}(M+\nu \,{\rm e}^{-\varepsilon})}\right)<1,\quad \text{if }b= 1, \]
\[ C\nu\left({\rm e}^\lambda \sup_{m\in \mathbb{Z}^+}ma^m+ {\rm e}^{-\lambda}+\frac{{\rm e}^{{-}2\lambda}a(M+\nu \,{\rm e}^{-\varepsilon})}{1-a\,{\rm e}^{-\lambda}(M+\nu \,{\rm e}^{-\varepsilon})}\right)<1,\quad \text{if }b= 1, \]
since both these conditions can easily be achieved for small enough $\nu >0$![]() .
.
Under these conditions, it is easy to prove $b>0$![]() and $ab<1$
and $ab<1$![]() . Then, considering $j\mapsto \mathcal {C}_m(j)$
. Then, considering $j\mapsto \mathcal {C}_m(j)$![]() as defined in (3.1), for $j< m$
as defined in (3.1), for $j< m$![]() we have
we have
hence,

Thus, if $b\neq 1$![]() , we have
, we have

and if $b=1$![]() , we have
, we have

Thus, under these hypotheses, condition (d7) is verified. However, as mentioned in remark 3.5, it is impossible to find a linear system (2.1) such that $M\,{\rm e}^{-\lambda +\varepsilon }<{\rm e}^\varepsilon$![]() . In other words, using the tools developed in this study, theorem 3.12 fails to be applicable to the exponential or nonuniform exponential case; the latter dichotomy is the one considered in corollary 3.4.
. In other words, using the tools developed in this study, theorem 3.12 fails to be applicable to the exponential or nonuniform exponential case; the latter dichotomy is the one considered in corollary 3.4.
4. Second derivative
We once again consider expression (2.5) in order to study the second derivative of the homeomorphism of topological equivalence. Taking into account remark 2.9, the map $\eta \mapsto y(0,m,\eta )$![]() is of class $C^r$
is of class $C^r$![]() ($r\geq 1$
($r\geq 1$![]() ) for every fixed $m \in \mathbb {Z}^+$
) for every fixed $m \in \mathbb {Z}^+$![]() if conditions (d1)–(d5) are satisfied; hence the class of differentiability of the homeomorphism relies on the differentiability of the maps $\eta \mapsto w^*(0;(m,\eta ))$
if conditions (d1)–(d5) are satisfied; hence the class of differentiability of the homeomorphism relies on the differentiability of the maps $\eta \mapsto w^*(0;(m,\eta ))$![]() and $\eta \mapsto w^*(m;(m,\eta ))$
and $\eta \mapsto w^*(m;(m,\eta ))$![]() .
.
Lemma 4.1 Suppose conditions (d1)–(d6) hold, and (d5) is fulfilled with $r=2$![]() . Also, there are functions $\Gamma :\mathbb {Z}^+\to \mathbb {R}^+$
. Also, there are functions $\Gamma :\mathbb {Z}^+\to \mathbb {R}^+$![]() and $\pi _m:\mathbb {Z}^+\to \mathbb {R}^+$
and $\pi _m:\mathbb {Z}^+\to \mathbb {R}^+$![]() such that
such that

and

Finally, suppose that for each fixed $m\in \mathbb {Z}^+$![]() , the sequences satisfy
, the sequences satisfy

Then $\eta \mapsto w^*(0;(m,\eta ))$![]() is a $C^2$
is a $C^2$![]() map.
map.
Proof. By corollary 3.2 we have

for every fixed $m\in \mathbb {Z}^+$![]() . Hence, in order to prove the differentiability of this map, it is enough to find a summable function that uniformly (with respect to $\eta$
. Hence, in order to prove the differentiability of this map, it is enough to find a summable function that uniformly (with respect to $\eta$![]() ) dominates
) dominates

for every $j\geq 0$![]() , which is verified by hypothesis. Therefore, we apply the same strategy as in the proof of lemma 3.1 and corollary 3.2.
, which is verified by hypothesis. Therefore, we apply the same strategy as in the proof of lemma 3.1 and corollary 3.2.
Corollary 4.2 If conditions (d1)–(d6) hold, and (d5) is satisfied with $r=2$![]() , and conditions of lemma 4.1 are satisfied, then $\eta \mapsto G(k,\eta )$
, and conditions of lemma 4.1 are satisfied, then $\eta \mapsto G(k,\eta )$![]() is a $C^2$
is a $C^2$![]() map for every $k\in \mathbb {Z}^+$
map for every $k\in \mathbb {Z}^+$![]() . Moreover, for every fixed $k\in \mathbb {Z}^+$
. Moreover, for every fixed $k\in \mathbb {Z}^+$![]() , $\xi \mapsto H(k,\xi )$
, $\xi \mapsto H(k,\xi )$![]() is almost everywhere two times differentiable, i.e. it is a map two times differentiable except for a set of zero Lebesgue measure.
is almost everywhere two times differentiable, i.e. it is a map two times differentiable except for a set of zero Lebesgue measure.
Note that corollary 4.2 follows easily in the same fashion as the proof of corollary 3.3. Actually, for a fixed $k\in \mathbb {Z}^+$![]() , it can be deduced that outside of the set of zero Lebesgue measure $\mathcal {N}_k$
, it can be deduced that outside of the set of zero Lebesgue measure $\mathcal {N}_k$![]() (defined in the proof of corollary 3.3) where $\xi \mapsto H(k,\xi )$
(defined in the proof of corollary 3.3) where $\xi \mapsto H(k,\xi )$![]() is not differentiable, $\xi \mapsto H(k,\xi )$
is not differentiable, $\xi \mapsto H(k,\xi )$![]() is two times differentiable.
is two times differentiable.
Now we can establish the main result of this section.
Theorem 4.3 If conditions (d1)–(d7), with $r=2$![]() on (d5), and conditions from lemma 4.1 hold, then systems (2.1) and (2.2) are $C^2$
on (d5), and conditions from lemma 4.1 hold, then systems (2.1) and (2.2) are $C^2$![]() -topologically equivalent on $\mathbb {R}^+$
-topologically equivalent on $\mathbb {R}^+$![]() . Moreover, in this case both $\xi \mapsto H_\xi (m,\xi )$
. Moreover, in this case both $\xi \mapsto H_\xi (m,\xi )$![]() and $\eta \mapsto G_\eta (m,\eta )$
and $\eta \mapsto G_\eta (m,\eta )$![]() are bounded maps for every fixed $m\in \mathbb {Z}^+$
are bounded maps for every fixed $m\in \mathbb {Z}^+$![]() .
.
Proof. By lemma 4.1 $\eta \mapsto w^*(0;(k,\eta ))$![]() is a $C^2$
is a $C^2$![]() map, thus using (2.5) we can deduce $\eta \mapsto G(k,\eta )$
map, thus using (2.5) we can deduce $\eta \mapsto G(k,\eta )$![]() is a $C^2$
is a $C^2$![]() map. Now, observe that as $G(k,H(k,\xi ))=\xi$
map. Now, observe that as $G(k,H(k,\xi ))=\xi$![]() , and by theorem 3.12 both $G(k,\cdot )$
, and by theorem 3.12 both $G(k,\cdot )$![]() and $H(k,\cdot )$
and $H(k,\cdot )$![]() are $C^1$
are $C^1$![]() maps, then
maps, then
thus
hence,
which is valid, since, as stated before, under condition (d7) the first derivative of $G(k,\cdot )$![]() is invertible everywhere. Furthermore, both $\xi \mapsto H_{\xi }(k,\xi )$
is invertible everywhere. Furthermore, both $\xi \mapsto H_{\xi }(k,\xi )$![]() and $\eta \mapsto G_{\eta }(k,\eta )$
and $\eta \mapsto G_{\eta }(k,\eta )$![]() are bounded maps for every $k\in \mathbb {Z}^+$
are bounded maps for every $k\in \mathbb {Z}^+$![]() , such as in theorem 3.12.
, such as in theorem 3.12.
Now we proceed to study some technical results in order to establish a concrete example of corollary 4.2.
Lemma 4.4 Suppose conditions (d4)–(d5) hold, with $r=2$![]() on (d5). Furthermore, suppose there exist a function $\Gamma :\mathbb {Z}^+\to \mathbb {R}^+$
on (d5). Furthermore, suppose there exist a function $\Gamma :\mathbb {Z}^+\to \mathbb {R}^+$![]() that verifies (4.1). Then, for every $j\geq m$
that verifies (4.1). Then, for every $j\geq m$![]()

Proof. Fix $m\in \mathbb {Z}^+$![]() . We know $\eta \mapsto ({\partial y}/{\partial \eta })(j,m,\eta )$
. We know $\eta \mapsto ({\partial y}/{\partial \eta })(j,m,\eta )$![]() is well defined for every $j\geq m$
is well defined for every $j\geq m$![]() . Consider the matrix initial value problem:
. Consider the matrix initial value problem:

From the proof of theorem 2.7 we can deduce $j\mapsto z(j,m,\eta )=({\partial y}/{\partial \eta })(j,m,\eta )$![]() is solution of (4.4), hence,
is solution of (4.4), hence,
Then, we obtain
or equivalently
Now, set $\hat {m}\geq m+1$![]() . Note that
. Note that

from where it follows that

hence, using (3.4) and (3.6), we obtain

Thus, defining for $j\geq 1$![]()

and

we have $\phi _{1,m}\leq \Gamma (m)$![]() and
and
Thus, defining $\beta _{0,m}=\Gamma (m)$![]() it is easy to inductively prove
it is easy to inductively prove

and as $z(j,m,\eta )=({\partial y}/{\partial \eta })(j,m,\eta )$![]() , this implies that for every $j\geq m$
, this implies that for every $j\geq m$![]()

Corollary 4.5 Suppose conditions (d4)–(d5) hold, with $r=2$![]() on (d5). If $\gamma (j)=\nu \,{\rm e}^{-\varepsilon (j+1)}a^j$
on (d5). If $\gamma (j)=\nu \,{\rm e}^{-\varepsilon (j+1)}a^j$![]() and $\Gamma (j)=\zeta \,{\rm e}^{-\varepsilon (j+1)}a^j$
and $\Gamma (j)=\zeta \,{\rm e}^{-\varepsilon (j+1)}a^j$![]() satisfies (4.1), then if $a(M+\nu )<{\rm e}^{\varepsilon }$
satisfies (4.1), then if $a(M+\nu )<{\rm e}^{\varepsilon }$![]() , for every $j\geq m$
, for every $j\geq m$![]()

Proof. Applying lemma 4.4 and noticing $ \Vert{A(p)}\Vert +\gamma (p)\leq M+\nu$![]() for every $p\in \mathbb {Z}^+$
for every $p\in \mathbb {Z}^+$![]() , we have
, we have

Theorem 4.6 Suppose system (2.1) admits a nonuniform exponential dichotomy, which means there are two complementary invariant projectors $P(\cdot )$![]() and $Q(\cdot )$
and $Q(\cdot )$![]() and constants $C,\lambda, \varepsilon >0$
and constants $C,\lambda, \varepsilon >0$![]() such that
such that

Furthermore, suppose that for every $k\in \mathbb {Z}^+$![]() $u\mapsto f(k,u)$
$u\mapsto f(k,u)$![]() is a $C^2$
is a $C^2$![]() function such that:
function such that:

and
for given $\kappa,\nu,\zeta >0$![]() and $a\in (0,1)$
and $a\in (0,1)$![]() . Suppose also that $M\nu \,{\rm e}^{-\varepsilon }<1$
. Suppose also that $M\nu \,{\rm e}^{-\varepsilon }<1$![]() and $a(M+\nu )<{\rm e}^{\varepsilon }$
and $a(M+\nu )<{\rm e}^{\varepsilon }$![]() . Then, if $aM^2\,{\rm e}^{-\lambda }<1$
. Then, if $aM^2\,{\rm e}^{-\lambda }<1$![]() , for sufficiently small $\nu >0$
, for sufficiently small $\nu >0$![]() , $\eta \mapsto G(k,\eta )$
, $\eta \mapsto G(k,\eta )$![]() is a $C^2$
is a $C^2$![]() map and $\xi \mapsto H(k,\xi )$
map and $\xi \mapsto H(k,\xi )$![]() is almost everywhere two times differentiable for every fixed $k\in \mathbb {Z}^+$
is almost everywhere two times differentiable for every fixed $k\in \mathbb {Z}^+$![]() .
.
Proof. By corollary 3.4 we know conditions (d1)–(d6) are satisfied, since $aM^2\,{\rm e}^{-\lambda }>aM\,{\rm e}^{-\lambda }$![]() . In particular, (d3) is verified with $\gamma (j)=\nu \,{\rm e}^{-\varepsilon (j+1)}a^j$
. In particular, (d3) is verified with $\gamma (j)=\nu \,{\rm e}^{-\varepsilon (j+1)}a^j$![]() and (d5) is satisfied with $r=2$
and (d5) is satisfied with $r=2$![]() .
.
It is easy to see that (4.5) implies (4.1) from lemma 4.1 with $\Gamma (j)=\zeta \,{\rm e}^{-\varepsilon (j+1)}a^j$![]() . Once again consider the map $j\mapsto \mathcal {B}_m(j)$
. Once again consider the map $j\mapsto \mathcal {B}_m(j)$![]() defined in (3.3). As in the proof of corollary 3.4, it is easy to see for $j\geq m$
defined in (3.3). As in the proof of corollary 3.4, it is easy to see for $j\geq m$![]() :
:
Hence,

As $aM^2{\rm e}^{-\lambda }<1$![]() , then for small enough $\nu$
, then for small enough $\nu$![]() we have
we have

On the other hand, using corollary 4.5 we have

for every $j\geq m$![]() , thus
, thus

for a small enough $\nu$![]() , where $K_m={C \nu \zeta ({\rm e}^{-\varepsilon }a)^m\,{\rm e}^{-\lambda }}{{\rm e}^{\varepsilon }(M+\nu )-a(M+\nu )^2}$
, where $K_m={C \nu \zeta ({\rm e}^{-\varepsilon }a)^m\,{\rm e}^{-\lambda }}{{\rm e}^{\varepsilon }(M+\nu )-a(M+\nu )^2}$![]() . Thus, the previous expression along with (4.6) implies condition (4.3) from lemma 4.1. Hence, applying corollary 4.2 the theorem follows.
. Thus, the previous expression along with (4.6) implies condition (4.3) from lemma 4.1. Hence, applying corollary 4.2 the theorem follows.
Remark 4.7 This theorem extends corollary 3.4, with some extra hypothesis. Note that we impose the existence of a function $\Gamma$![]() that satisfies (4.1). This implies a Lipschitz condition for ${\partial f}/{\partial u}$
that satisfies (4.1). This implies a Lipschitz condition for ${\partial f}/{\partial u}$![]() , which, as mentioned in remark 3.6, was used by the authors in [Reference Dragičević, Zhang and Zhang11] in order to prove the first class of differentiability for the topological equivalence.
, which, as mentioned in remark 3.6, was used by the authors in [Reference Dragičević, Zhang and Zhang11] in order to prove the first class of differentiability for the topological equivalence.
Remark 4.8 Similarly as we commented on remark 3.5, given any linear system (2.1) with nonuniform exponential dichotomy, a wide family of perturbations $f$![]() can be found such that $M\nu \,{\rm e}^{-\varepsilon }<1$
can be found such that $M\nu \,{\rm e}^{-\varepsilon }<1$![]() , $a(M+\nu )<{\rm e}^\varepsilon$
, $a(M+\nu )<{\rm e}^\varepsilon$![]() and $aM^2\,{\rm e}^{-\lambda }<1$
and $aM^2\,{\rm e}^{-\lambda }<1$![]() , since all of these inequalities can be achieved by setting $f$
, since all of these inequalities can be achieved by setting $f$![]() small enough and with a fast enough decreasing rate.
small enough and with a fast enough decreasing rate.
On the other hand, by theorem 4.3, it would be enough to verify (d7) in order to achieve $C^2$![]() -topological equivalence. Nevertheless, as explained in remark 3.13, this cannot be proved with the tools developed in this study.
-topological equivalence. Nevertheless, as explained in remark 3.13, this cannot be proved with the tools developed in this study.
5. Conjectures for high-order derivatives
In this section we seek conditions that generalize our previous hypothesis in order to obtain higher-order derivatives for the homeomorphism. To begin we introduce a new condition to replace (d5):
(d5′) For every fixed $k\in \mathbb {Z}^+$
 , $u\mapsto f(k,u)$
, $u\mapsto f(k,u)$ is a $C^r$
is a $C^r$ map and there are functions $\Gamma _s:\mathbb {Z}^+\to \mathbb {R}^+$
map and there are functions $\Gamma _s:\mathbb {Z}^+\to \mathbb {R}^+$ , $0\leq s \leq r$
, $0\leq s \leq r$ , $m \in \mathbb {Z}^+$
, $m \in \mathbb {Z}^+$ such that:
\[ \left\Vert{\frac{\partial^s f}{\partial u^s}(j,u)}\right\Vert \leq \Gamma_s(j),\quad \text{for every }j\in \mathbb{Z}^+. \]
such that:
\[ \left\Vert{\frac{\partial^s f}{\partial u^s}(j,u)}\right\Vert \leq \Gamma_s(j),\quad \text{for every }j\in \mathbb{Z}^+. \]
Conjecture 5.1 Suppose that conditions (d1), (d4) and (d5$'$![]() ) are verified. Then, there are functions $\pi _{s,m}:\mathbb {Z}^+\to \mathbb {R}^+$
) are verified. Then, there are functions $\pi _{s,m}:\mathbb {Z}^+\to \mathbb {R}^+$![]() , for every $1\leq s \leq r$
, for every $1\leq s \leq r$![]() and $m \in \mathbb {Z}^+$
and $m \in \mathbb {Z}^+$![]() such that
such that
Moreover, the family of functions $\{\pi _{s,m}: 1\leq s\leq r,\ m\in \mathbb {Z}^+\}$![]() can be recursively found, i.e. each $\pi _{s,m}$
can be recursively found, i.e. each $\pi _{s,m}$![]() can be written as a function of those $\Gamma _{t}$
can be written as a function of those $\Gamma _{t}$![]() and $\pi _{t,m}$
and $\pi _{t,m}$![]() with $t\leq s$
with $t\leq s$![]() .
.
Note that conjecture 5.1 is true for $r=1$![]() and $r=2$
and $r=2$![]() , since in the proof of lemma 3.1 we showed that $\pi _{1,m}=\mathcal {A}_m$
, since in the proof of lemma 3.1 we showed that $\pi _{1,m}=\mathcal {A}_m$![]() verifies (5.1) for $s=1$
verifies (5.1) for $s=1$![]() and in lemma 4.4 we proved that
and in lemma 4.4 we proved that

satisfies (5.1) for $s=2$![]() . Moreover, the identity
. Moreover, the identity

shows the recursive relation we established. With these new notations, let us consider the following conditions:
(d2′) For each fixed $m\in \mathbb {Z}^+$
 , we have
\[ \sum_{j=m}^{\infty}\Vert{\mathcal{G}(0,j+1)}\Vert \Gamma_0(j)<{+}\infty. \]
, we have
\[ \sum_{j=m}^{\infty}\Vert{\mathcal{G}(0,j+1)}\Vert \Gamma_0(j)<{+}\infty. \]
(d6′) For each fixed $m\in \mathbb {Z}^+$
 , we have
\[ \sum_{j=m}^{\infty}\Vert{\mathcal{G}(0,j+1)}\Vert \Gamma_1(j)\pi_{1,m}(j)<{+}\infty. \]
, we have
\[ \sum_{j=m}^{\infty}\Vert{\mathcal{G}(0,j+1)}\Vert \Gamma_1(j)\pi_{1,m}(j)<{+}\infty. \]
(d8) For each fixed $m\in \mathbb {Z}^+$
 , we have
\[ \sum_{j=m}^{\infty} \Vert{\mathcal{G}(0,j+1)}\Vert \left\{\pi_{2,m}(j)\Gamma_1(j)+\Gamma_2(j)\pi_{1,m}(j)\right\}<{+}\infty. \]
, we have
\[ \sum_{j=m}^{\infty} \Vert{\mathcal{G}(0,j+1)}\Vert \left\{\pi_{2,m}(j)\Gamma_1(j)+\Gamma_2(j)\pi_{1,m}(j)\right\}<{+}\infty. \]
A short calculus shows that (d2$'$![]() ) is equivalent to (d2). It is immediate that (d6) is a more exigent condition than (d6$'$
) is equivalent to (d2). It is immediate that (d6) is a more exigent condition than (d6$'$![]() ), while (d6$'$
), while (d6$'$![]() ) does not imply (d6) in general, but it is easy to see that if we replace (d6) with (d6$'$
) does not imply (d6) in general, but it is easy to see that if we replace (d6) with (d6$'$![]() ) in all of our previous results, all conclusions follow in the same fashion. Similarly, (d8) replaces condition (4.3) from lemma 4.1.
) in all of our previous results, all conclusions follow in the same fashion. Similarly, (d8) replaces condition (4.3) from lemma 4.1.
The following construction shows the utility of this conjecture. Suppose conjecture 5.1 is true. Choose a fixed $m \in \mathbb {Z}^+$![]() and consider the set of functions:
and consider the set of functions:

Consider the module $\mathbb {Z}[\mathfrak {S}_m],$![]() that is, all $\mathbb {Z}$
that is, all $\mathbb {Z}$![]() -linear combinations of the functions in $\mathfrak {S}_m$
-linear combinations of the functions in $\mathfrak {S}_m$![]() , and define the $\mathbb {Z}$
, and define the $\mathbb {Z}$![]() -linear map $\mathbb {D}_m:\mathbb {Z}[\mathfrak {S}_m]\to \mathbb {Z}[\mathfrak {S}_m]$
-linear map $\mathbb {D}_m:\mathbb {Z}[\mathfrak {S}_m]\to \mathbb {Z}[\mathfrak {S}_m]$![]() given by
given by
• $\mathbb {D}_m(\Gamma _s)=\Gamma _{s+1}\pi _{1,m}$
 , for every $0\leq s < r-1$
, for every $0\leq s < r-1$ and $\mathbb {D}_m(\Gamma _r)=0$
and $\mathbb {D}_m(\Gamma _r)=0$ .
.• $\mathbb {D}_m(\pi _{s,m})=\pi _{s+1,m}$
 , for every $1\leq s < r-1$
, for every $1\leq s < r-1$ and $\mathbb {D}_m(\pi _{r,m})=0$
and $\mathbb {D}_m(\pi _{r,m})=0$ .
.• $\mathbb {D}_m(fg)=\mathbb {D}_m(f)g+f\mathbb {D}_m(g)$
 , for every $f,g \in \mathbb {Z}[\mathfrak {S}_m]$
, for every $f,g \in \mathbb {Z}[\mathfrak {S}_m]$ such that $fg\in \mathbb {Z}[\mathfrak {S}_m]$
such that $fg\in \mathbb {Z}[\mathfrak {S}_m]$ .
.
Now we can introduce our final condition:
(d9) For each fixed $m\in \mathbb {Z}^+$
 and every $0\leq s\leq r$
and every $0\leq s\leq r$ , we have
\[ \sum_{j=m}^{\infty}\Vert{\mathcal{G}(0,j+1)}\Vert \mathbb{D}^s_m(\Gamma_0)(j)<{+}\infty. \]
, we have
\[ \sum_{j=m}^{\infty}\Vert{\mathcal{G}(0,j+1)}\Vert \mathbb{D}^s_m(\Gamma_0)(j)<{+}\infty. \]
It is easy to see (d9) corresponds to (d2$'$![]() ) if $r=0$
) if $r=0$![]() , to (d2$'$
, to (d2$'$![]() ) and (d6$'$
) and (d6$'$![]() ) if $r=1$
) if $r=1$![]() and to (d2$'$
and to (d2$'$![]() ), (d6$'$
), (d6$'$![]() ) and (d8) if $r=2$
) and (d8) if $r=2$![]() . Thus, we can rewrite some of our previous results as follows:
. Thus, we can rewrite some of our previous results as follows:
• Corollary 3.3. If conditions (d1), (d3), (d4), (d5$'$
 ) and (d9) with $r=1$
) and (d9) with $r=1$ are verified, then $\eta \mapsto G(k,\eta )$
are verified, then $\eta \mapsto G(k,\eta )$ is a $C^1$
is a $C^1$ map and $\xi \mapsto H(k,\xi )$
map and $\xi \mapsto H(k,\xi )$ is almost everywhere differentiable for every fixed $k\in \mathbb {Z}^+$
is almost everywhere differentiable for every fixed $k\in \mathbb {Z}^+$ .
.• Theorem 3.12. If conditions (d1), (d3), (d4), (d5$'$
 ) and (d9) with $r=1$
) and (d9) with $r=1$ , and (d7) are verified, then systems (2.1) and (2.2) are $C^1$
, and (d7) are verified, then systems (2.1) and (2.2) are $C^1$ -topologically equivalent on $\mathbb {Z}^+$
-topologically equivalent on $\mathbb {Z}^+$ .
.• Corollary 4.2. If conditions (d1), (d3), (d4), (d5$'$
 ) and (d9) with $r=2$
) and (d9) with $r=2$ are verified, then $\eta \mapsto G(k,\eta )$
are verified, then $\eta \mapsto G(k,\eta )$ is a $C^2$
is a $C^2$ map and $\xi \mapsto H(k,\xi )$
map and $\xi \mapsto H(k,\xi )$ is almost everywhere two times differentiable for every fixed $k\in \mathbb {Z}^+$
is almost everywhere two times differentiable for every fixed $k\in \mathbb {Z}^+$ .
.• Theorem 4.3. If conditions (d1), (d3), (d4), (d5$'$
 ) and (d9) with $r=2$
) and (d9) with $r=2$ , and (d7) are verified, then systems (2.1) and (2.2) are $C^2$
, and (d7) are verified, then systems (2.1) and (2.2) are $C^2$ -topologically equivalent on $\mathbb {Z}^+$
-topologically equivalent on $\mathbb {Z}^+$ .
.
Naturally, this raises the following conjectures:
Conjecture 5.2 Suppose conjecture 5.1 is true for some $r\in \mathbb {N}$![]() , $r\geq 3$
, $r\geq 3$![]() . If conditions (d1), (d3), (d4), (d5$'$
. If conditions (d1), (d3), (d4), (d5$'$![]() ) and (d9) are verified, then systems (2.1) and (2.2) are topologically equivalent on $\mathbb {Z}^+$
) and (d9) are verified, then systems (2.1) and (2.2) are topologically equivalent on $\mathbb {Z}^+$![]() with maps $H$
with maps $H$![]() and $G$
and $G$![]() such that for every fixed $k\in \mathbb {Z}^+$
such that for every fixed $k\in \mathbb {Z}^+$![]() $\eta \mapsto G(k,\eta )$
$\eta \mapsto G(k,\eta )$![]() is a $C^r$
is a $C^r$![]() map and $\xi \mapsto H(k,\xi )$
map and $\xi \mapsto H(k,\xi )$![]() is almost everywhere $r$
is almost everywhere $r$![]() times differentiable.
times differentiable.
Conjecture 5.3 Suppose conjecture 5.1 is true for some $r\in \mathbb {N}$![]() , $r\geq 3$
, $r\geq 3$![]() . If conditions (d1), (d3), (d4), (d5$'$
. If conditions (d1), (d3), (d4), (d5$'$![]() ), (d7) and (d9) are verified, then systems (2.1) and (2.2) are $C^r$
), (d7) and (d9) are verified, then systems (2.1) and (2.2) are $C^r$![]() -topologically equivalent on $\mathbb {Z}^+$
-topologically equivalent on $\mathbb {Z}^+$![]() .
.
Remark 5.4 Notice that in (5.1) the bounds for each partial derivative of order $1\leq s \leq r$![]() are uniform in $\eta$
are uniform in $\eta$![]() for each $j \geq m$
for each $j \geq m$![]() where $m$
where $m$![]() is the initial time of the solution of (2.2). Thus, these conjectures are interesting in the sense that is not enough that the partial derivatives exist in order to conclude that the homeomorphisms to have some class of differentiability (actually they always exists if (d5$'$
is the initial time of the solution of (2.2). Thus, these conjectures are interesting in the sense that is not enough that the partial derivatives exist in order to conclude that the homeomorphisms to have some class of differentiability (actually they always exists if (d5$'$![]() ) is granted), rather the uniform boundedness of these derivatives is what plays an important role concerning the regularity of such homeomorphisms, and this is what was showed in the proof of the cases $r=1,2.$
) is granted), rather the uniform boundedness of these derivatives is what plays an important role concerning the regularity of such homeomorphisms, and this is what was showed in the proof of the cases $r=1,2.$![]()
Acknowledgments
We are very grateful to an anonymous referee. We deeply appreciate the constructive criticism, kind suggestions and careful insight which assisted us to obtain a better understanding and writing of these results.
Financial support
This research has been partially supported by ANID, Beca Nacional de Magister 22200774 and FONDECYT Regular 1200653.