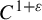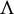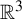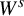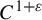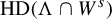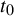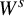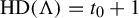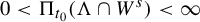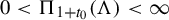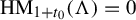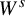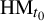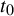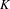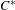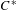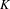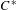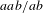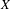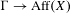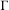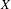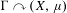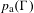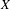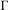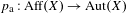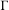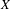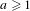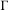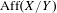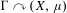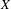We extend the results of Hasselblatt and Schmeling [Dimension product structure of hyperbolic sets. Modern Dynamical Systems and Applications. Eds. B. Hasselblatt, M. Brin and Y. Pesin. Cambridge University Press, New York, 2004, pp. 331–345] and of Rams and Simon [Hausdorff and packing measure for solenoids. Ergod. Th. & Dynam. Sys. 23 (2003), 273–292] for
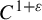 $C^{1+\varepsilon }$
hyperbolic, (partially) linear solenoids
$C^{1+\varepsilon }$
hyperbolic, (partially) linear solenoids
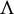 $\Lambda $
over the circle embedded in
$\Lambda $
over the circle embedded in
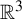 $\mathbb {R}^3$
non-conformally attracting in the stable discs
$\mathbb {R}^3$
non-conformally attracting in the stable discs
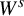 $W^s$
direction, to nonlinear solenoids. Under the assumptions of transversality and on the Lyapunov exponents for an appropriate Gibbs measure imposing thinness, as well as the assumption that there is an invariant
$W^s$
direction, to nonlinear solenoids. Under the assumptions of transversality and on the Lyapunov exponents for an appropriate Gibbs measure imposing thinness, as well as the assumption that there is an invariant
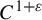 $C^{1+\varepsilon }$
strong stable foliation, we prove that Hausdorff dimension
$C^{1+\varepsilon }$
strong stable foliation, we prove that Hausdorff dimension
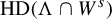 $\operatorname {\mathrm {HD}}(\Lambda \cap W^s)$
is the same quantity
$\operatorname {\mathrm {HD}}(\Lambda \cap W^s)$
is the same quantity
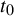 $t_0$
for all
$t_0$
for all
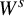 $W^s$
and else
$W^s$
and else
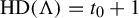 $\mathrm {HD}(\Lambda )=t_0+1$
. We prove also that for the packing measure,
$\mathrm {HD}(\Lambda )=t_0+1$
. We prove also that for the packing measure,
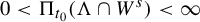 $0<\Pi _{t_0}(\Lambda \cap W^s)<\infty $
, but for Hausdorff measure,
$0<\Pi _{t_0}(\Lambda \cap W^s)<\infty $
, but for Hausdorff measure,
 $\mathrm {HM}_{t_0}(\Lambda \cap W^s)=0$
for all
$\mathrm {HM}_{t_0}(\Lambda \cap W^s)=0$
for all
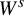 $W^s$
. Also
$W^s$
. Also
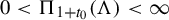 $0<\Pi _{1+t_0}(\Lambda ) <\infty $
and
$0<\Pi _{1+t_0}(\Lambda ) <\infty $
and
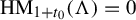 $\mathrm {HM}_{1+t_0}(\Lambda )=0$
. A technical part says that the holonomy along unstable foliation is locally Lipschitz, except for a set of unstable leaves whose intersection with every
$\mathrm {HM}_{1+t_0}(\Lambda )=0$
. A technical part says that the holonomy along unstable foliation is locally Lipschitz, except for a set of unstable leaves whose intersection with every
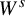 $W^s$
has measure
$W^s$
has measure
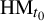 $\mathrm {HM}_{t_0}$
equal to 0 and even Hausdorff dimension less than
$\mathrm {HM}_{t_0}$
equal to 0 and even Hausdorff dimension less than
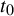 $t_0$
. The latter holds due to a large deviations phenomenon.
$t_0$
. The latter holds due to a large deviations phenomenon.
 $K$-theory
$K$-theory