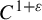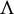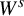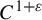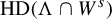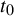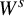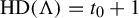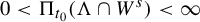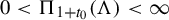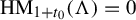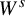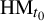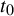Hausdorff and packing dimensions and measures for nonlinear transversally non-conformal thin solenoids

Abstract

We extend the results of Hasselblatt and Schmeling [Dimension product structure of hyperbolic sets. Modern Dynamical Systems and Applications. Eds. B. Hasselblatt, M. Brin and Y. Pesin. Cambridge University Press, New York, 2004, pp. 331–345] and of Rams and Simon [Hausdorff and packing measure for solenoids. Ergod. Th. & Dynam. Sys. 23 (2003), 273–292] for $C^{1+\varepsilon }$ hyperbolic, (partially) linear solenoids $\Lambda $ over the circle embedded in $\mathbb {R}^3$ non-conformally attracting in the stable discs $W^s$ direction, to nonlinear solenoids. Under the assumptions of transversality and on the Lyapunov exponents for an appropriate Gibbs measure imposing thinness, as well as the assumption that there is an invariant $C^{1+\varepsilon }$ strong stable foliation, we prove that Hausdorff dimension $\operatorname {\mathrm {HD}}(\Lambda \cap W^s)$ is the same quantity $t_0$ for all $W^s$ and else $\mathrm {HD}(\Lambda )=t_0+1$ . We prove also that for the packing measure, $0<\Pi _{t_0}(\Lambda \cap W^s)<\infty $ , but for Hausdorff measure, $\mathrm {HM}_{t_0}(\Lambda \cap W^s)=0$ for all $W^s$ . Also $0<\Pi _{1+t_0}(\Lambda ) <\infty $ and $\mathrm {HM}_{1+t_0}(\Lambda )=0$ . A technical part says that the holonomy along unstable foliation is locally Lipschitz, except for a set of unstable leaves whose intersection with every $W^s$ has measure $\mathrm {HM}_{t_0}$ equal to 0 and even Hausdorff dimension less than $t_0$ . The latter holds due to a large deviations phenomenon.

1 Introduction. Statement of main results

We consider the solid torus

$$ \begin{align*}M=S^1 \times \mathbb{D},\quad \mathbb{D}=\{(y,z)\in\mathbb{R}^2:y^2+z^2<1\}, \end{align*} $$

where $S^1=\mathbb {R}/2\pi \mathbb {Z}$ .

Consider a mapping $f:M\to M$ of class $C^{1+\varepsilon }$ , that is, with its differential being Hölder continuous, given by the formula

(1.1) $$ \begin{align} f(x,y,z)=(\eta(x), \unicode{x3bb}( x,y )+ u(x), \nu( x,y,z ) + v(x) ), \end{align} $$

with $\unicode{x3bb} (x,0)=\nu (x,0,0)=0$ . Assume that f has period $2\pi $ with respect to x so that it is well-defined on M. Assume that $\eta $ has degree $d>1$ .

Denote $\eta '={d\eta }/{dx}, \; \unicode{x3bb} '={d\unicode{x3bb} }/{dy}, \; \nu '={d\nu }/{dz}$ . Assume that $0<\nu ' < \unicode{x3bb} '<1$ and $1<\eta '<1/\unicode{x3bb} ' $ (some of these inequalities will be weakened later on to inequalities between Lyapunov exponents on $\Lambda $ , that is, integrals with respect to certain Gibbs measure). We could allow here $-1<\unicode{x3bb} '<0$ (the same for $\nu '$ ), but we assume it is positive to simplify the notation. We assume also that $f:M\to M$ is injective (using sometimes the name embedded).

Such a solenoid in the linear case (or at least if $\eta '\equiv d$ ) can be called a uniformly thin solenoid (for the definition of a thick linear solenoid, where $\eta '\unicode{x3bb} '>1$ , see e.g. [15]). Compare the stronger uniform dissipation condition in §1.4.

Then

$$ \begin{align*}\Lambda:=\bigcap_{n=0}^\infty f^n(M) \end{align*} $$

is an invariant hyperbolic set, so called an expanding attractor. The assumption f is injective on M can be weakened to the assumption f is injective on $\Lambda $ , by replacing M with a solid torus being a sufficiently thin neighbourhood of $\Lambda $ . However, for clarity, we assume the injectivity of f directly on M.

For each $p=(x,y,z)\in \Lambda $ , the disc $W^s_x=W^s(p)=\{(x',y',z'):x'=x\}$ is a (principal) component (in M) of the stable manifold of p and the interval $W^{ss}_{x,y}=W^{ss}(p)=\{(x',y',z'):x'=x, y'=y\}$ is a (principal) component of strong stable manifold of p. Unstable manifolds $W^u(p)$ are more complicated, each is dense in $\Lambda $ and for each $x,x'\in \mathbb {R}^1$ , the unstable lamination of $\Lambda $ defines the holonomy map $h_{x,x'}:W^s_{x/2\pi \mathbb {Z}}\cap \Lambda \to W^s_{x'/2\pi \mathbb {Z}}\cap \Lambda $ .

Sometimes we write $W^s_x$ in place of $W^s_{x/2\pi \mathbb {Z}}$ . Denote by $\pi _x$ the projection $(x,y,z)\mapsto x$ . The part of global $W^u(p)$ , which is the lift of $[x,x']\subset \mathbb {R}$ for $\pi _x$ , will be denoted $W^u_{[x,x']}(p)$ . For $[x,x']$ equal to $[0,2\pi ]$ or slightly bigger, clear from the context, we shall sometimes just write $W^u(p)$ .

Denote by $\pi _{x,y}$ the projection $(x,y,z) \mapsto (x,y)$ . We assume in this paper the following transversality assumption: each intersection of two distinct $\pi _{x,y}(W^u(p))$ and $\pi _{x,y}(W^u(q))$ is transversal.

Let $\mu =\mu _{t_0}$ be the Gibbs measure (equilibrium state) on $\Lambda $ for the potential $t_0\log |\unicode{x3bb} '|$ , where $t=t_0$ is zero of the topological pressure $t\mapsto P(f,t\log \unicode{x3bb} ')$ . The measure $\mu $ can be called geometric or SRB in the stable direction or just stable SRB-measure. Denote by $\mu ^s_x$ its conditional measures on $W^s_x$ for each x, see explanations following Lemma 3.6.

Definition 1.1. (Thin solenoid)

The solenoid $\Lambda $ for injective $f:M\to M$ as in equation (1.1) satisfying $\chi _{\mu }(\nu ')<\chi _{\mu } (\unicode{x3bb} ')< -\chi _{\mu }(\eta ')$ for $\mu $ being the stable SRB-measure on $\Lambda $ , for Lyapunov exponents $\chi _{\mu }(\xi ):=\int \log \xi \, d\mu $ for $\xi =\nu ',\unicode{x3bb} '$ and $\eta '$ , respectively, is called a non-uniformly thin, or just thin, solenoid.

We prove the following theorems.

Theorem 1.2. Let $\Lambda $ be a non-uniformly thin solenoid for $f:M\to M$ as in the definition above, which satisfies the transversality assumption. Then, for $\operatorname {\mathrm {HD}}$ denoting Hausdorff dimension and for every $x\in S^1$ :

1. (1) $\operatorname {\mathrm {HD}}(\Lambda \cap W^s_x)=t_0$ ;

2. (2) $\operatorname {\mathrm {HD}}(\Lambda )=1+t_0$ .

Theorem 1.3. Under the assumptions of Theorem 1.2, for $\Pi _t$ denoting packing measure in dimension t, for every $x\in S^1$ , it holds $0<\Pi _{t_0}(\Lambda \cap W^s_x)<\infty $ . Moreover, $ 0<\Pi _{1+t_0}(\Lambda )<\infty $ .

Theorem 1.4. Under the assumptions of Theorem 1.2, for $\mathrm {HM}_t$ denoting Hausdorff measure in dimension t, $\mathrm {HM}_{t_0}(\Lambda \cap W^s_x)=0$ for every $x\in S^1$ . Moreover, $\mathrm {HM}_{1+t_0}(\Lambda ) =0$ .

Now we need the following definition.

Definition 1.5. (Bunching condition)

We say that our thin solenoid $\Lambda $ satisfies the bunching condition if $\eta '(x)> \unicode{x3bb} '(x)/\nu '(x)$ for every $x\in \Lambda $ .

A theorem used in particular to compare sizes of $\Lambda \cap W^s_x$ for varying x, is the following.

Theorem 1.6. Under the assumptions of Theorem 1.2, if the bunching condition is satisfied, then all the holonomies $h_{x,x'}$ for $x,x'\in \mathbb {R}$ are uniformly Lipschitz continuous.

If the bunching condition is not assumed, then for each R, there exists $\operatorname {\mathrm {Lip}}(R)>0$ such that for each x, there is a set $L_x\subset W^s_x\cap \Lambda $ such that for all $x'$ satisfying $|x-x'|<R$ , the holonomies $h_{x,x'}$ are locally bi-Lipschitz continuous with a common constant $\operatorname {\mathrm {Lip}}(R)$ and $\mu ^s_x(\Lambda \cap W^s_x \setminus L_x)= 0$ .

In fact, $\mu ^s_x(NL^w \cap W^s_x)=0$ for a certain weak non-Lipschitz set $NL^w$ invariant under all $h_{x,x'}$ for $0\le x,x'\le 2\pi $ , which, intersected with $W_x^s$ , is bigger than the complement of Lipschitz $L_x$ . Moreover, $\operatorname {\mathrm {HD}} (NL^w \cap W^s_x) < t_0$ .

Here ‘local’ means for every $p\in L_x$ , there exists $\delta $ such that for all $q\in W^s_x\cap \Lambda \cap B(p,\delta )$ and $|x'-x|<R$ , the Lipschitz condition with the constant $\operatorname {\mathrm {Lip}}(R)$ holds for $h_{x,x'}$ .

The bunching condition above appeared in a related setting in [13], see also [6, Theorem 4.21] for a stronger conclusion that the unstable foliation is $C^1$ .

Some of the assertions above hold also for the projections to the $\{(x,y)\}$ plane, in particular the following.

Theorem 1.7. Under the assumptions of Theorem 1.2, $\operatorname {\mathrm {HD}}(\pi _{x,y}(\Lambda \cap W^s_x))=t_0$ and $\operatorname {\mathrm {HD}}(\pi _{x,y}(\Lambda ))=1+t_0$ .

We do not know if $0<\Pi _{t_0}(\pi _{x,y}(\Lambda \cap W^s_x))<\infty $ or $ 0<\Pi _{1+t_0}(\pi _{x,y}(\Lambda ))<\infty $ .

The assertions of Theorem 1.2 almost automatically hold for Hausdorff dimension replaced by the upper box dimension $\overline {\operatorname {\mathrm {BD}}}$ . Indeed, the estimates from below follow from $\operatorname {\mathrm {HD}}\le \overline {\operatorname {\mathrm {BD}}}$ . The estimate $\overline {\operatorname {\mathrm {BD}}}(\Lambda \cap W^s_x)\le t_0$ follows from Lemma 4.3. The estimate $\overline {\operatorname {\mathrm {BD}}}(\Lambda )\le 1+ t_0$ follows from the proof of Theorem 4.2, Step 3.

1.1 On the linear case

The mapping f in equation (1.1) is called lower triangular (because such is the differential $Df$ in the $y,z$ direction) nonlinear. Our paper complements the study of the linear diagonal case

(1.2) $$ \begin{align} f(x,y,z)=(dx(\mathrm{mod}\ 2\pi), \unicode{x3bb} y + u(x), \nu z + v(x) ), \end{align} $$

with $0<\nu <\unicode{x3bb} < 1/d$ . It was done by Hasselblatt and Schmeling in [9], where, nevertheless, there were hints concerning the nonlinear situations, and by Rams and Simon [17]. Namely, Theorems 1.2,1.3, and 1.4 generalize [9] and Theorem 1.4 generalizes [17]. It should be noted that Theorem 1.3 was proved in [17] only for Lebesgue almost every (a.e.) x.

1.2 Transversally conformal case

This is the case where f is conformal on every $W^s$ well understood. Theorems 1.2 and 1.3 hold, though the dimension $t_0$ can be larger than one (in a thick case). Packing and Hausdorff measures on $W^s$ in dimension $t_0$ are equivalent. In fact, this is a transversally complex one-dimensional (1D) situation, whereas our non-conformal case corresponds after $\pi _{x,y}$ -projection to a transversally real 1D situation with overlaps.

1.3 Motivation

Let us present a geometric picture of the solenoid. It helps to think not of the solenoid itself (which is locally just a Cantor bouquet of almost parallel lines and is hard to analyse with an untrained eye) but of its approximations $f^n(M)$ . Each of the approximations is a tube, winding around along $S^1$ and going around $d^n$ times. Thus, every section of $f^n(M)$ with a disc $W_x^s=\{x\}\times \mathbb D$ is a disjoint union of $d^n$ components, where each disc is a (slightly deformed) ellipse with exponentially increasing ratio of the large semiaxis to the small semiaxis, and all the large semiaxes pointing roughly in the same $\{y\}$ direction. See Figure 1. As already mentioned, the approximate ellipses are disjoint, but there are plenty of sections in which some of the ellipses are very close to each other, in a distance exponentially smaller than their diameters. One of the main concerns in our study will be the understanding of the way those ellipses ‘move’ as we move the section plane around $S^1$ .

Figure 1 Geometric picture of the solenoid.

This picture closely resembles the picture of an affine iterated function system, or maybe even better: the averaged picture of many different but similar affine iterated function systems (as each ellipse in the section comes with a different backward path, and is thus produced by a different collection of non-conformal contracting maps). An important element of the picture is that the contracting maps in the sections satisfy a version of the domination property, that is, the strong contracting direction in one iteration stays close to the strong contracting direction in the following iterations. That is, we clearly have two different negative Lyapunov exponents in our system.

This picture lets us expect a behaviour similar to the known generic behaviour of affine iterated function systems. We expect the Hausdorff and packing and box dimensions of each section to be given by Falconer’s singular value pressure formula, which, in our ‘thin’ case, should depend only on what happens in the expanding and weakly contracting directions (in particular, the dimensions should be preserved by the projection to the $\{(x,y)\}$ plane). Moreover, like in simpler solenoid cases, we expect that the situations when two ellipses pass nearby (which are unavoidable owing to the very geometry of the solenoid) should have an effect strong enough to zero the Hausdorff measure, but the packing measure should stay positive and finite. Those are exactly the statements we eventually prove in Theorems 1.2–1.4 and 1.7.

Hasselblatt and Schmeling stated in [9] (see some history and other references there, in particular [3]) the following.

Conjecture 1.8. The fractal dimension of a hyperbolic set is the sum of those of its stable and unstable slices, where ‘fractal’ can mean either Hausdorff or upper box dimension.

For solenoids, in [9] and here, an affirmative answer on Hausdorff dimension has been proven. Hausdorff dimension in the stable direction is $t_0$ and in unstable 1, that is, $1+t_0$ together. Notice that this is dimension $t_0$ of conditional measures of $\mu $ geometric (SRB) in the stable direction (see above) and of dimension 1 of an SRB measure in the unstable direction. Both SRB measures are usually different (even mutually singular), unless (e.g.) in the diagonal linear case, where both measures coincide with the measure of maximal entropy.

For any invariant hyperbolic measure $\nu $ , indeed $\operatorname {\mathrm {HD}}(\nu )=\operatorname {\mathrm {HD}}(\nu ^s)+\operatorname {\mathrm {HD}}(\nu ^u)$ , see [1], but even supremum of $\operatorname {\mathrm {HD}}(\nu )$ over invariant $\nu $ on $\Lambda $ can be less than $\operatorname {\mathrm {HD}}(\Lambda )$ . See e.g. [16]. So in a general case, one is forced to use both the SRB measures.

Finally note that Hasselblatt and Schmeling relax the assumption of transversality to the assumption that the intersections of $\pi _{x,y}$ projections of $W^u$ are non-flat. This in particular holds for all real analytic (that is, with the functions $u,v$ real analytic) linear solenoids, see [9]. A natural challenge would be to generalize our nonlinear theory to a general real-analytic (non-transversal) case.

1.4 Outline

In §3, we prove a part of Theorem 1.6 saying that the points in $W^s_x$ , where a holonomy $h_{x,x'}$ is not locally bi-Lipschitz, have measure $\mu $ equal 0. This follows (and clarifies) [9]. In fact, we prove that a bigger set has measure 0, the set of p which are not strong Lipschitz, called above weak non-Lipschitz. For such a p, the projection $\pi _{x,y}(W^u(p))$ intersects some $\pi _{x,y}(W^u(q))$ values for $q\notin W^u(p)$ arbitrarily close to $W^u(p)$ . Equivalently, p is strong Lipschitz if $W^{ss}_{\mathrm {loc}}(p)=\{p\}$ , so counting Hausdorff dimension only $E^s/E^{ss}$ counts, so $\operatorname {\mathrm {HD}}(\Lambda \cap W^s)=h_\mu (f)/-\chi _\mu (\unicode{x3bb} ') = t_0$ , where $h_\mu (f)$ is the measure (Kolmogorov’s) entropy, [10]. This is done in §4, and yields Theorem 1.2. Again we roughly follow [9].

In §3, Theorem 1.6 is in fact proved under the assumption stronger than $ \chi _\mu (\unicode{x3bb} ')< - \chi _\mu (\eta ') $ , namely under the assumption $\sup \unicode{x3bb} '<1/\sup \eta '$ , called uniform dissipation.

Note that Lipschitz property is related to Theorem 1.2 on Hausdorff dimension a little bit by chance, saying however that $\operatorname {\mathrm {HD}}(W^s_x\cap \Lambda )$ does not depend on x. In fact, holonomy being Lipschitz is a weak condition, e.g. it holds for all holonomies $h_{x,x'}$ provided $\eta '>\unicode{x3bb} '/\nu '$ , as in Theorem 1.6 (well known), as a twisting, hurting Lipschitz property cannot develop if $f^{-n}$ squeezes (by $(\eta ')^{-1}$ ) too much. The Lipschitz property is crucial to conclude $\operatorname {\mathrm {HD}}(W^s_x\cap \Lambda )=t_0 \Rightarrow \operatorname {\mathrm {HD}}(\Lambda )=1+t_0$ in Theorem 1.2. Compare Conjecture 1.8 above.

Theorem 1.3 is proved in §5. The proof has common points with [17]. Analysis is more delicate than in the proof of Theorem 1.2. We prove that for $\mu $ -a.e. p for a sequence of n values, the $\pi _{x,y}$ -projection of the tube $f^n(M)$ (truncated to $[0,2\pi ]$ ), called of order n containing p, intersects only a bounded number of other projections of tubes of order n.

Theorem 1.4 is proved in §6, again using an idea from [17]. It uses the fact of arbitrarily high multiplicity of overlapping of projections of tubes of order n for $\mu $ -a.e. p.

The estimate $\operatorname {\mathrm {HD}}(NL^w_x)<t_0$ in Theorem 1.6 is proved in §7, together with a more precise estimate, following from a large deviations estimate concerning Birkhoff averages.

Theorem 1.7 follows from other theorems because the assertions on dimensions are verified on the sets where the projection $\pi _{x,y}$ is finite-to-one.

Section 7 also contains a remark on general Williams 1D expanding attractors and a remark on a possibility of integrating general solenoids to triangular as in equation (1.1).

2 Holonomy along unstable lamination

Definition 2.1. We will now introduce a symbolic description on the attractor, defining an ‘almost bijection’ $\rho : \Sigma _d \to \Lambda $ , where $\Sigma _d = \{0,1,\ldots , d-1\}^{\mathbb {Z}}$ is the usual two-sided full-shift space on d symbols. Why it is only an ‘almost bijection’ will be explained soon. Moreover, it will be done in such a way that $\rho $ semi-conjugates the left shift $\varsigma $ acting on $\Sigma _d$ to $f|_\Lambda $ , namely $\rho \circ \varsigma = f \circ \rho $ . Denote else the elements of $\Sigma _d$ by $\underline {i}=(\ldots , i_{-n}, \ldots , i_0| i_1, \ldots , i_n, \ldots )$ , where the vertical line separates entries with non-positive indices from the entries with positive indices.

Let us start with closer explanations from the x coordinate. Looking at equation (1.1), we see that if $(x',y',z')=f(x,y,z)$ , then $x'$ does depend only on x, not on y or z. The restriction of f to the first coordinate is the d-to-1 expanding map $\eta $ . Denote by $a_0,\ldots ,a_{d-1},a_d=a_0$ the points of $\eta ^{-1}(0)\in \mathbb {R}/2\pi \mathbb {Z}=S^1$ numbered in increasing order. We can assume that $a_0=0=\eta (0)$ . For $i=0,1,\ldots , d-1$ , we denote $V_{|i}:=[a_i, a_{i+1}]\times \mathbb D$ ; those sets will be called vertical cylinders of level 1. We can then define for every $n=1,2, \ldots $ the vertical cylinders of level n, by

$$ \begin{align*}V_{i_1,\ldots,i_n}=\{p=(x,y,z)\in M:\ f^{k-1}(p)\in V_{|i_k} \text{ for}\ k=1,\ldots,n\}. \end{align*} $$

For every sequence $(i_1, i_2,\ldots )\in \{0,\ldots , d-1\}^{\mathbb {N}}$ , there exists exactly one $x\in S^1$ , such that

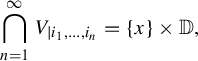(2.1) $$ \begin{align} \bigcap_{n=1}^\infty V_{|i_1,\ldots,i_n} = \{x\} \times \mathbb D, \end{align} $$

and vice versa: for all except countably many points $x\in S^1$ , there exists exactly one sequence $(i_1, i_2,\ldots )\in \{0,\ldots , d-1\}^{\mathbb {N}}$ such that equation (2.1) holds. The exceptions are the points x such that $\eta ^k(x)=0$ for some $k\in \mathbb {N}$ . For each of those points, one can find exactly two sequences satisfying equation (2.1). We note that $f^{k-1}(p)\in V_{|i_k}$ is equivalent to $\eta ^{k-1}(x)\in [a_{i_k},a_{i_k+1}]$ , so what we described up to this point is the usual construction of a symbolic description for an expanding map of the circle.

Let us now define the horizontal cylinders of level $n=0,1,2, \ldots $ by

$$\begin{align*}H_{i_{-n},\ldots, i_0|} := f^{n+1}(V_{|i_{-n},\ldots, i_0}), \end{align*}$$

and then define

$$\begin{align*}\rho(\underline{i}):= \lim_{n\to\infty} V_{|i_1,\ldots, i_n} \cap H_{i_{-n},\ldots, i_0|}. \end{align*}$$

The fact that $\rho $ semi-conjugates $\varsigma $ to $f|_\Lambda $ is clear from the definitions.

We will denote by $V(n)$ and $H(n)$ the sets of all vertical (respectively horizontal) cylinders of level n. For a given $p\in \Lambda $ , we will denote by $V_n(p)$ and $H_n(p)$ the vertical and horizontal cylinder of n, containing p. Sometimes we will just write $H_n$ and $V_n$ if we do not specify p.

We note that $\rho (\underline {i})=(x,y,z)$ , with x depending on $i_1, i_2, \ldots $ and $(y,z)$ depending on x and on $i_0,i_{-1},\ldots $ . It makes sense to write $\Sigma _d = \Sigma _d^- \times \Sigma _d^+$ with $\Sigma _d^-, \Sigma _d^+$ denoting the one-sided shift spaces on d symbols, the former given by non-positive entries and the latter by the positive entries. We then denote

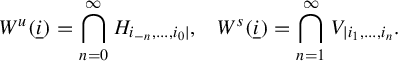$$\begin{align*}W^u(\underline{i}) = \bigcap_{n=0}^\infty H_{i_{-n},\ldots, i_0|},\ \ \ W^s(\underline{i}) = \bigcap_{n=1}^\infty V_{|i_1,\ldots, i_n}. \end{align*}$$

Clearly, $\rho (\underline {i}) = W^u(\underline {i}) \cap W^s(\underline {i})$ . We will also use the notation $W^u(p), W^s(p)$ for $p\in \Lambda $ , as the shortcut for $W^u(\rho ^{-1}(p)), W^s(\rho ^{-1}(p))$ . We note that as $\eta $ is expanding and $\unicode{x3bb} , \nu $ are contracting, $W^u(p)$ and $W^s(p)$ are pieces of the unstable and stable manifolds at $p\in \Lambda $ —which explains the notation used. This notation has been already introduced in §1, together with the notation $W^s_x$ for $x\in S^1$ .

Definition 2.2. Denote $\widehat f:= \pi _{x,y}\circ f \circ (\pi _{x,y})^{-1}$ , where $\pi _{x,y}$ is the projection $(x,y,z)\mapsto (x,y )$ , see §1. This definition makes sense, since f preserves the foliation $\{W^{ss}_x\}$ (vertical intervals here).

To simplify notation, we will sometimes denote objects being the projection of objects in M by $\pi _{x,y}$ by adding a hat over them, e.g. $\widehat \Lambda :=\pi _{x,y}(\Lambda )$ or $\widehat p =\pi _{x,y}(p)$ .

A reminder that the projection $(x,y,z)\mapsto x$ is denoted by $\pi _x$ , see §1. For any $p\in M$ , the point $\pi _x(p)$ will be sometimes denoted by $x(p)$ .

Denote $ \Gamma :=\{\widehat p \in \widehat \Lambda : \text { there exists } (\ldots ,i_0|)$ and $\text { there exists } (\ldots ,i^{\prime }_0|)$ with $i_0\not =i_0'$ , such that $\widehat W^u(\rho (\ldots ,i_0|))$ and $W^u(\rho (\ldots ,i_0'|))$ intersect at $\widehat p$ . Here $W^u=W^u_{[-L\eta _n^{-1}, 2\pi + L\eta _n^{-1}]}$ , where the ‘margins’ $L\eta _n^{-1}$ will be defined in Notation 2.4 and Definition 2.5.

In words, $\Gamma $ is a Cantor set, consisting of the intersections of the $\pi _{x,y}$ -projections of $W^u$ belonging to different (slightly extended) horizontal cylinders of level 0. It discounts intersections of the projections of $W^u$ being in the same cylinder of level 0. See Figure 2.

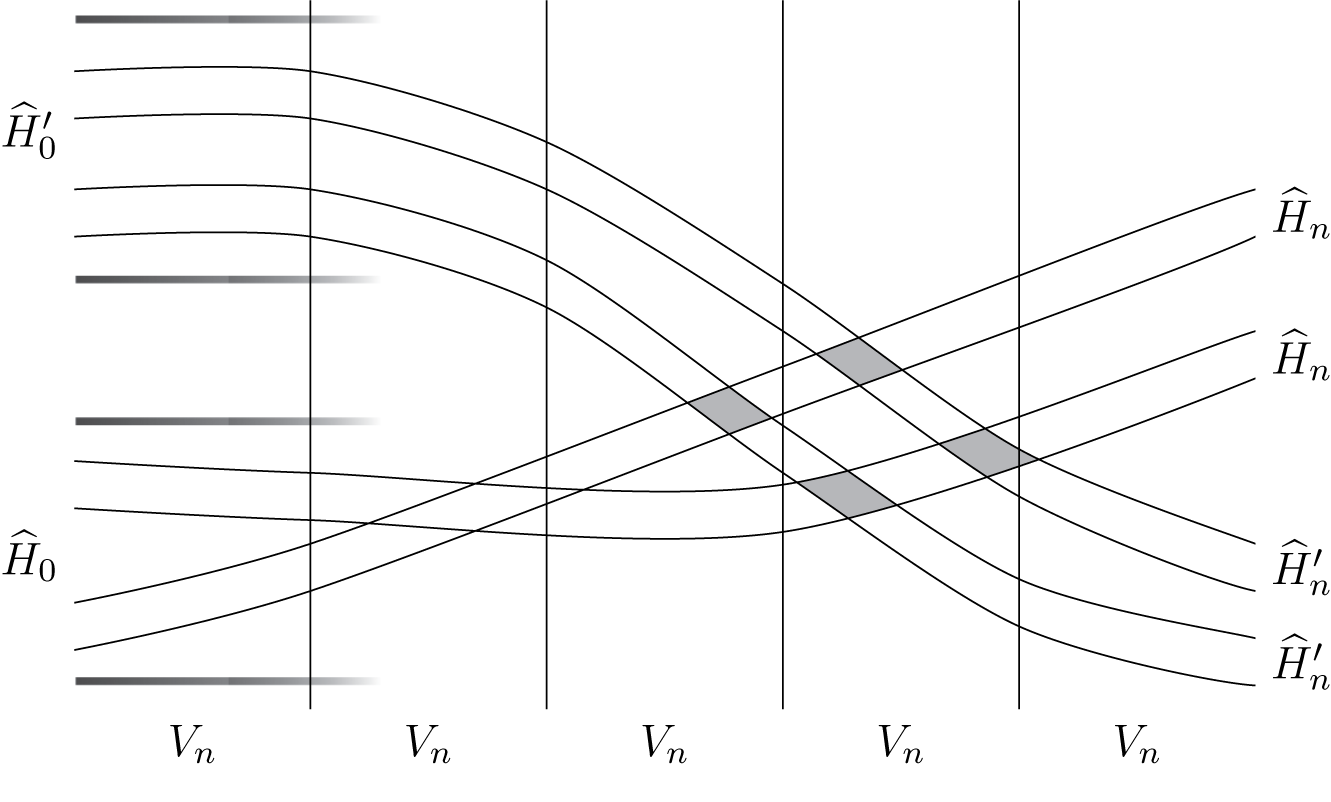
Figure 2 Projection to the $(x,y)$ -plane. Here, $H_n=H_{i_{-n},\ldots ,i_0 |}, H^{\prime }_n=H_{i^{\prime }_{-n},\ldots ,i^{\prime }_0 |}, V_n=V_{| i_1,\ldots ,i_n}$ .

2.1 (Unstable) transversality assumption

All intersections of these lines (that is, projections by $\pi _{x,y}$ of unstable manifolds) with different $i_0$ values are, in this paper, assumed to be mutually transversal.

Remark 2.3. Notice that by the compactness argument and the continuity of the sub-bundle $E^u_{\Lambda }$ , by the transversality assumption, all the intersection angles are bounded away from 0, say by $\alpha _0$ .

Also, by compactness and continuity of $E^u$ on $\Lambda $ , there exists $r_0>0$ such that if for $p,p' \in \Lambda \cap W^s$ , their mutual Euclidean distance is $r<r_0$ and their $i_0$ values are different, then the distance of their $\pi _{x,y}$ projections from $\Gamma $ , more precisely from the intersection $\widehat W^u(p)\cap \widehat W^u(p')$ , which is in particular non-empty, is bounded by $2r / \tan \alpha _0$ .

Remember that we consider f in the form of equation (1.1) and write $\eta ':={\partial \eta }/{\partial x}$ , $\unicode{x3bb} ':={\partial \unicode{x3bb} }/{\partial y}$ and $\nu ':={\partial \nu }/{\partial z}$ . Then we have the following.

Notation 2.4. We write $\xi _n^+(p)=\xi (p)\xi (f(p))\ldots \xi (f^n(p))$ for $\xi =\eta ', \unicode{x3bb} '$ or $\nu '$ . Write also $\xi _n^-(p):= \xi _n^+(f^{-n}(p))$ .

Definition 2.5. A point $p\in \Lambda $ is said to be strong locally Lipschitz if there is $L>0$ such that for all n big enough, denoting $(\eta _n^-(p)$ by $\eta _n$ ,

(2.2) $$ \begin{align} \operatorname{\mathrm{dist}}(\widehat{V_n(f^{-n}(p))}, \Gamma\cap \widehat{W}^u_{[-L\eta_n^{-1}, 2\pi + L\eta_n^{-1}]}(f^{-n}(p)) \ge L\eta_n^{-1}, \end{align} $$

with the distance in ${W}^u$ measured between the projections by $\pi _x$ in $\mathbb {R}$ .

Equivalently, we could replace here $\widehat {V_n(f^{-n}(p))}$ by $\widehat {f^{-n}(p)}$ . It would influence the constant L only.

By the unstable transversality and transversality of intersection of stable and unstable foliations, this is equivalent to the distance in the $\{(x,y)\}$ -plane satisfying

(2.3) $$ \begin{align} \operatorname{\mathrm{dist}}(\widehat{f^{-n}(p)}, \widehat{W}^u(p') \ge \operatorname{\mathrm{Const}} L \eta_n^{-1} \end{align} $$

for all $p'$ having $i_0$ different from the $i_0$ for $f^{-n}(p)$ .

We call all points p which are strong locally Lipschitz with the constant L such that equation (2.2) holds for all $q\in W^u(p)$ in place of p strong locally bi-Lipschitz.

Notice that this definition allows to say that the whole $W^u(p)$ is strong locally bi-Lipschitz and write

(2.4) $$ \begin{align} \operatorname{\mathrm{dist}}(\widehat{f^{-n}(W^u(p))}, \Gamma\cap \widehat{W}^u_{[-L\eta_n^{-1}, 2\pi + L\eta_n^{-1}]} (f^{-n}(p)) \ge L\eta_n^{-1}. \end{align} $$

Remark 2.6. Notice that if for $\widehat L>0$ strong locally Lipschitz condition, $\operatorname {\mathrm {dist}}(\widehat {f^{-n}(p)}, \Gamma \cap \widehat W^u(f^{-n}(p)))\ge \widehat L \eta _n (f^{-n}(p))^{-1}$ holds and $q\in W^u_{[0,2\pi ]}(p)$ , then $\operatorname {\mathrm {dist}}(\widehat {f^{-n}(q)}, \Gamma )\ge (\widehat L - \operatorname {\mathrm {Const}}) \eta _n (f^{-n}(q))^{-1}$ . So for equation (2.2) satisfied at p with $\widehat L> 2\operatorname {\mathrm {Const}}$ , the strong locally Lipschitz condition holds for all $q\in W^u(p) $ , with $L=\widehat L /2$ . So p is strong locally bi-Lipschitz.

Definition 2.7. For every $p\in \Lambda $ and $q\in W^u(p)\setminus \{p\}$ , one defines the holonomy map $h_{x(p),x(q)}: W^s(p)\to W^s(q)$ along unstable foliation (lamination) by $h_{x(p),x(q)}(v)$ being the only intersection point of $W^u(v)$ with $W^s(q)$ .

Theorem 2.8. For every $L_2>0$ , there exists $L_1>0$ such that for each p strong locally (bi)Lipschitz with the constant $L=L_1$ , there exists $n(p)$ such that for each $q\in W^u_{[0,2\pi ]} (p)$ , the holonomy between $W^s(p)\cap \Lambda $ and $W^s(q)\cap \Lambda $ , in $H_{n(p)}(p)\cap \Lambda $ , is locally bi-Lipschitz continuous at p with Lipschitz constant $L_2$ .

Here, at p means that for every $p'\in W^s(p)\cap H_{n(p)}(p)\cap \Lambda $ , we have

$$ \begin{align*}L_2^{-1}\operatorname{\mathrm{dist}} (p,p') \le \operatorname{\mathrm{dist}} (h_{\pi_x(p),\pi_x(q)}(p), h_{\pi_x(p),\pi_x(q)}(p') \le L_2 \operatorname{\mathrm{dist}} (p,p'), \end{align*} $$

where dist is the euclidean distance in $\mathbb {D}$ .

Proof We repeat (adjust) the calculations in [9]. Consider $q\kern1.2pt{\in}\kern1.2pt W^u(p)$ and ${p'\kern1.2pt{\in}\kern1.2pt W^s(p)\kern1.2pt{\cap}\kern1.2pt \Lambda }$ . Define $q':= h_{x(p),x(q)} (p')$ . Let $p'\in H_n(p)\setminus H_{n+1}(p)$ , that is, $p_{-n}=f^{-n}(p)$ and $p^{\prime }_{-n}=f^{-n}(p')$ are in different $H_0$ (Figure 3).

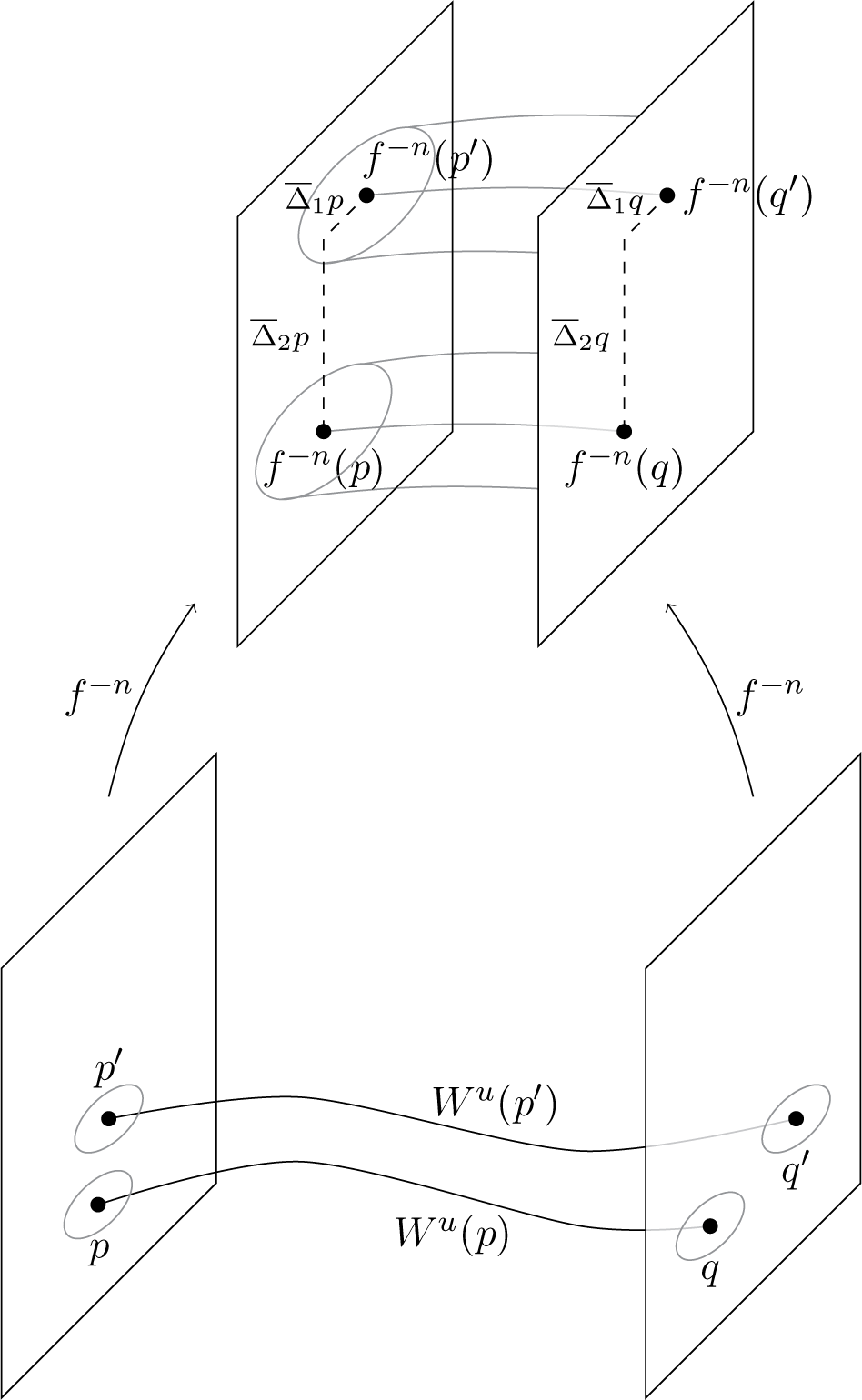
Figure 3 Holonomy twist.

Local Lipschitz continuity of the holonomy $h_{x(p),x(q)}$ at p would follow from the existence of a uniform upper bound of

(2.5) $$ \begin{align} \operatorname{\mathrm{dist}}(q,q') / \operatorname{\mathrm{dist}}(p,p') \end{align} $$

for $p'$ close enough to p, that is, n defined above, large.

It is comfortable to consider the distance $d=d_1 + d_2$ , the distances in the y and z coordinates.

We shall use the triangular form of the differential $ Df|_{\{y,z\}} = \Big [\begin {smallmatrix} \unicode{x3bb} ' & 0 \\ a & \nu ' \end {smallmatrix}\Big ]. $ Due to $\nu '<\unicode{x3bb} '$ , we have $Df^n|_{\{y,z\}}=\Big [\begin {smallmatrix} \unicode{x3bb} _n' & 0 \\ a_n & \nu _n' \end {smallmatrix}\Big ]$ , where $|a_n|\le \operatorname {\mathrm {Const}} \unicode{x3bb} _n$ . Write, according to the decomposition $d=d_1+d_2$ , $d(f^{-n}(p),f^{-n}(p')):=\overline \Delta p=\overline \Delta _1 p + \overline \Delta _2 p$ and $d(f^{-n}(q),f^{-n}(q')):=\overline \Delta q= \overline \Delta _1 q + \overline \Delta _2 q.$

We estimate

for a constant A depending on the angle between $W^u$ and $W^s$ . Here, $\overline{\unicode{x3bb}} _n, \overline {a_n}, \overline \nu _n$ are averages of derivatives $\unicode{x3bb} _n,a_n,\nu _n$ , respectively, on appropriate intervals, namely integrals divided by the lengths of the intervals, horizontal along y for two first integrals and vertical along z for the last one.

On the other hand,

To obtain an upper bound of equation (2.5), it is sufficient to assume the existence of an upper bound of the ratio of the above quantities, namely (omitting $(f^{-n}(p))$ to simplify notation)

We needed bars over $\unicode{x3bb} ,\nu ,a$ to reduce above a fraction to the summand 1. From now on these bars (integrals) are not needed.

We conclude calculations with sufficiency to assume the existence of an upper bound of

(2.6)

or to assume that the inverse

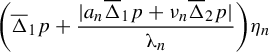
is bounded away from 0.

Thus, Lipschitz property follows from either of

(2.7) $$ \begin{align} \overline\Delta_1 p \; \eta_n \ge \operatorname{\mathrm{Const}}> 0 \end{align} $$

or

(2.8)

The condition equation (2.8), in the diagonal case $a_n=0$ , means that the contraction in the space of stable leaves $W^s$ by $f^{-n}$ , along the coordinate x, due to small $\eta _n^{-1}$ is strong enough to bound the twisting effect caused by $\log \nu _n /\log \unicode{x3bb} _n$ , which implies the Lipschitz continuity of all the holonomies at p along unstable foliation of a bounded length leaves (e.g. by $2\pi $ ). This is for $\overline \Delta _1(p)\approx 0$ (hence $\overline \Delta _2(p)$ large). Otherwise the Lipschitz condition holds automatically.

The condition equation (2.7) is equivalent to the strong locally Lipschitz equation (2.2) in Definition 2.5 by the transversality condition, see Remark 2.3 and equations (2.2) and (2.3). This implies that the distance between $W^s(f^{-n}(p))$ and $W^s(f^{-n}(q))$ is bounded by $\operatorname {\mathrm {Const}}\times \overline \Delta _1(p)$ so $\overline \Delta _1(q)\le \operatorname {\mathrm {Const}}\overline \Delta _1(p)$ so $d(q,q')\le \operatorname {\mathrm {Const}} d(p,p')$ so just Lipschitz property of $h_{p,q}$ at p.

By Remark 2.6 for Const above large enough, we obtain a strong bi-Lipschitz property.

We denote the set of all strong locally bi-Lipschitz points in $\Lambda $ by $L^s$ and $L^s\cap W^s(p)$ with $x(p)=x$ by $L^s_x$ . Sometimes we write $\Lambda ^s(\tau , L,n )$ for specified n, see equation (2.2).

The following has already been mentioned in Theorem 2.8.

Lemma 2.9. $h_{x,x'}(L_x^s)=L^s_{x'}$ for all $x,x'\in S^1$ for the holonomy $h_{x,x'}$ along unstable foliation. The holonomy is locally Lipschitz on $L^s$ .

Notation 2.10. We call the set complementary to $L^{s}$ in $\Lambda $ weak non-Lipschitz, and denote it by $NL^w$ . By Lemma 2.8, this condition is weaker than non-Lipschitz. It includes some Lipschitz (e.g. if the bunching condition holds, see Theorem 1.6).

Later on, we shall need the following fact easily following from the definitions.

Lemma 2.11. For every $p\in L^s$ , there exists n such that

$$ \begin{align*}W^{ss}(p)\cap\Lambda\cap H_n(p)=\{p\}. \end{align*} $$

Proof Notice that the existence of $p'\in W^{ss}(p)\cap \Lambda \cap (H_n(p)\setminus H_{n+1}(p))$ is equivalent to $\pi _{x,y}(f^{-(n+1)}(p))\in \Gamma $ . If it happens for n arbitrarily large, it contradicts $p\in L^s$ .

3 Lipschitz versus geometric measure

Definition 3.1. Let $t=t_0$ be the only zero of the pressure function $t\mapsto P(f^{-1}, t\log (\unicode{x3bb} ' \circ f^{-1}))$ . Since $\unicode{x3bb} '<1$ , this function is strictly decreasing from $+\infty $ to $-\infty $ . Denote by $h^*$ the entropy of the equilibrium measure $\mu =\mu _{t_0}$ for the potential $t_0\log (\unicode{x3bb} \circ f^{-1})$ (called also stable SRB-measure, see §1).

A geometric meaning of this is that for an arbitrary $W^s$ , replacing $\unicode{x3bb} '$ by a function having logarithm cohomologous to $\log \unicode{x3bb} '$ (denote it also by $\unicode{x3bb} '$ ), not depending on future $(|i_1,\ldots )$ , the quantities $\log \unicode{x3bb} _n (f^{-n}(p))$ for $p=\rho (\ldots i_0|i_1,\ldots )$ are approximately diameters of $f^n(W^s(f^{-n}(p)))$ provided $\nu ' < \unicode{x3bb} '$ . The quantity $t_0$ , which would be Hausdorff and box dimensions in the conformal case, here, in the non-conformal case, is only the upper bound of the dimensions of $W^s\cap \Lambda $ , so-called ‘affinity dimension’, [8]. The aim of this and the next sections is to prove that $t_0$ is in fact the Hausdorff dimension of all $W^s\cap \Lambda $ .

We start now with the following.

Definition 3.2. For each ${\underline i}=(i_{-n},\ldots ,i_0)$ , define

$$ \begin{align*} h_n({\underline i})&:= \frac1{n}\log\#\bigg\{(i_1,\ldots,i_n): \widehat H_{i_{-n},\ldots,i_0 |} \cap B(\widehat V_{|i_1,\ldots,i_n}, L_1 {\eta}^{-1}_n( \pi_x \rho({\underline i})))\\ &\qquad\qquad\quad \cap \bigcup_{i^{\prime}_n,\ldots,i^{\prime}_0 \not=i_0}\widehat H_{i^{\prime}_{-n},\ldots,i^{\prime}_0 |} \not=\emptyset \bigg\}, \end{align*} $$

where $L_1$ is the constant from Theorem 2.8. Define also

(3.1) $$ \begin{align} h_n:=\sup h_n({\underline i}) \;\;\;\; \mathrm{and}\;\;\;\; h:=\limsup h_n. \end{align} $$

Similarly the following.

Definition 3.3. For infinite $\underline i=(\ldots ,i_{-n},\ldots ,i_0|)$ and $H_{\underline {i} }=W^u(p)$ for $p\in \rho (\underline {i})$ ,

$$ \begin{align*} h^\infty_n({\underline i}):= \frac1{n}\log\#\{(i_1,\ldots,i_n): \widehat H_{\underline{i}}\cap \widehat V_{| i_1,\ldots,i_n} \cap B(\Gamma\cap \widehat H_{\underline{i}}, L_1 {\eta}^{-1}_n( \pi_x \rho({\underline i})) ) \not=\emptyset\}, \end{align*} $$

compare equation (2.2), and

(3.2) $$ \begin{align} h^\infty_n:=\sup h^\infty_n({\underline i}) \;\;\;\; \mathrm{and}\;\;\;\; h^\infty:=\limsup h^\infty_n. \end{align} $$

The following follows easily from the definitions and the transversality assumption.

Proposition 3.4. $h^\infty $ and h are independent of $L_1$ large enough. Moreover $h^\infty \le h$ . The opposite inequality also holds if $\sup \unicode{x3bb} '< 1/ \sup \eta '$ and $\nu '(p)<\unicode{x3bb} '(p)$ for every $p\in \Lambda $ , the property we name: uniform dissipation.

Lemma 3.5. Assume transversality and $\chi _{\mu _{t_0}}(\unicode{x3bb} '))< -\log \sup \eta '$ (call it half-uniform dissipation). Then

(3.3) $$ \begin{align} h^\infty <h^ *. \end{align} $$

Proof For an arbitrary $\varepsilon>0$ and n large enough, denoting by $\overline {\operatorname {\mathrm {BD}}}$ the upper box dimension, we easily get

(3.4) $$ \begin{align} h^\infty_n(\underline{i}) \le (\overline{\operatorname{\mathrm{BD}}}(\widehat H_{\underline{i} }\cap\Gamma)+\varepsilon ) ( \log \sup\eta'), \end{align} $$

for every $\underline i = \ldots ,i_0 |$ , that is, $W^u=W^u(p)$ for any $p\in \rho (\underline i)$ .

To prove this, we cover $W^u$ by pairwise disjoint (except their end points) arcs of the same length equal to $1/(\sup \eta ')^n$ (up to a constant) and use the definition of box dimension.

A difficulty we shall deal with below is, however, to pass in equation (3.4) to a uniform over $\underline {i}$ version, that is, with $\sup _{\underline i} h_n^\infty (\underline i)$ in equation (3.2).

Notice that

(3.5) $$ \begin{align} \overline{\operatorname{\mathrm{BD}}}(\widehat H_{\underline{i}}\cap\Gamma) \le t_0 &= h^*/(-\chi_{\mu_{t_0}}(\unicode{x3bb}'))\nonumber \\ &\le h^*/(-\sup\log\unicode{x3bb}') < h^* / \log \sup\eta'. \end{align} $$

The first inequality uses the ‘Lipschitz holonomy’ along (in fact only local) between an arbitrary $\widehat W^s$ and $\widehat W^u=\widehat W^u(p)$ . (Formally this is not even a holonomy, because of intersections of the leaves. However it is Lipschitz in the sense of varying all the lengths of the uniformly transversal sections of each strip $\widehat H_n$ for all n, by at most a common factor.) We shall prove it more precisely below.

Let $p'\in W^s \cap \Lambda $ be such that $p'=p'(\underline i')$ is the only point of the intersection $\rho (\underline i')\cap W^s$ . Assume that $i^{\prime }_0\not =i_0$ . Denote by $A(f)$ supremum over all $p,p'$ as above of the number of the intersection points of $\widehat W^u(p)$ and $\widehat W^u(p')$ . It is finite by the transversality assumption, see e.g. [14, Proposition 4.6].

For every $n\ge 0$ we have, due to $\nu <\unicode{x3bb} $ ,

for n large enough to kill a twisting effect which may be caused by ${\partial \nu }/{\partial y}$ . Hence, due to the transversality assumption,

for every component Comp of the intersection.

By the definition of $t_0$ we have, summing over all $(i^{\prime }_{-n},\ldots ,i^{\prime }_0|) $ with $i_0'\not =i_0$ ,

for $t>t_0$ and constant $C(t)$ or $t<t_0$ , respectively.

For each $r>0$ and $\widehat q\in \widehat W^u(p))\cap \Gamma $ , where $q\in \rho (\ldots ,i^{\prime }_0|)$ , find $n=n(q)$ the least integer such that the length satisfies $l(\widehat W^u\cap \widehat H_{i^{\prime }_{-n},\ldots ,i^{\prime }_0})\le r$ ; by the length (denoted above by diam) we mean here the length of the projection by $\pi _x$ to $\mathbb {R}$ (of course we can alternatively consider the lengths in $\widehat W^u(p)$ or $W^u(p)$ ).

Denote $\widehat W^u\cap \widehat H_{i^{\prime }_{-n},\ldots ,i^{\prime }_0}$ by $I(q,r)$ . Consider in $\widehat W^u$ the ball (arc) $J(q,r)=B(\widehat q,r)$ . Choose a family $J(q_k,r)$ of the arcs of the form $J(q,r)$ covering $\widehat W^u\cap \Gamma $ , having multiplicity at most 2, namely that each point in $\widehat W^u$ belongs to at most two arcs. Then $I(q_k,r)\subset J(q_k,r)$ for all k. On the other hand, by the definition of $n(q)$ , there is a constant K such that $K l(I(q_k,r))\ge l(J(q_k,r))$ .

Finally notice that for two different $q_k$ and $q_{k'}$ , it may happen that $n=n(k)=n(k')$ and the nth codings $i_{-n},\ldots ,i_0$ are the same; in other words, the nth horizontal cylinders coincide. Then however, $J(q_k)$ and $J(q_{k'})$ intersect so the coincidence of these codings may happen only for at most two different k and $k'$ .

Thus, for all $t>t_0$ ,

(3.6)

Hence, as our estimates hold for every $r>0$ , we obtain the first inequality in equation (3.4)

$$ \begin{align*}\overline{\operatorname{\mathrm{BD}}}( W^u(p)\cap \Gamma) \le t_0. \end{align*} $$

This has been a Moran covering type argument.

Another variant of this proof would be to consider for each n the partition of $W^u$ into $d_n:= 2\pi /r_n$ arcs of length $r=r_n=1/([\sup {\eta '}^n]+1)$ and consider the family of those arcs which intersect $\Gamma $ . Denote them by $J_k$ . For each k, choose an arbitrary $q_k\in \Lambda $ such that $\widehat q_k \in J_k\cap \Gamma $ and $q_k$ belongs to some $\rho (\underline i')$ with $i_0\not =i^{\prime }_0$ . Then consider $I_k$ as above. Finally, notice that each interval $I_k$ , as shorter than $r_n$ for n large enough, can appear at most twice.

Finally, by equation (3.6), the estimate (3.4) is uniform, that is, n for which it holds is independent of $\underline i$ . Indeed, for each $\underline i$ and n, we obtain for $r=1/(\sup \eta ')^n$ , denoting $\varepsilon =2(t-t_0)$ ,

$$ \begin{align*}(\exp n h_n^\infty(\underline i)) (2r)^{t_0+\varepsilon} \le (2r)^{\varepsilon/2}\operatorname{\mathrm{Const}} C(t)<1 \end{align*} $$

for n large enough.

So $h_n^\infty \le (t_0+\varepsilon )(\sup \eta ')$ for each $\varepsilon>0$ and n large enough, hence $h^\infty \le t_0 \sup \eta '$ . By equation (3.5), we have $h^*> t_0 \sup \eta '$ . Thus $h^\infty < h^*$ .

The simplest uniform dissipation, namely if ${\eta }^{-1}_n \equiv d^{-n}$ , provides the partitions of $S^1$ into arcs of equal lengths to be used in estimating BD. In more general cases, the partitions of $S^1$ into arcs between consecutive $\eta ^n$ preimages of a fixed point cause difficulties and a necessity to assume the half-uniform dissipation assumption using $\sup \eta '$ rather than $\eta '$ . They will be overcome in §4 in the proof of Theorem 4.1 by replacing h by certain $h^{\mathrm {{reg}}}$ by restricting in the definition to $\mu _{t_0}$ -Birkhoff regular points with respect to $\log \eta '$ , restricting $\Gamma $ .

Now, assuming the uniform dissipation, using $h<h^*$ following from Lemma 3.5 and Proposition 3.4, we can obtain the following.

Lemma 3.6. Assume that the transversality and the uniform dissipation condition (introduced in Proposition 3.4) hold. Then $\mu ^s_x(L^s)=1$ for $(\pi _x)_*(\mu )$ -a.e. $x\in S^1$ , where $\mu ^s_x$ are conditional measures of $\mu $ for the partition of $\Lambda $ into $W^s_x\cap \Lambda $ .

The same holds for all x, where $\mu ^s_x$ is $(h_{x',x})_*(\mu ^s_{x'})$ for $x'$ , where $\mu ^s_{x'}$ has already been defined as a conditional measure.

Remark that for $\mu $ -a.e. $p, p'$ the holonomy $h_{x,x'}$ for $x=\pi _x(p), x'=\pi _x(p')$ maps $\mu ^s_x$ to $\mu _{x'}^s$ , that is, $(h_{x,x'})_*(\mu ^s_x)=\mu ^s_{x'}$ .

Note that these measures coincide also with the factor measure $\mu ^-:= \Phi _*(\mu _{t_0})$ , where $\Phi $ maps the two sides to the one-sided shift to the right, on the space of sequences $(\ldots ,i_{-n},\ldots ,i_0)$ (projected to $f^{-1}$ by $\rho $ ). In fact, we can write $\mu $ in place of $\mu ^-$ considering its restriction to the $\sigma $ -algebra generated by horizontal cylinders.

Then the assertion of Lemma 3.6 says that $\mu ^-(\Phi (L^s))=\mu (L^s)=1$ .

Proof By the Shannon–McMillan–Breiman theorem [12] applied for $f^{-1}$ and by ergodicity, denoting as before by $H_n(p)$ the horizontal cylinder of level n containing p, we get

$$ \begin{align*}{1\over n+1}\log \mu( H_n(p))\to h^* \end{align*} $$

for $\mu $ -a.e. $p\in \Lambda $ , so for every $\varepsilon>0$ and n large enough,

(3.7) $$ \begin{align} \exp -(n+1)(h^* + \varepsilon) \le \mu(H_n(p)) \le \exp -(n+1)(h^* - \varepsilon). \end{align} $$

Given arbitrary $\varepsilon>0$ and n, denote the set of p values (a union of $H_n(p)$ values) where equation (3.7) does not hold, by $Y_{\varepsilon , n}$ . Thus, the irregular set

(3.8) $$ \begin{align} Y^{\mathrm{irreg}}_\varepsilon:=\limsup_{n\to\infty}Y_{\varepsilon,n}= \bigcap_n \bigcup_{k\ge n} Y_{\varepsilon,k} \end{align} $$

has measure $\mu $ equal to 0. Its $\varepsilon $ -regular complement $\liminf _{n\to \infty }X_{\varepsilon ,n}= \bigcup _n \bigcap _{k\ge n} X_{\varepsilon ,k}$ for $X_{\varepsilon .k}=\Lambda \setminus Y_{\varepsilon ,k}$ has full measure $\mu $ for each $\varepsilon $ .

Remark that for our Gibbs measure, we can use Birkhoff’s ergodic theorem for $f^{-1}$ and $\log \unicode{x3bb} '$ in place of the Shannon–McMillan–Breiman theorem:

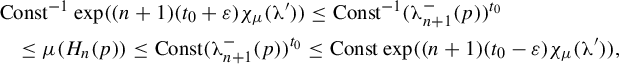$$ \begin{align*} &\operatorname{\mathrm{Const}}^{-1} \exp ((n+1)(t_0 + \varepsilon )\chi_\mu(\unicode{x3bb}') ) \le \operatorname{\mathrm{Const}}^{-1} (\unicode{x3bb}^-_{n+1} (p))^{t_0} \\ &\quad\le \mu( H_n(p))\le \operatorname{\mathrm{Const}} (\unicode{x3bb}^-_{n+1} (p))^{t_0}\le \operatorname{\mathrm{Const}} \exp ((n+1)(t_0-\varepsilon )\chi_\mu(\unicode{x3bb}') ), \end{align*} $$

where $\chi _{\mu }(\unicode{x3bb} ') =\int \log \unicode{x3bb} '\, d\mu $ .

Denote by the family of all horizontal cylinders $H_{2n}$ , whose $\pi _{x,y}$ -projections $\widehat H_{2n}$ have ‘horizontal extensions’ to $(-L2\pi , (L+1)2\pi )$ intersecting $\widehat f^n( \Gamma )$ and else which are in $X_{\varepsilon ,2n}$ . The constant L is the one that appeared in equation (2.2).

Claim 3.7. The upper bound of is roughly $\exp (n h + (n+1)h^*)$ (‘roughly’ means: up to a factor of order at most $\exp n\varepsilon $ ).

Indeed, the number $\exp n h$ comes from $f^n(H)$ for each $H\in H(n)$ , more precisely from $\widehat {f}^n$ -images of the rectangles $\widehat H\cap \widehat V_{|i_1,\ldots ,i_n}$ counted in Definition 3.2. The number $\exp (n+1)h^*$ comes from the number of ‘regular’ $H\in H(n)$ roughly as in equation (3.7), that is, being $f^{n+1}$ -images of ‘regular’ $V_n$ . More precisely, of those H values for which some $H_{2n+1}\subset f^n(H)$ are in $X_{\varepsilon ,2n+1}\cap X_{\varepsilon ,n}$ . (Notice that this does not depend on the choice of $H_{2n+1}$ , due to equation (3.9). Notice also that H satisfying this, need not exhaust all H satisfying equation (3.7).) The measure $\mu $ of each such H is lower bounded for $p\in H$ by

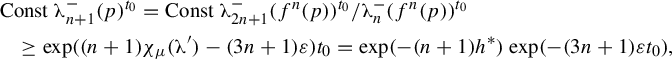(3.9) $$ \begin{align} &\operatorname{\mathrm{Const}} \unicode{x3bb}^-_{n+1}(p)^{t_0} = \operatorname{\mathrm{Const}} \unicode{x3bb}^-_{2n+1}(f^n(p))^{t_0} / \unicode{x3bb}^-_n(f^n(p))^{t_0} \nonumber\\ &\quad\ge \exp ((n+1) \chi_\mu(\unicode{x3bb}')-(3n+1)\varepsilon)t_0 = \exp (- (n+1) h^*) \exp (- (3n+1) \varepsilon t_0 ), \end{align} $$

due to chain rule $f^{-(n+1)}(p) = f^{-2n+1} (f^n(p)) \circ f^n(p)$ , compare equation (4.4), and Gibbs property of $\mu $ (used already above to reformulate equation (3.7) to the language of $\unicode{x3bb} '$ ).

The number of our ‘regular’ $H_n$ values is bounded by the reciprocal of the bound in equation (3.9). Thus,

The claim has been proven.

Thus,

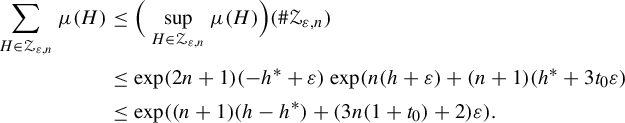
So, for an arbitrary $\varepsilon>0$ small enough,

so $\mu (NL^w)=0$ , see Notation 2.10.

4 Hausdorff dimension

Theorem 4.1. (Theorem 1.2)

Assume $\chi _{\mu }(\nu ')<\chi _{\mu } (\unicode{x3bb} ')< -\chi _{\mu }(\eta ')$ . Then, for $\operatorname {\mathrm {HD}}$ denoting the Hausdorff dimension, for $\Lambda _x$ denoting $\Lambda \cap (\{x\}\times \mathbb {D})=\Lambda \cap W^s_x$ :

1. (1) $\operatorname {\mathrm {HD}}(\Lambda _x)=t_0$ for every x; and

2. (2) $\operatorname {\mathrm {HD}}(\Lambda )=1+t_0$ , where $t_0= {h^*/-\chi _{\mu _{t_0}}(\unicode{x3bb} ')}$ .

First, we prove this theorem under stronger assumptions.

Theorem 4.2. (Theorem 1.2, uniformly dissipative setting)

Assertions of Theorem 4.1 hold if $\sup \unicode{x3bb} ' < 1/\sup \eta '$ .

We start with a general (not only in the uniformly dissipative) case.

Lemma 4.3. For every $p\in \Lambda $ , all $r>0$ and balls (discs) $B^s$ in the stable manifold $W^s_{\pi _x(p)}$ ,

$$ \begin{align*}\mu^s_{\pi_x(p)}(B^s(p,r)) \ge \operatorname{\mathrm{Const}} (\operatorname{\mathrm{diam}} B^s(p,r))^{ t_0}. \end{align*} $$

In particular,

$$ \begin{align*}\liminf_{r\to 0} {\log\mu^s_{\pi_{x(p)}}(B^s(p,r)) \over \log \operatorname{\mathrm{diam}} (B^s(p,r))}\le t_0. \end{align*} $$

One can even replace liminf by limsup.

Proof Lemma 4.3 follows from

(4.1)

One uses the definition of $\mu ^s$ (Gibbs property) and the fact that the diameter of each $B^s(p,r)$ is comparable to $\unicode{x3bb} _n(f^{-n}(p))$ , by bounded distortion. The conditional measures $\mu ^s$ were discussed after the statement of Lemma 3.6.

More sophisticated is the opposite inequality.

Lemma 4.4. For $\mu $ -a.e. $p\in \Lambda $ , the local dimension satisfies

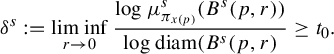$$ \begin{align*}\delta^s:=\liminf_{r\to 0} {\log\mu^s_{\pi_{x(p)}}(B^s(p,r)) \over \log \operatorname{\mathrm{diam}} (B^s(p,r)}\ge t_0. \end{align*} $$

Proof One uses the Ledrappier–Young formula [10]

$$ \begin{align*}h_\mu(f)=\delta^{ss} (-\chi_{\mu}(\nu')) + (\delta^s-\delta^{ss}) (-\chi_\mu(\unicode{x3bb}')) \end{align*} $$

and the fact that $\delta ^{ss}=0$ since for $p\in L^s$ the local manifold $W^{ss}$ consists only of the point p, see Lemma 2.11. Remember also, Lemma 3.6, that $\mu _x^s(L^s)=1$ for all $x\in S^1$ , so $\mu (L^s)=1$ . Hence,

$$ \begin{align*}h_\mu(f)=\delta^{s} (-\chi_{\mu}(\unicode{x3bb}')),\; \; \mathrm{so} \; \delta^s= h_\mu(f)/-\chi_\mu(\unicode{x3bb}')= t_0.\\[-36pt] \end{align*} $$

Proof of Theorem 1.2, uniformly dissipative setting Step 1. $\operatorname {\mathrm {HD}}(\Lambda _x)=t_0$ for every x follows from Lemmas 4.3 and 4.4 and from Frostman Lemma, see [12, Theorem 8.6.3].

Step 2. Since by Lemma 3.5 and Proposition 3.4 $h<h^*:=h_{\mu _{t_0}}(f)$ , we know by Lemma 3.6 that there exists x (in fact for all x) $\mu ^s_x(L^s)=1$ . By Lemma 2.9, all the holonomies $h_{x,x'}$ for $0\le x'\le 2\pi $ are locally bi-Lipschitz on $L^s(x)$ . Change the coordinates on $\Lambda $ by $F(x', y, z):= (x',h_{x,x'}^{-1}(y,z))$ , mapping $\Lambda $ to the cartesian product $[0,2\pi ) \times \Lambda \cap W^s_x$ . Then this change is locally Lipschitz on $\bigcup _{0\le x' \le 2\pi }h_{x,x'}(L^s_x)=L^s$ . Hence, $\operatorname {\mathrm {HD}}(\Lambda )\ge \operatorname {\mathrm {HD}}(L^s)=1+HD(L^s_x)= 1+t_0$ .

More precisely, F is locally Lipschitz, in the sense that there exists $L>0$ such that for every $p\in L^s$ , there exists measurable $r(p)>0$ such that for every $r\le r(p)$ and $q\in B(p,r)$ , $\operatorname {\mathrm {dist}} (F(p), F(q)) \le L \operatorname {\mathrm {dist}} (p,q)$ . This is sufficient to not increase dimension by splitting the space into a countable number of pieces.

Step 3. The opposite inequality is implied by Lemma 4.3. Indeed, notice that for every $r=\unicode{x3bb} _n(p)$ and $x'\in B(x(p), r)$ , we have

$$ \begin{align*}\{x'\} \times B^s(\pi_{y,z}(p), (C+1)\cdot r)\supset h_{x(p),x'}(B^s(\pi_{y,z},r), \end{align*} $$

where $C:= \tan \measuredangle (E^u,E^s)$ . Hence

$$ \begin{align*}\mu^s(\{x'\} \times B^s(\pi_{y,z}(p), (C+1)\cdot r))\ge \mu^s h_{x(p),x'}(B^s(\pi_{y,z},r). \end{align*} $$

Hence, for

(4.2) $$ \begin{align} \widehat\mu:=d\mu^s_x d\operatorname{\mathrm{Leb}}_1(x), \end{align} $$

for every $p\in \Lambda $ ,

and in conclusion, $\widehat \mu (B(p,Cr))\ge \operatorname {\mathrm {Const}} r^{1+t_0}$ yielding the required upper estimate $\operatorname {\mathrm {HD}}(\Lambda )\le 1+t_0$ .

Definition 4.5. A point $p=\rho (\ldots i_{-n},\ldots ,i_0,\ldots ,i_n,\ldots )\in \Lambda $ is said to be Birkhoff $(\xi , \varepsilon , N)$ -backward regular for an arbitrary $\varepsilon>0$ and for $\xi =\nu ,\unicode{x3bb} $ or $\eta $ , if for all $n\ge N$ ,

(4.3) $$ \begin{align} \exp n(\chi_\mu(\xi)-\varepsilon) \le \xi_n^-(p)) \le \exp n(\chi_\mu(\xi)+\varepsilon)), \end{align} $$

see Notation 2.4.

Analogously $p\in \Lambda $ is said to be Birkhoff $(\xi , \varepsilon , N)$ -forward regular if the above estimates hold for $\xi _n^+(p)$ in place of $\xi _n^-(p)$ .

When we mean just equation (4.3), we say $(\xi , \varepsilon , n)$ -forward (backward) regular, omitting “Birkhoff”. Compare the Shannon–McMillan–Breiman property in the proof of Lemma 3.6.

By bounded distortion, the property (4.3) for $p=\rho (\ldots i_{-n},\ldots ,i_0,\ldots ,i_n,\ldots )$ depends only on $(i_{-n},\ldots ,i_0)$ , provided we insert constant factors before exp, so it can be considered as a property of a horizontal cylinder $H_n$ . Analogously for the forward regularity, this is a property of vertical cylinders $V_n$ . We call these cylinders $(\xi , \varepsilon , n)$ -forward or backward regular, and all other points or level n cylinders irregular.

Proof of Theorem 1.2. We shall modify (generalize) the definition of irregular sets $Y_{\varepsilon ,n}$ in Lemma 3.6 and follow the strategy of the proof of that lemma.

Recall the notation $\xi _n^-(p):= \xi _n(f^{-n}(p))$ . Notice that for all integers $m>0$ ,

(4.4) $$ \begin{align} \xi_m^-(f^{-n}(p) = \xi_{n+m}^-(p) / \xi_{n}^-(p), \end{align} $$

so for p being $(\xi ,\varepsilon , k)$ -backward regular for $k=n$ and $k=n+m$ , we have

$$ \begin{align*} &\exp (n+m)(\chi_\mu(\xi)-\varepsilon)) / \exp n(\chi_\mu(\xi)+\varepsilon)) \le \xi_m^-(f^{-n}(p) \\[-3pt] &\quad\le \exp (n+m)(\chi_\mu(\xi)+\varepsilon)) / \exp n (\chi_\mu(\xi)-\varepsilon)). \end{align*} $$

Hence

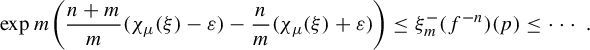(4.5) $$ \begin{align} \exp m \bigg(\frac{n+m}m (\chi_\mu(\xi)-\varepsilon) - \frac{n}m (\chi_\mu(\xi)+\varepsilon)\bigg) \le \xi_m^-(f^{-n})(p)\le \cdots. \end{align} $$

Hence

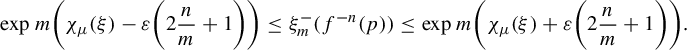(4.6) $$ \begin{align} \exp m \bigg(\chi_\mu(\xi)-\varepsilon\bigg(2\frac{n}m + 1\bigg)\bigg) \le \xi_m^-(f^{-n}(p)) \le \exp m \bigg(\chi_\mu(\xi)+\varepsilon\bigg(2\frac{n}m + 1\bigg)\bigg). \end{align} $$

For each $n,m\in \mathbb {N}$ denote by $X_{\varepsilon ,n,m}$ the union of all $H_{n+m}$ horizontal cylinders of $(\xi ,\varepsilon ,n)$ -backward regular points in $\Lambda $ for all $\xi =\nu ,\unicode{x3bb} $ and $\eta $ , and yet $(\unicode{x3bb} ,\varepsilon ,n+m)$ -backward regular.

Write also $Y_{\varepsilon ,n,m}:=\Lambda \setminus X_{\varepsilon ,n,m}$ for irregular sets. Now, as in §3, in the proof of Lemma 3.6, the idea is to remove (due to the uniform dissipation assumption, we needed to remove there less than here) for each n the irregular set $Y_{\varepsilon ,n,m}$ for m to be defined later on, and estimate the number of remaining cylinders $H_{n+m}$ , which are regular contaminated by other regular cylinders in the sense below in equation (4.7).

A point (and cylinder) $p\in H_{n+m}$ regular as above is said to be $(\Gamma ^{\operatorname {\mathrm {reg}}}_{n,m})$ -contaminated if for ${\tilde p}:=f^{-n}(p)$

(4.7) $$ \begin{align} \pi_{x,y}({\tilde p})\in B^u(\Gamma^{\operatorname{\mathrm{reg}}}, L_1 {\eta}^{-1}_n(\tilde p)), \end{align} $$

compare Definition 2.5. Here $B^u$ denotes a ball in ${\widehat W}^u(\tilde p)$ . The set $\Gamma ^{\operatorname {\mathrm {reg}}}$ is defined as $\Gamma $ in Definition 2.2, but restricted to $\widehat p$ being a $\pi _{x,y}$ image of $q=\rho (\ldots ,i_0|)$ and $q'=\rho (\ldots ,i^{\prime }_0|)$ such that $f^n(q)$ and $f^n(q')$ are in $X_{\varepsilon ,n,m}$ .

As in Definition 2.5, we can say equivalently that $\widehat V_n(\tilde p)$ is $\Gamma ^{\operatorname {\mathrm {reg}}}_{n,m}$ -contaminated if it does not satisfy equation (2.2), with $\Gamma $ replaced by $\Gamma ^{\operatorname {\mathrm {reg}}}_{n,m}$ . We can say also that the rectangle $\widehat H_m \cap \widehat V_n$ is contaminated, as in Definition 3.2. See also §7.4.

Here it is comfortable to look for $m>0$ as small as possible so that

(4.8) $$ \begin{align} \unicode{x3bb}^-_m(f^{-n}(p) < (\eta^-_n(p))^{-1}, \end{align} $$

compare equation (5.3) later on. Taking into account that both $f^n(q)$ and q are in $X_{\varepsilon ,n,m}$ , we obtain using equation (4.6) the sufficient condition

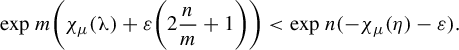$$ \begin{align*}\exp m \bigg(\chi_\mu(\unicode{x3bb})+\varepsilon\bigg(2\frac{n}{m} + 1\bigg)\bigg) < \exp n (-\chi_\mu(\eta)-\varepsilon). \end{align*} $$

It follows that for $\epsilon>0$ small, it is sufficient

(4.9) $$ \begin{align} m/n \approx \chi_\mu(\eta')/(-\chi_\mu(\unicode{x3bb}')) + \varepsilon' \end{align} $$

with $\varepsilon '>0$ also small.

Summarizing: for given $H_m(\tilde p)$ with $p=f^n(\tilde p)\in X_{\varepsilon ,n,m}$ , we define $h^{\operatorname {\mathrm {reg}}}_n:=1/({n+1})\log Z_n$ , where $Z_n$ is the number of $\Gamma ^{\operatorname {\mathrm {reg}}}_{n,m}$ -contaminated $\widehat V_n$ in $\widehat H_m(\tilde p)$ (by $H_m(\tilde q)$ with the $i_0$ symbols different from that for $H_m(\tilde p)$ , with $q=f^n(\tilde q)\in X_{\varepsilon ,n,m}$ ).

The number $Z_n$ is bounded by a constant times the number of $H_m$ above, taking into account L in equation (2.2) and the observation that regular $H_m$ , as ‘thinner’ than $V_m$ , can intersect at most two (neighbour) $V_m$ values.

Hence

$$ \begin{align*}\exp n h^{\operatorname{\mathrm{reg}}}_n \le \operatorname{\mathrm{Const}} \exp m h^*, \end{align*} $$

so using equation (4.9),

(4.10) $$ \begin{align} h^{\operatorname{\mathrm{reg}}}\le h^* (\chi_\mu(\eta')/(-\chi_\mu(\unicode{x3bb}'))) + \varepsilon'. \end{align} $$

The rest of the proof repeats the proof of Theorem 4.2.

In particular, by Birkhoff ergodic theorem for an arbitrary $\varepsilon{\kern1pt>\kern1pt}0$ , $\mu (\lim \sup _{n\to \infty }\! Y_{\varepsilon ,n}){\kern1pt=\kern1pt}0$ and the complementary set in $NL^w$ , for $\varepsilon>0$ small enough, where $h^{\operatorname {\mathrm {reg}}}<h^*$ , has measure $\mu $ also equal to 0.□

The above proof finishes also the proof of Theorem 1.6 in the general setting, saying that $\mu _x^s(NL^w)=0$ , compare Lemma 3.6 in the uniform dissipation case. Compare also equation (3.8).

5 Packing measure

For the definition of packing measure, we refer the reader to [12, §8.3]. Denote packing measure in dimension t by $\Pi _t$ .

We shall prove the following.

Theorem 5.1. Under the assumptions of Theorem 4.1 (Theorem 1.2), namely if

$$ \begin{align*}\chi_{\mu}(\nu')<\chi_{\mu} (\unicode{x3bb}')< -\chi_{\mu}(\eta'), \end{align*} $$

for the Gibbs measure $\mu =\mu _{t_0}$ on $\Lambda $ , then for every $p\in \Lambda $ , it holds that

(5.1) $$ \begin{align} 0<\Pi_{t_0}(W^s(p)\cap \Lambda)<\infty. \end{align} $$

Moreover, the density $d\Pi _{t_0}/d\mu ^s_{t_0}$ is positive $\mu ^s_{\pi _x(p)}$ almost everywhere (recall that $\mu ^s_{\pi _x(p)}$ is the conditional measure on $W^s(p)$ ).

Also,

(5.2) $$ \begin{align} 0<\Pi_{1+t_0}(\Lambda)<\infty \end{align} $$

and moreover $d\Pi _{t_0+1}/d\mu _{t_0}$ is positive $\mu _{t_0}$ almost everywhere on $\Lambda $ .

This generalizes the analogous theorem proved for linear solenoids in [17].

Proof Step 1. Regular contaminated rectangles. Given an arbitrary $\varepsilon>0$ , denote by $\mathcal {H}(\varepsilon ,t)$ the union of all $H_t$ containing points in $\Lambda $ satisfying the backward regularity condition in equation (4.3) for t (denoted there n) and $\xi =\unicode{x3bb} ,\nu $ .

Analogously, denote by the union of all $V_t$ containing points in $\Lambda $ satisfying the forward regularity condition analogous to equation (4.3) for t (denoted there by n) and $\xi =\eta $ and by .

We sometimes call $H_t$ and $V_t$ as above, just regular.

Consider an arbitrary $m\in \mathbb {N}$ and given $\varepsilon>0$ , define $n=n(\varepsilon ,m)$ as the biggest integer n such that, compare equations (4.9) and (4.8),

(5.3) $$ \begin{align} \frac{n}{m} \le \frac{-(\chi_\mu (\unicode{x3bb}')-\varepsilon)}{\chi_\mu(\eta')+\varepsilon}. \end{align} $$

We consider $\varepsilon $ small enough that the latter fraction is bigger than 1.

Later on, we shall consider an arbitrary $\alpha : 0<\alpha \le 1$ and the integer $[\alpha n]$ in place of n (the square bracket means the integer part), sometimes writing just $\alpha n$ . Finally, we shall specify $\alpha $ . Of course, equation (5.3) is satisfied for $[\alpha n]$ in place of n.

Notice that for an arbitrary $(\unicode{x3bb} ,\varepsilon , m)$ -backward regular $p\in H_m\subset \mathcal {H}(\varepsilon ,m)$ , therefore for regular $H_m(p)$ ; the diameter of its intersection with any $W^s$ is at most $\exp ( m(1-\varepsilon )\chi _\mu (\unicode{x3bb} '))$ (up to a constant related to distortion).

For all $\underline i = (\ldots ,i_0|)$ , writing $\rho (\underline i)=W^u(\underline i)=W^u$ , we obtain the uniform (over $\underline i$ ) estimate (3.4) on $h_n^\infty (\underline i)$ as in Lemma 3.5 for $W^u$ restricted to the intersection with . We write $h_n^{\infty , \operatorname {\mathrm {reg}}}(\underline i)$ .

Indeed, we can then use, for every forward regular $V_n$ , the property $\operatorname {\mathrm {diam}} (W^u\cap V_n) \ge \exp -n(\chi _\mu (\eta ')+\varepsilon )$ . (We accept that one $\varepsilon $ can differ from another if it does not lead to a confusion.) In equation (3.5), we use then $\chi _\mu (\unicode{x3bb} ')< -(\chi _\mu (\eta ')+\varepsilon )$ .

Defining $h^{\infty ,\operatorname {\mathrm {reg}}}:=\lim _{n\to \infty } \limsup _{\underline i} h_n^{\infty , \operatorname {\mathrm {reg}}}$ analogously to Definition 3.3, we get for $\varepsilon $ small enough

$$ \begin{align*}h^{\infty,\operatorname{\mathrm{reg}}}<h^*. \end{align*} $$

We obtain the same estimates, in particular $h^{\operatorname {\mathrm {reg}}}<h^*$ , if in place of $W^u$ , thicken it to $H_m$ restricting ourselves to backward regular $p\in H_m\subset \mathcal {H}(\varepsilon , m)$ , because then, if $p\in V_{[\alpha n]}$ backward regular, for $n=n(\varepsilon ,m)$ ,

$$ \begin{align*}\operatorname{\mathrm{diam}} \pi_{x,y} (H_m(p) \cap W^s) \ll \operatorname{\mathrm{diam}} \pi_{x,y}(V_{[\alpha n]}(p) \cap W^u) \end{align*} $$

due to

$$ \begin{align*}\exp m(\chi_\mu(\unicode{x3bb}')+\varepsilon) < \exp -[\alpha n](\chi_\mu(\eta')+\varepsilon), \end{align*} $$

see Definition 3.2 and the transversality.

In words, the number of forward regular vertical cylinders $V_{[\alpha n]}$ , whose $\pi _{x,y}$ projections $\widehat V_{[\alpha n]}$ intersect the ‘rhombs’ $\widehat H_m(p)\cap \widehat H^{\prime }_m$ with $H^{\prime }_m=\rho (i^{\prime }_{-m},\ldots ,i^{\prime }_0)$ , $i^{\prime }_0\not =i_0$ as in Definition 3.2 widened by their $L_1$ th neighbours in $\widehat H_m(p)$ , is bounded by $\exp {[\alpha n]} (h^{\operatorname {\mathrm {reg}}}+2\varepsilon )$ . This estimate is uniform over our regular $H_m$ values.

Then their union denoted by has measure $\mu $ upper bounded by

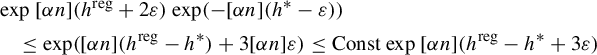(5.4) $$ \begin{align} &\exp {[\alpha n]} (h^{\operatorname{\mathrm{reg}}} +2\varepsilon) \exp(- {[\alpha n]} (h^*-\varepsilon))\nonumber \\ &\quad\le \exp ( {[\alpha n]} (h^{\operatorname{\mathrm{reg}}}-h^*)+3 {[\alpha n]} \varepsilon)\le \operatorname{\mathrm{Const}} \exp {[\alpha n]} (h^{\operatorname{\mathrm{reg}}}-h^*+3\varepsilon) \end{align} $$

again uniformly for regular $H_m$ values, and for m large enough, exponentially decreasing as $m\to \infty $ , for $\varepsilon $ small enough.

By the Gibbs property, the same estimate holds for conditional measure $\mu $ in $H_m$ , namely , or just for $\mu $ restricted to $H_m$ , summed over regular $H_m$ values.

Step 2. Close cylinders. We keep $n, m$ and arbitrary $\alpha \le 1$ as above and consider an arbitrary integer $0<k\le m$ . We take care of intersections of $\widehat H_m$ with $\widehat H^{\prime }_m$ values with $i_{-k}\not =i^{\prime }_{-k}$ but $i_t=i^{\prime }_t$ for all $t=0,\ldots ,-(k-1)$ . Consider $f^{-k}(H_m)$ as one of the summands of the union

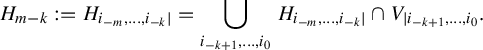$$ \begin{align*}H_{m-k}:=H_{i_{-m},\ldots,i_{-k} |}=\bigcup_{i_{-k+1},\ldots,i_0} H_{i_{-m},\ldots,i_{-k} |}\cap V_{| i_{-k+1},\ldots,i_0}. \end{align*} $$

By the estimate in Step 1 for $m-k$ , we cover the union of intersections $\widehat H_{m-k} \cap \widehat H^{\prime }_{m-k}$ with margins by a family of $\pi _{x,y}$ -projections of $V_{\alpha n(\varepsilon ,m-k)}$ values being $(\eta ,\varepsilon , [\alpha n(\varepsilon ,m-k))]$ -forward regular, leaving aside the part covered by irregular vertical ones, for $H_{m-k}$ backward regular. The union of this family has $\mu $ -conditional measure in $H_{m-k}$ bounded by

$$ \begin{align*}\operatorname{\mathrm{Const}} \exp [\alpha n(\varepsilon,m-k)] (h^{\operatorname{\mathrm{reg}}}-h^*+3\varepsilon). \end{align*} $$

So, the union of these $H_{m-k}\cap V_{[\alpha n(\varepsilon , m-k)]}$ values has exponentially shrinking measure $\mu =\mu _{t_0}$ for each m and for $m-k$ growing from $m_0$ to m. So the sums over $k=0,\ldots ,m-m_0$ are bounded by a constant independent of m, say by $\tfrac 12$ . By f-invariance of $\mu $ , the same bound by $\tfrac 12$ holds for $\bigcup _{k=0,\ldots ,m-m_0} f^{k}(\mathscr {R}(m,k))$ , where $\mathscr {R}(m,k)$ is the union of all regular $H_{m-k}\cap V_{[\alpha n(\varepsilon , m-k)]}$ above.

By construction, all $f^k(H_{m-k}\cap V_{[\alpha n(\varepsilon , m-k)]})$ (regular and not regular) are unions of ‘rectangles’ $H_m\cap V_{[\alpha n]}$ because $[\alpha n(\varepsilon , m-k)]\le [\alpha n]$ . So their $f^{[\alpha n]}$ -images are unions of entire $H_{[\alpha n]+m}$ values.

The conclusion is that for each $m, n=n(\varepsilon ,m)$ , the union $\textbf {H}^{\mathrm {b}} (m, \operatorname {\mathrm {reg}})$ of all ‘regular’ (more precisely $f^{[\alpha n]+k}$ -images of regular, see also Step 3) $H_{m+[\alpha n]}$ values whose $\pi _{x,y}$ -projections intersect at most bounded number of others in the same $H_{[\alpha n]}$ , not only ‘regular’ $\widehat H^{\prime }_{m+[\alpha n]}$ values, together with the union of all ‘irregular’ ones, to be estimated in Step 3, has measure $\mu $ at least $\tfrac 12$ . (In the proof of Lemma 3.6 and in the proof of Theorem 4.1 (Theorem 1.2), we just removed irregular horizontal cylinders, with union given n of measure tending to 0 by Birkhoff ergodic theorem, and eventually with $\limsup _{n\to \infty }$ of measure 0. These unions could be even proven to be of exponentially decreasing measure $\mu $ if we referred to the large deviations Lemma 7.1. Here we have additional summing over k which makes these irregular unions of measure larger than a positive constant for all n and depending on n. If we removed them, we would risk removing everything.)

We write ‘bounded number’ rather than not intersecting at all, since we have not taken care of intersections of $\widehat H_{m-k}\cap \widehat H^{\prime }_{m-k}$ for $m-k< m_0$ , that is, after acting by $\widehat f^{\,k+[\alpha n]}$ , the intersections of $\widehat H^{\prime }_{m+[\alpha n]}$ and $\widehat H_{m+[\alpha n]}$ are ‘close neighbour’ cylinders with coding different at most on positions $-(m+[\alpha n]),\ldots , -(m+[\alpha n]-m_0)$ .

Step 3. Remote cylinders. We discussed above $\widehat H_{m+[\alpha n]}$ intersecting bounded number of $\widehat H^{\prime }_{m+[\alpha n]}$ values in the same $\widehat H^{\prime }_{[\alpha n]}$ . We do not know how to avoid intersections of $\widehat H_{m+[\alpha n]}$ and $\widehat H^{\prime }_{m+[\alpha n]}$ having $(i_{-[\alpha n]},\ldots ,i_0|)$ different from $(i^{\prime }_{-[\alpha n]},\ldots ,i_0'|)$ . However, for each $(\xi ,\varepsilon , [\alpha n])$ -backward regular for $\xi =\unicode{x3bb} ',\nu '$ and $p\in H:=H_{m+[\alpha n]}$ and $p'\in H':=H^{\prime }_{m+[\alpha n]}$ in different horizontal cylinders $H_{[\alpha n]}$ and in each $W^s_x$ ,

(5.5)

for arbitrary constant $C>0$ , $m,n$ large enough, $\varepsilon $ small, provided

$$ \begin{align*}\exp [\alpha n]\chi_\mu(\nu') \gg \exp (m+ [\alpha n]) \chi_\mu (\unicode{x3bb}'), \end{align*} $$

that is, we assume

(5.6) $$ \begin{align} \alpha< \frac{\chi_\mu(\eta')}{-\chi_\mu(\nu')+\chi_\mu(\unicode{x3bb}')}. \end{align} $$

Step 4. Irregular sets. Above ‘regular’ means: in $\bigcup _{0\le k\le m-m_0} f^{[\alpha n(\varepsilon ,m-k)+k}(\mathscr {R}(m,k))$ , that is, in $\textbf {H}_1(m,k,\operatorname {\mathrm {reg}}):=f^{[\alpha n(\varepsilon ,m-k)+k]} (\mathcal {H} (\varepsilon ,m-k))$ and in for all $k=0,\ldots ,m-m_0$ , and additionally not in $\textbf {H}_3(t, \operatorname {\mathrm {irreg}})$ for all t large enough, see below.

Denote the complementary ‘irregular’ sets in $\bigcup \{H_{m+[\alpha n(\varepsilon ,m)}\}$ by $\textbf {H}_1(m,k,\operatorname {\mathrm {irreg}})$ and $\textbf {H}_2(m,k,\operatorname {\mathrm {irreg}})$ .

Due to large deviations Lemma 7.2, see (7.1),

$$ \begin{align*}\mu ({\textbf{H}}_1 (m,k, \operatorname{\mathrm{irreg}})) \le \operatorname{\mathrm{Const}} \exp - (m-k)\tau \end{align*} $$

and

$$ \begin{align*}\mu ({\textbf{H}}_2 (m,k, \operatorname{\mathrm{irreg}})) \le \operatorname{\mathrm{Const}} \exp - [\alpha n(\varepsilon,m-k)]\tau \end{align*} $$

for a constant $\tau>0$ depending on $\varepsilon $ , and the functions $\unicode{x3bb} '$ and $\eta '$ .

When we take unions over $0\le k\le m-m_0$ , we obtain an upper bound for measure $\mu $ of the unions ${\textbf {H}}_i (m,\operatorname {\mathrm {irreg}})$ for $i=1,2$ of these ‘irregular’ $\bigcup \{H_{m+[\alpha n(\varepsilon ,m)}\}$ values by a small constant, say $\tfrac 18$ , for $m_0$ large enough, for each n (formally for each m, but then each n is counted by a bounded number of times).

Finally, we distinguish another irregular set in $\bigcup \{H_{m+[\alpha n(\varepsilon ,m)}\}$ , for each m large enough, namely the complement $\textbf {H}_3 (m, \operatorname {\mathrm {irreg}})$ of the set of all $(\xi , \varepsilon , m+[\alpha n)]$ -backward regular cylinders $H_{m+[\alpha n]}$ for $\xi =\nu $ and $\unicode{x3bb} $ . By Birkhoff ergodic theorem, we can assume that $\mu (\bigcup _{t>N}\textbf {H}_3 (t, \operatorname {\mathrm {irreg}})) <\tfrac 18$ . for N large enough (compare $\mu (\limsup _{n\to \infty }Y_{\varepsilon ,n})=0$ in the proof of Lemma 3.6).

Step 5. The conclusion in stable manifolds. Denote $\textbf {H}(m,\kern-1pt\operatorname {\mathrm {reg}})\kern-1pt:=\kern-1pt\textbf {H}^{\mathrm {b}}\kern-1.5pt\setminus\kern-1.5pt\bigcup _{i=1}^3\kern-1pt\textbf {H}_i(m,\kern-1pt\operatorname {\mathrm {irreg}})$ . To conclude the proof of our theorem, use now [17, Lemma 3] for the conditional measure $\mu _x^s$ on $W_x^s$ . It yields in our case that due to $\mu (\textbf {H} (m,\operatorname {\mathrm {reg}}))\ge \tfrac 12 - 3\cdot \tfrac 18=\tfrac 18$ for m large enough, hence $\mu ^s_x(\textbf {H} (m,\operatorname {\mathrm {reg}})\cap W^s_x)\ge \operatorname {\mathrm {Const}} \cdot \tfrac 18$ , for a positive measure $\mu _x^s$ subset $\textbf {W}$ of $W_x^s$ , for every $q\in \textbf {W}$ there is a sequence $m_j$ such that $H_{m_j+[\alpha n_j]}(q)\in \textbf {H}(m_j,\operatorname {\mathrm {reg}})$ . In particular, there is a sequence of ‘regular’ horizontal cylinders containing q of level tending to $\infty $ , whose $\pi _{x,y}$ -projections are each at most boundedly intersecting the family of projections of other horizontal cylinders of the same level, provided they are both in $H_{[\alpha n]}(q)$ .

Therefore, for $q\in \textbf {W}$ by Gibbs property, due to $\chi _\mu (\nu ')<\chi _\mu (\unicode{x3bb} ')$ , equation (5.6), and regularity, there is a sequence $r_j\searrow 0$ such that

(5.7) $$ \begin{align} \mu^s_x (B(q,r_j))\le C r_j^{t_0}. \end{align} $$

Hence $\Pi _{t_0}(\textbf {W})\ge \operatorname {\mathrm {Const}} C^{-1} \mu _x^s(\textbf {W})$ , see e.g. [12, Theorem 8.6.2].

The density $d\Pi _{t_0}/d\mu _x^s $ is positive $\mu $ almost everywhere since the set $\textbf {W}$ can be found of measure $\mu $ arbitrarily close to 1. This can be achieved by replacing the constants $\tfrac 12$ and $\tfrac 18$ by arbitrarily small positive constants, by increasing $m_0$ adequately. This increases the allowed bound of the multiplicity of intersections of $H_{m+[\alpha n]}$ values, thus increasing C.

Another variant of this part of the proof is to use ergodicity of f.

Finally, the existence of an upper bound of $d\Pi _{t_0}/d\mu _x^s $ , in particular finiteness of $\Pi _{t_0}(W^s\cap \Lambda )$ follows from the uniform boundedness from below of ${\mu ^s_x B(q,r)}/{r^{t_0}}$ for r small enough, see Lemma 4.3. We again refer to [12, Theorem 8.6.2].

Step 6. Packing measure in $\Lambda $ . To prove $0<\Pi _{1+t_0}(\Lambda )$ in equation (5.2), notice that for an integer $n_0$ and every $q\in \textbf {W}$ , every $k_j:=m_j+[\alpha n_j]$ , as at the beginning of Step 4, and every $p_1,p_2\in W^u(q)$ , we have the following inclusion of intervals:

$$ \begin{align*}\pi_{x,y} (H_{k_j+n_0}(q)\cap W^s_{\pi_x(p_1)}) \subset \pi_{x,y} (H_{k_j}(q)\cap W^s_{\pi_x(p_2)}), \end{align*} $$

provided $\operatorname {\mathrm {dist}}(p_1,p_2)<r^{\prime }_j$ , where $r^{\prime }_j:=\unicode{x3bb} _{k_j+n_0}^- (q)$ .

In words: each square of sides of order $r^{\prime }_j$ , namely

$$ \begin{align*}[\pi_x(p_1),\pi_x(p_2)] \times (\widehat H_{k_j+n_0}(p_1)\cap W^s_{\pi_x(p_1)}) \end{align*} $$

is a subset of a piece of $\widehat H_{k_j}(q)$ of length $r^{\prime }_j$ (along the x-axis), with vertical (along the y) sections of length of order $r_j$ , where $r_j:=\unicode{x3bb} ^-_{k_j} (q)$ .

Hence, for a ‘skew product’ $\widehat \mu $ as in equation (4.2),

$$ \begin{align*}\widehat\mu (B(p_1, \operatorname{\mathrm{Const}} r^{\prime}_j)\le \operatorname{\mathrm{Const}} r_j^{1+t_0}. \end{align*} $$

We used here the fact that for $\operatorname {\mathrm {Const}}>0$ small enough,

$$ \begin{align*}\pi_{x,y} (B(p_1, \operatorname{\mathrm{Const}} r^{\prime}_j)\cap W^s_{\pi_x(p_1)}) \subset \widehat H_{k_j+n_0}(p_1) \cap W^s_{\pi_x(p_1)}. \end{align*} $$

Applying Frostman lemma finishes the proof of the left-hand side inequality of equation (5.2). The right-hand side inequality follows from Lemma 4.3.

Remark 5.2. When we take the $f^k$ or $f^{n+k}$ image, the conditional measures stay the same by the f-invariance of $\mu $ .

The phenomenon which manifests and helps is the affinity of the mapping when we measure distances with respect to invariant measures after passing to conditional measures on unstable foliation.

Remark 5.3. Notice that in estimating from below the local dimension $\delta ^s$ of $\Lambda \cap W^s(p)$ for a.e. p, we referred to Ledrappier–Young formula, using $W^{ss}_{\textrm{loc}}(p)\cap \Lambda =\{p\}$ , Lemma 2.11.

In fact, we knew there only that $\widehat H_{2n}(p)$ did not intersect $\widehat H_{2n}(p')$ such that $H_{2n}(p')\subset H_{n-1}(p)\setminus H_n(p)$ , but we did not exclude the intersecting for $H_{2n}(p')\subset H_n(p)$ . To avoid intersections, we split $H_n(p)$ into $H_{n+1}(p)$ and the complement, splitting both into $H_{2(n+1)}$ and getting disjointness for $H_{2(n+1)}(p')\subset H_{n}(p)\setminus H_{n+1}(p)$ , and so, splitting $H_{n+1}(p)$ , $H_{n+2}(p)$ …. This allowed the local disjointness of $\widehat W^u$ values as in the preceding paragraph.

We coped with the disjointness of entire $\widehat H_n$ values in §5 on packing measure, but for each $W^u$ , the disjointness of the consecutive cylinders containing it has been proved only for a sequence of n values.

For a sequence of n values, multiple self-intersections happen, thus leading to a proof that Hausdorff measure of each $W^s\cap \Lambda $ in dimension $t_0$ is 0, see [17] in the affine case. See the next section.

6 Hausdorff measure

Theorem 6.1. For f like in Theorems 1.2 and 4.1, Hausdorff measure in dimension $t_0$ , denoted by $\mathrm {HM}_{t_0}$ on each $W^s_x$ , satisfies

(6.1) $$ \begin{align} \mathrm{HM}_{t_0}(W^s_x\cap \Lambda)=0, \end{align} $$

and

(6.2) $$ \begin{align} \mathrm{HM}_{1+t_0}(\Lambda)=0. \end{align} $$

Proof Two horizontal cylinders $H_{n,1}, H_{n,2}$ of level n are said to overlap if for each $x\in S^1$ the set $\widehat H_{n,1}\cap \widehat H_{n,2} \cap \widehat W^s_x$ is non-empty (remember that the ‘hat’ means the projection by $\pi _{x,y}$ ).

Such a pair exists. Indeed, take $W^u(p_1)$ and $W^u(p_2)$ for $p_1,p_2\in \Lambda $ so that their $\pi _{x,y}$ projections intersect at $\pi _{x,y}(p_1)=\pi _{x,y}(p_2)$ (such an intersection point exists, see [2]). Thicken them by $H_{k,1}, H_{k,2}$ and consider vertical $V_m$ containing $p_1$ and $p_2$ . If m is large enough, then $H_{k+m,1}:=f^m(H_{k,1})$ and $H_{k+m,2}:=f^m(H_{k,2})$ overlap.

Here, $H_{n,0}$ is said to have an order d overlap if there exist $H_{n,i}, i=1,\ldots ,d$ horizontal cylinders of order n such that for all $x\in S^1$ and $i=1,\ldots ,D$ ,

$$ \begin{align*}\widehat H_{n,0}\cap \widehat H_{n,i} \cap \widehat W^s_x \not= \emptyset. \end{align*} $$

Such a family exists for every d and some n. Indeed, suppose we found already $H_{n,0}$ having an order $d-1$ overlap with $H_{n,i}, i=1,\ldots ,d-1$ . Take $H_{n,d}$ with $i^{\prime }_0\not =i_0$ , the zero symbols for $H_{n,0}$ and $H_{n,d}$ , so that the intersection $\widehat H_{n,0}\cap \widehat H_{n,d} \cap \widehat W^s_x $ is non-empty, say contains a point $q=(x,y)$ . Then consider vertical $V_m$ whose $\pi _{x,y}$ projection contains q. Then as above, for m large enough, $f^m(H_{n,i}), i=0,1,\ldots ,d$ , is the required family. (Notice that the latter intersection contains a point in $\widehat \Lambda $ provided $q\in \widehat \Lambda $ ; however we shall not use this observation.)

Choose now an arbitrary Birkhoff forward regular $\tilde p\in H_{n,0}\cap \Lambda $ . Replace the overlapping cylinders $H_{n,i}, i=0,\ldots ,d$ by $H_{n+k,i}=f^k(H_{n,i}\cap V_k)$ for $V_k\ni p$ and k large, to use time convergences in Birkhoff ergodic theorem. So, for $p:=f^k(\tilde p)$ , we have for each $i=0,\ldots ,d$ , $H_{n+k,i}\cap W^s(p) \subset B^s(p,\operatorname {\mathrm {Const}}\unicode{x3bb} ^-_{n+k}( p))$ . This is so due to $\chi _\mu (\nu ') < \chi _\mu (\unicode{x3bb} ')$ since then $\nu ^-_k(p) \ll \unicode{x3bb} ^-_{n+k}(p)$ for all k large enough (depending on $\tilde p$ ). Therefore this property is forward invariant under f.

We conclude that for $r=\operatorname {\mathrm {Const}} \unicode{x3bb} ^-_{n+k}(p))$ for $x=\pi _x( p)$ , and adequate constant C,

(6.3) $$ \begin{align} \mu_x^s(B(p,r))\ge C (d+1) r^{t_0}. \end{align} $$

The set $A(d)$ of these p has positive measure $\mu $ and is invariant under holonomies $h_{x,x'}$ . Therefore, invoking also ergodicity of $\mu $ , equation (6.3) holds in every $W^s_x$ for $\mu ^s_x$ -a.e. $p\in W^s_x$ and $r=r(p,d)$ . If we consider $A= \bigcap _{d\in \mathbb {N}} ( \bigcup _{n\in \mathbb {N}}f^n( A(d)))$ , then using Frostman lemma, we prove equation (6.1) for $\Lambda $ replaced by A. Finally, use Lemma 4.3, by which for each x, for $A':=\Lambda \setminus A$ , $\mu ^s_x (A') =0$ implies $\mathrm {HM}_{t_0}(A')=0$ .

Similarly, compare the proof of Theorem 4.2, Step 3, one proves equation (6.2).

7 Final remarks

7.1 Large deviations

We refer to the following lemma, see e.g. [7, Theorem 1.1].

Lemma 7.1. (On large deviations)

Let $F:X\to X$ be an open distance expanding map of a compact metric space, see [12, §4.1]. Then, for any Hölder continuous potential $\Phi :X \to \mathbb {R}$ , let $\mu _\Phi $ denote the unique Gibbs invariant measure for $\Phi $ , see [4]. Consider arbitrary Hölder functions $\phi , \psi : X \to \mathbb {R}$ . Then, for every $t \in \mathbb {R}$ ,

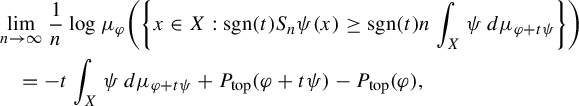$$ \begin{align*}\begin{aligned} &\lim_{n\to\infty}\frac1n \log\mu_\varphi\bigg(\bigg\{x\in X: \mathrm{sgn}(t)S_n \psi(x) \ge \mathrm{sgn}(t) n \int_X\psi\, d\mu_{\varphi+t\psi}\bigg\}\bigg) \\ &\quad= -t\int_X\psi\, d\mu_{\varphi+t\psi}+P_{\mathrm{top}}(\varphi+t\psi)-P_{\mathrm{top}}(\varphi), \end{aligned} \end{align*} $$

where by $P_{\mathrm {top}}$ we denote topological pressure, see e.g. [12].

Writing $\int \psi \, d\mu _{\varphi +t\psi }- \int \psi \, d\mu _{\varphi }:=\varepsilon $ , we can rewrite the above formula as follows:

$$ \begin{align*}\begin{aligned} &\lim_{n\to\infty}\frac1n \log \mu_\varphi\bigg(\bigg\{x\in X: \, \mathrm{sgn}(t)S_n \psi(x) \ge \mathrm{sgn}(t) n \bigg(\int\psi\, d\mu_{\varphi+t\psi} + \varepsilon\bigg)\bigg\}\bigg) \\ &\quad= -t\int_X\psi\, d\mu_{\varphi+t\psi}+P_{\mathrm{top}}(\varphi+t\psi)-P_{\mathrm{top}}(\varphi) := I(\pm\psi, \varepsilon). \end{aligned} \end{align*} $$

The latter $I(\varepsilon )$ measures the nonlinearity of $t\mapsto P_{\mathrm {top}}(\varphi +t\psi )$ .

A basic example of such F is $\varsigma :\Sigma _d^+\to \Sigma _d^+$ being the left shift map on the one-sided shift space with the standard metric $\operatorname {\mathrm {dist}}(\underline i,\underline i')=\sum _{n\in \mathbb {N}}|i_n-i^{\prime }_n|d^{-n}$ .

Symmetrically, one considers the right shift map $\varsigma ^{-1}:\Sigma ^-_d\to \Sigma ^-_d$ on the space of sequences $(\ldots ,i_n,\ldots ,0|)$ . We can consider two-sided sequences or e.g. our solenoid $\Lambda $ identifying sequences with the same future, or past as for our $W^s$ values and $f^{-1}$ . Compare Definition 2.1.

In particular, the following holds.

Lemma 7.2. For every Hölder $\phi $ and $\psi $ , for every $\varepsilon>0$ , there exist $C>0$ and $\tau>0$ such that for every $n\in \mathbb {N}$ ,

(7.1) $$ \begin{align} \mu_\varphi\bigg(\bigg\{x\in X: \bigg|S_n \psi(x) - n\int_{\Sigma_d^+}\psi\,d\mu_\phi\bigg|\ge n\varepsilon\bigg\}\bigg)\le C \exp (-n\tau). \end{align} $$

In §§3 and 4, proving e.g. that $\mu _x^s(NL^w\cap W^s_x)=0$ in Lemma 3.6, we did not use large deviations. In §5, we already did (the qualitative version of Lemma 7.2. Now we shall show how the usage of large deviations, Lemma 7.1, allows to estimate from above Hausdorff dimension of the set in each $W^s_x$ where the holonomy is not locally Lipschitz, thus strengthening Lemma 3.6. See also notation in and after Lemma 2.9.

Proposition 7.3. For every $W^s_x$ , the strict inequality $\operatorname {\mathrm {HD}}( NL^w\cap W^s_x) < t_0=\operatorname {\mathrm {HD}}(\Lambda \cap W^s_x)$ holds. More precisely,

(7.2) $$ \begin{align} \operatorname{\mathrm{HD}} (NL^w\cap W^s_x) \le \inf_{\varepsilon>0}\max \{A_\varepsilon, B_\varepsilon\}, \end{align} $$

where

$$ \begin{align*}A_{\varepsilon}= t_0-(I_\varepsilon(\log\unicode{x3bb}',\varepsilon)/\chi_\mu(\unicode{x3bb}'))\bigg/ \bigg(1+\frac{-\chi_\mu(\unicode{x3bb}') - \varepsilon}{\chi_\mu(\eta')-\varepsilon}\bigg) \end{align*} $$

and the same with $\log \unicode{x3bb} '$ replaced by $-\log \eta '$ . Also, with the latter fraction above replaced by its inverse,

$$ \begin{align*}B_{\varepsilon}=t_0 -\frac{t_0 (1-\varepsilon/\chi_\mu(\unicode{x3bb}') - ({\chi_\mu(\eta') + \varepsilon})/({-\chi_\mu(\unicode{x3bb}')-\varepsilon})) (-\chi_\mu(\unicode{x3bb}')) } {(1+({\chi_\mu(\eta') + \varepsilon})/){-\chi_\mu(\unicode{x3bb}')-\varepsilon})) (-\chi_\mu(\unicode{x3bb}')+\varepsilon)}. \end{align*} $$

Here, $A_\varepsilon $ bounds Hausdorff dimension of the irregular part and $B_\varepsilon $ bounds Hausdorff dimension of the regular non-Lipschitz part.

For $\varepsilon \approx 0$ , the number $A_\varepsilon $ is bigger. On the other end, for $({\chi _\mu (\eta ') + \varepsilon })/({-\chi _\mu (\unicode{x3bb} ')-\varepsilon })$ almost 1, the number $B_\varepsilon $ dominates. Optimum is in between.

Proof First we prove the estimate (7.2) for $B_\varepsilon $ . We rely on §5, the proof of Theorem 5.1, Step 1. The coefficient $\alpha $ is not needed, since $NL^w$ is a local property and overlappings of remote cylinders do not count (see the proof of Theorem 5.1, Step 3).

We obtain the uniform estimate for every $(\unicode{x3bb} ,\varepsilon ,m)$ -backward regular $H_m$ , with n satisfying equation (5.3) Its ‘contaminated part’ can be estimated as follows, see equations (5.4) and (4.10),

(7.3)

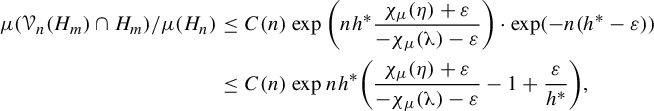
where $C(n)$ grows sub-exponentially. We used here, as already e.g. in equation (5.4), the fact that $\operatorname {\mathrm {Const}}^{-1}\mu (H_m \cap V_n)/ \mu (H_m) \mu (V_n) <\operatorname {\mathrm {Const}}$ following from Gibbs property of $\mu $ .

Now by summing over regular $H_m$ with weights $\mu (H_m)$ , we get the same estimate for and by the f-invariance of $\mu $ , the same estimate for for $n=n(\varepsilon ,m)$ , built of cylinders $H_{m+n}$ .

Now we shall translate the measure estimate above for all $m, n(\varepsilon ,m)$ , to an estimate of Hausdorff dimension.

Denote $\mu (\textbf {H}'(n))$ by $\overline \mu _n$ . By Gibbs property of $\mu =\mu _{t_0}$ and using normalized restrictions $\mu _n:=\mu |_{\textbf {H}'(n)}/\overline \mu _n$ , considering conditional measures on $W^s$ (not changing notation), we get for each $H_{n+m}\subset \textbf {H}'(n)$ and p in it,

(7.4)

where $\vartheta _n:={\log \overline \mu _n}/({(n+m)(\chi _\mu (\unicode{x3bb} ')-\varepsilon )})$ , with m expressed by n maximal possible to satisfy equation (5.3). So, for any $x\in S^1$ ,

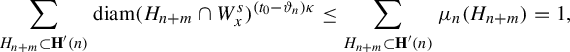(7.5) $$ \begin{align} \sum_{H_{n+m}\subset\textbf{H}'(n)} \operatorname{\mathrm{diam}} (H_{n+m} \cap W^s_x)^{(t_0-\vartheta_n)\kappa} \le \sum_{H_{n+m}\subset\textbf{H}'(n)} \mu_n (H_{n+m})=1, \end{align} $$

where $\kappa =({\chi _\mu (\unicode{x3bb} ') -e})/{\chi _\mu (\unicode{x3bb} ')}$ . By an arbitrarily small change of $\kappa $ , we can assure the bound by 1 replaced by numbers tending exponentially to 0 as $m\to \infty $ , allowing summing over m.

So, taking $\varepsilon \to 0$ , for $\vartheta :=\liminf _{n\to \infty }\vartheta _n$ ,

$$ \begin{align*}\operatorname{\mathrm{HD}}(NL^w\cap W^s_x) \le \operatorname{\mathrm{HD}}\Big(\limsup_{n\to\infty} \textbf{H}'(n)\Big) \le \vartheta. \end{align*} $$

This, after simple calculations, yields the estimate by $B_\varepsilon $ in our Proposition. For an explanation of the structure of $L^s$ complementary to the set $NL^w \subset \limsup _{n\to \infty } \textbf {H}'(n)$ , (with $2n$ there in place of $m+n$ here), see Remark 5.3.

Now we estimate the irregular (backward) part, related to $A_\varepsilon $ . For this, we define similarly to $\textbf {H}_i$ in §5 but with $k=0$ and $\alpha =1$ . We add $\unicode{x3bb} ,\eta $ and $\varepsilon $ in the notation of $\textbf {H}_i$ . We consider

$$ \begin{align*}\textbf{H}_1(\unicode{x3bb},\varepsilon,m, \operatorname{\mathrm{irreg}})\subset \bigcup H_{m+n}\end{align*} $$

and

$$ \begin{align*}\textbf{H}_2(\eta,\varepsilon,n, \operatorname{\mathrm{irreg}})\subset \bigcup H_{m+n}.\end{align*} $$

We define also as in the proof of Theorem 5.1, Step 3, the set

$$ \begin{align*}\textbf{H}_3(\xi,\varepsilon, n, \operatorname{\mathrm{irreg}})\subset \bigcup H_{m+n} \quad\text{ for }\xi=\unicode{x3bb},\nu.\end{align*} $$

Applying Lemma 7.1 for $\psi =\log \unicode{x3bb} '$ , replacing m by $n+m$ , we get for $\textbf {H}_1$ ,

$$ \begin{align*}\operatorname{\mathrm{HD}} (\limsup \textbf{H}_1(\unicode{x3bb},\varepsilon,m, \operatorname{\mathrm{irreg}})) \le t_0 - (I(\log\unicode{x3bb}',\varepsilon)/\chi_\mu(\unicode{x3bb}')) \bigg/ \bigg(1+\frac{-\chi_\mu(\unicode{x3bb}')-\varepsilon}{\chi_\mu(\eta') + \varepsilon}\bigg), \end{align*} $$

for $\textbf {H}_2$ , replacing n by $n+m$ ,

$$ \begin{align*}\operatorname{\mathrm{HD}} (\limsup \textbf{H}_2(\eta,\varepsilon,n, \operatorname{\mathrm{irreg}})) \le t_0 - (I(-\log\eta',\varepsilon)/\chi_\mu(\unicode{x3bb}')) \bigg/ \bigg(1+\frac{\chi_\mu(\eta') + \varepsilon}{-\chi_\mu(\unicode{x3bb}')-\varepsilon}\bigg) \end{align*} $$

and for $\textbf {H}_3$ ,

$$ \begin{align*}\kern-10pt\operatorname{\mathrm{HD}} (\limsup \textbf{H}_3(\unicode{x3bb},\varepsilon, n, \operatorname{\mathrm{irreg}})) \le t_0 - (I(\log\unicode{x3bb}',\varepsilon)/\chi_\mu(\unicode{x3bb}')) \bigg/ \bigg(1+\frac{\chi_\mu(\eta') + \varepsilon}{-\chi_\mu(\unicode{x3bb}')-\varepsilon}\bigg).\\[-43pt] \end{align*} $$

7.2 Generalization to one-dimensional expanding attractors

All the theorems in this paper hold also for hyperbolic expanding attractors in dimension 3 with one-dimensional unstable manifolds, non-uniformly thin (see definition in §1) and satisfying the transversality assumption, of which our solenoids are examples. The only exception is the Theorem 6.1 on singularity of Hausdorff measures, where the assumption that for some $p,q\in \Lambda $ , a non-empty intersection of projections $\widehat W^u(p)$ and $\widehat W^u(q)$ is needed. For our solenoids, it holds automatically, but for extensions to $\mathbb {R}^3$ of say Plykin or DA attractor, it is not so. See [18].

Proofs are the same since these attractors are extensions of expanding maps on branched 1-manifolds and Markov coding can be used.

7.3 More on solenoids—coordinates

In fact, Theorems 1.2–1.6 hold for

(7.6) $$ \begin{align} f(x,y,z):= (\eta(x,y,z), \unicode{x3bb}(x,y,z) + u(x), \nu(x,y,z ) + v(x)), \end{align} $$

of class $C^{1+\varepsilon }$ , injective, such that $f(\operatorname {\mathrm {cl}} M)\subset M$ , satisfying $\unicode{x3bb} (x,0,0)=\nu (x,0,0)=0$ , with hyperbolic attractor $\Lambda $ , and satisfying transversality, the non-conformal form more general than f in the triangular in equation (1.1).

Indeed, we are interested in a non-conformal solenoid, so we assume that the tangent bundle on M, or at least on $\Lambda $ , splits into $T_\Lambda M=E^u \oplus E^{s}$ , $Df$ invariant, where $E^s$ , the stable one, splits further into weak stable and strong stable $T_\Lambda M= E^u \oplus E^{ws} \oplus E^{ss}$ , or at least $E^s$ contains a strong stable $E^{ss}$ . Note that $E^s$ is dynamically defined on the whole M, not only on $\Lambda $ , by $E^s(p):=\lim Df^{-n} (C^s(f^n(p)))$ , where $C^s$ denotes a stable cone taken equal to a cone at a point in $\Lambda $ near $f^n(p)$ . Similarly, one proves that the bundle $E^s$ on M is integrable to a stable foliation of M. As having codimension one, it is $C^{1+\varepsilon }$ , see [11]. Therefore, under an appropriate $C^{1+\varepsilon }$ change of coordinates, it becomes the foliation of M by vertical discs $W^s_x=\{x\}\times \mathbb {D}$ .

Additionally, strong stable foliation (of the whole M as obtained as a limit from the future) can be made consisting of vertical intervals, that is, with $x,y$ constant. This foliation is known to be $C^{1+\varepsilon }$ in , see [5], so, after a change of coordinates so that it becomes vertical, our diffeomorphism is $C^{1+\varepsilon }$ in each $W^s$ . However, we do not know what is the smoothness of f in the new coordinates in the whole M.

Therefore, to deduce this general case from our triangular case by change of coordinates, we just assume is $C^{1+\varepsilon }$ in M. A question stays open whether this assumption is needed, that is, whether we really use f being $C^{1+\varepsilon }$ in the triangular coordinates.

The following completes the topological picture. Suppose f is already in the triangular form.

Lemma 7.4. There exists on M a change of coordinates $\Psi (x,y,z)=(x,y,\psi (y,z)$ , bi-Lipschitz continuous, such that the foliation into the sets $x,z$ constant is invariant and its $\Psi ^{-1}$ -image is a central stable foliation with leaves $C^1$ smooth.

Proof Extend f to $\tilde f :S^1 \times \mathbb {R}^2\to S^1 \times \mathbb {R}^2$ so that $\unicode{x3bb} $ and $\nu $ are linear with respect to y and z, respectively, far from M.

Next find as a limit of , where is the foliation of M into the intervals $x,z$ constant. By bounded distortion, one gets Lipschitz property of the limit and, in particular, a true foliation (leaves do no glue partially to each other in the limit).

Our $Df$ in these coordinates would be diagonal which would ease estimates. Unfortunately, this central stable foliation and, therefore, f in the new coordinates seems usually not $C^{1+\varepsilon }$ .

7.4 Summary of our strategies

The key objects in the paper are ‘rectangles’ being intersection of horizontal and vertical strips $\widehat H_m$ and $\widehat V_n$ , ‘cylinders’ of level m and n, projections to the plane $(x,y)$ of tubes and thickened discs. Such Markov rectangles are basic objects in hyperbolic dynamics.

Horizontal strips can intersect transversally other horizontal strips. An issue is to estimate how the large part of any horizontal strip is intersected, ‘contaminated’ by other horizontal strips, measured in a number of contaminated (with margins) rectangles. The tool is going backward by $f^{-m}$ or forward by $f^n$ to large scale, so that the rectangles become full (that is, over $[0,2\pi ]$ ) horizontal strips and results do not depend on sections by stable discs $W^s$ . We distinguish Birkhoff irregular sets among full unstable manifolds (over $[0,2\pi ]$ ) and prove they have stable SRB-measure 0 and even Hausdorff dimension in each $W^s$ less than the dimension of $\Lambda \cap W^s$ . We estimate also the size of the contaminated set of Birkhoff regular unstable manifolds. In each section, the choice of m to n (or vice versa) and auxiliary k is different, depending on our needs.