1 results
LINEAR QUOTIENTS AND MULTIGRADED SHIFTS OF BOREL IDEALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 30 January 2019, pp. 48-57
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
-
We investigate whether the property of having linear quotients is inherited by ideals generated by multigraded shifts of a Borel ideal and a squarefree Borel ideal. We show that the ideal generated by the first multigraded shifts of a Borel ideal has linear quotients, as do the ideal generated by the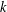
$k$th multigraded shifts of a principal Borel ideal and an equigenerated squarefree Borel ideal for each 
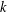$k$. Furthermore, we show that equigenerated squarefree Borel ideals share the property of being squarefree Borel with the ideals generated by multigraded shifts.
