Published online by Cambridge University Press: 30 January 2019
We investigate whether the property of having linear quotients is inherited by ideals generated by multigraded shifts of a Borel ideal and a squarefree Borel ideal. We show that the ideal generated by the first multigraded shifts of a Borel ideal has linear quotients, as do the ideal generated by the 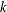 $k$th multigraded shifts of a principal Borel ideal and an equigenerated squarefree Borel ideal for each
$k$th multigraded shifts of a principal Borel ideal and an equigenerated squarefree Borel ideal for each 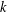 $k$. Furthermore, we show that equigenerated squarefree Borel ideals share the property of being squarefree Borel with the ideals generated by multigraded shifts.
$k$. Furthermore, we show that equigenerated squarefree Borel ideals share the property of being squarefree Borel with the ideals generated by multigraded shifts.