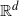1 results
Topological reconstruction of compact supports of dependent stationary random variables
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 02 April 2024, pp. 1339-1369
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
-
In this paper we extend results on reconstruction of probabilistic supports of independent and identically distributed random variables to supports of dependent stationary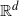
${\mathbb R}^d$-valued random variables. All supports are assumed to be compact of positive reach in Euclidean space. Our main results involve the study of the convergence in the Hausdorff sense of a cloud of stationary dependent random vectors to their common support. A novel topological reconstruction result is stated, and a number of illustrative examples are presented. The example of the Möbius Markov chain on the circle is treated at the end with simulations.
