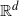1. Introduction
Given a sequence of stationary random variables of unknown common law and unknown compact support
![]() $\mathrm{I\!M}$
(Section 3), it can be very useful in practice to identify topological properties of
$\mathrm{I\!M}$
(Section 3), it can be very useful in practice to identify topological properties of
![]() $\mathrm{I\!M}$
based on observed data. Data analysis in high-dimensional spaces from a probabilistic point of view was initiated in [Reference Niyogi, Smale and Weinberger33], where data was assumed to be drawn from sampling an independent and identically distributed (i.i.d.) probability distribution on (or near) a submanifold
$\mathrm{I\!M}$
based on observed data. Data analysis in high-dimensional spaces from a probabilistic point of view was initiated in [Reference Niyogi, Smale and Weinberger33], where data was assumed to be drawn from sampling an independent and identically distributed (i.i.d.) probability distribution on (or near) a submanifold
![]() $\mathrm{I\!M}$
of Euclidean space. Topological properties of
$\mathrm{I\!M}$
of Euclidean space. Topological properties of
![]() $\mathrm{I\!M}$
(homotopy type and homology) were deduced based on the random samples and the geometrical properties of
$\mathrm{I\!M}$
(homotopy type and homology) were deduced based on the random samples and the geometrical properties of
![]() $\mathrm{I\!M}$
. Several papers on probability and topological inference ensued, some taking a persistence homology approach by providing a confidence set for persistence diagrams corresponding to the Hausdorff distance of a sample from a distribution supported on
$\mathrm{I\!M}$
. Several papers on probability and topological inference ensued, some taking a persistence homology approach by providing a confidence set for persistence diagrams corresponding to the Hausdorff distance of a sample from a distribution supported on
![]() $\mathrm{I\!M}$
[Reference Fasy16].
$\mathrm{I\!M}$
[Reference Fasy16].
Topology intervenes in probability through reconstruction results (see [Reference Attali, Lieutier and Salinas3, Reference Chazal, Glisse, Labruyère and Michel7, Reference Chazal and Oudot8, Reference Fasy16, Reference Kim29, Reference Niyogi, Smale and Weinberger33] and references therein). This research direction is now recognized as part of ‘manifold learning’. Given an n-point cloud
![]() ${\mathbb X}_n$
lying in a support
${\mathbb X}_n$
lying in a support
![]() $\mathrm{I\!M}$
, which is generally assumed to be a compact subspace of
$\mathrm{I\!M}$
, which is generally assumed to be a compact subspace of
![]() ${\mathbb R}^d$
for some
${\mathbb R}^d$
for some
![]() $d>0$
, and given a certain probability distribution of these n points on
$d>0$
, and given a certain probability distribution of these n points on
![]() $\mathrm{I\!M}$
, one can formulate from this data practical conditions to reconstruct, up to homotopy or up to homology, the support
$\mathrm{I\!M}$
, one can formulate from this data practical conditions to reconstruct, up to homotopy or up to homology, the support
![]() $\mathrm{I\!M}$
. Reconstruction up to homotopy means recovering the homotopy type of
$\mathrm{I\!M}$
. Reconstruction up to homotopy means recovering the homotopy type of
![]() $\mathrm{I\!M}$
. Reconstruction up to homology means determining, up to a certain degree, the homology groups of
$\mathrm{I\!M}$
. Reconstruction up to homology means determining, up to a certain degree, the homology groups of
![]() $\mathrm{I\!M}$
. Recovering the geometry of
$\mathrm{I\!M}$
. Recovering the geometry of
![]() $\mathrm{I\!M}$
, including curvature and volume, is a much more delicate task (see [Reference Aamari and Levrard1, Reference Divol13, Reference Fefferman, Mitter and Narayanan18, Reference Niyogi, Smale and Weinberger33, Reference Wang and Wang39]).
$\mathrm{I\!M}$
, including curvature and volume, is a much more delicate task (see [Reference Aamari and Levrard1, Reference Divol13, Reference Fefferman, Mitter and Narayanan18, Reference Niyogi, Smale and Weinberger33, Reference Wang and Wang39]).
The goal of our work is to extend work of Nigoyi, Smale and Weinberger [Reference Niyogi, Smale and Weinberger33] from data drawn from sampling an i.i.d. probability distribution that has support on a smooth submanifold
![]() $\mathrm{I\!M}$
of Euclidean space to data drawn from stationary dependent random variables concentrated inside a compact space of positive reach (or PR set). It is fitting here to define this notion: the reach of a closed set S in a metric space is the supremum
$\mathrm{I\!M}$
of Euclidean space to data drawn from stationary dependent random variables concentrated inside a compact space of positive reach (or PR set). It is fitting here to define this notion: the reach of a closed set S in a metric space is the supremum
![]() $\tau\geq 0$
such that any point within distance less than
$\tau\geq 0$
such that any point within distance less than
![]() $\tau$
of S has a unique nearest point in S. Spaces of positive reach
$\tau$
of S has a unique nearest point in S. Spaces of positive reach
![]() $\tau$
were introduced in [Reference Federer17]; they form a natural family of spaces that are more general than convex sets
$\tau$
were introduced in [Reference Federer17]; they form a natural family of spaces that are more general than convex sets
![]() $(\tau=\infty$
) or smooth submanifolds, but share many of their common integro-geometric properties, such as ‘curvature measures’ [Reference Thale38] (see Section 2).
$(\tau=\infty$
) or smooth submanifolds, but share many of their common integro-geometric properties, such as ‘curvature measures’ [Reference Thale38] (see Section 2).
The interest in going beyond independence lies in the fact that many observations in everyday life are dependent, and independence is not sufficient to describe these phenomena. The study of the data support topologically and geometrically in this case can be instrumental in directional statistics, for example, where the observations are often correlated. This can provide information on animal migration paths or wind directions, for instance. Modeling by a Markov chain on an unknown compact manifold, with or without boundary, makes it possible to study such examples. Other illustrative examples can be found in more applied fields, for instance in cosmology [Reference Cisewski-Kehe9], medicine [Reference Iniesta20], imaging [Reference Singh37], biology [Reference Amézquita2], and environmental science [Reference Hoef, Adams, King and Ebert-Uphoff22].
To get information on an unknown support from stationary dependent data, we need to study the convergence in the Hausdorff distance
![]() $d_H$
of the data, seen as a (finite) point cloud, to its support, similarly to what was done in the i.i.d. case [Reference Chazal, Glisse, Labruyère and Michel7, Reference Cuevas10, Reference Cuevas and Rodrguez-Casal11, Reference Fasy16]. The main feature of interest in the metric
$d_H$
of the data, seen as a (finite) point cloud, to its support, similarly to what was done in the i.i.d. case [Reference Chazal, Glisse, Labruyère and Michel7, Reference Cuevas10, Reference Cuevas and Rodrguez-Casal11, Reference Fasy16]. The main feature of interest in the metric
![]() $d_H$
is the following property: if
$d_H$
is the following property: if
![]() $S\subset M$
is this point cloud in M, then
$S\subset M$
is this point cloud in M, then
![]() $d_H(S,M)\leq \epsilon$
is equivalent to S being
$d_H(S,M)\leq \epsilon$
is equivalent to S being
![]() $\epsilon$
-dense in M (see Section 2). We can expand this relationship to the random case as follows.
$\epsilon$
-dense in M (see Section 2). We can expand this relationship to the random case as follows.
Definition 1.1. We say that a point cloud
![]() ${\mathbb X}_n$
of n stationary dependent
${\mathbb X}_n$
of n stationary dependent
![]() ${\mathbb R}^d$
-valued random variables is
${\mathbb R}^d$
-valued random variables is
![]() $(\epsilon,\alpha)$
-dense in
$(\epsilon,\alpha)$
-dense in
![]() $\mathrm{I\!M}\subset{\mathbb R}^d$
, for given
$\mathrm{I\!M}\subset{\mathbb R}^d$
, for given
![]() $\epsilon> 0$
and
$\epsilon> 0$
and
![]() $\alpha\in ]0,1[$
, if
$\alpha\in ]0,1[$
, if
If
![]() , with
, with
![]() being
being
![]() ${\mathbb Z}$
,
${\mathbb Z}$
,
![]() $\mathrm{I\!N}$
, or
$\mathrm{I\!N}$
, or
![]() $\mathrm{I\!N}\setminus \{0\}$
, is a stationary sequence of
$\mathrm{I\!N}\setminus \{0\}$
, is a stationary sequence of
![]() $\mathrm{I\!R}^d$
-valued random variables, we say that
$\mathrm{I\!R}^d$
-valued random variables, we say that
![]() ${\mathbb X}$
is asymptotically dense in
${\mathbb X}$
is asymptotically dense in
![]() $\mathrm{I\!M}\subset{\mathbb R}^d$
if, for all positive
$\mathrm{I\!M}\subset{\mathbb R}^d$
if, for all positive
![]() $\epsilon$
sufficiently small and any
$\epsilon$
sufficiently small and any
![]() $0<\alpha <1$
, there exists a positive integer
$0<\alpha <1$
, there exists a positive integer
![]() $n_0(\epsilon,\alpha)$
such that for every
$n_0(\epsilon,\alpha)$
such that for every
![]() $n\geq n_0(\epsilon,\alpha)$
,
$n\geq n_0(\epsilon,\alpha)$
,
![]() ${\mathbb X}_n=\{X_1,\ldots, X_n\}$
is
${\mathbb X}_n=\{X_1,\ldots, X_n\}$
is
![]() $(\epsilon,\alpha)$
-dense in
$(\epsilon,\alpha)$
-dense in
![]() $\mathrm{I\!M}$
.
$\mathrm{I\!M}$
.
The first undertaking of this paper is to identify sequences of dependent random vectors which are asymptotically dense in a compact support. In Sections 4 and 5 we treat explicitly a number of examples and show for all of these that the property of being asymptotically dense in the compact support holds by means of a key technical result, Proposition 3.1, which uses blocking techniques to give upper bounds for
![]() $\mathrm{I\!P}\!\left(d_H({\mathbb X}_n , {\mathrm{I\!M}}) > \epsilon\right)$
. Blocking techniques are very useful in the theory of limit theorems for stationary dependent random variables, and the underlying idea is to view and manipulate blocks as ‘independent’ clusters of dependent variables.
$\mathrm{I\!P}\!\left(d_H({\mathbb X}_n , {\mathrm{I\!M}}) > \epsilon\right)$
. Blocking techniques are very useful in the theory of limit theorems for stationary dependent random variables, and the underlying idea is to view and manipulate blocks as ‘independent’ clusters of dependent variables.
We summarize our first set of results into one main theorem. Given
![]() a stationary sequence of
a stationary sequence of
![]() $\mathrm{I\!R}^d$
-valued random variables, we denote by
$\mathrm{I\!R}^d$
-valued random variables, we denote by
![]() $\rho_m(\epsilon)$
the concentration quantity of the block
$\rho_m(\epsilon)$
the concentration quantity of the block
![]() $(X_1,\ldots, X_m)$
; that is, for
$(X_1,\ldots, X_m)$
; that is, for
![]() $\epsilon>0$
,
$\epsilon>0$
,
where
![]() $\mathrm{I\!M}_{dm}$
denotes the support of the vector transpose
$\mathrm{I\!M}_{dm}$
denotes the support of the vector transpose
![]() $(X_1,\cdots,X_{m})^t$
.
$(X_1,\cdots,X_{m})^t$
.
Theorem 1.1. The following stationary sequences of
![]() $\mathrm{I\!R}^d$
-valued random variables are asymptotically dense in their common compact support:
$\mathrm{I\!R}^d$
-valued random variables are asymptotically dense in their common compact support:
-
1. Stationary m-dependent sequences such that for any
 $\epsilon>0$
, there exists a strictly positive constant
$\epsilon>0$
, there exists a strictly positive constant
 $\kappa_{\epsilon}$
such that
$\kappa_{\epsilon}$
such that
 $\displaystyle\rho_{m+1}(\epsilon) \geq \kappa_{\epsilon}.$
(See Proposition 4.1.)
$\displaystyle\rho_{m+1}(\epsilon) \geq \kappa_{\epsilon}.$
(See Proposition 4.1.) -
2. Stationary m-approximable random variables on a compact set. These are stationary models that can be approximated by m-dependent stationary sequences (see Paragraph 4.0.2 and Proposition 4.2).
-
3. Stationary
 $\beta$
-mixing sequences, with
$\beta$
-mixing sequences, with
 $(\beta_n)_n$
coefficients (see (4.6) for their definition), such that for some
$(\beta_n)_n$
coefficients (see (4.6) for their definition), such that for some
 $\beta>1$
, and any
$\beta>1$
, and any
 $\epsilon>0$
, (See Proposition 4.3.)
$\epsilon>0$
, (See Proposition 4.3.) \begin{align*}\lim_{m\rightarrow \infty} \rho_m(\epsilon)\frac{e^{m^{\beta}}}{m^{1+\beta}}=\infty,\,\,\,{{\textit{and}}}\,\,\,\lim_{m\rightarrow\infty} \frac{e^{2m^{\beta}}}{m^2}\beta_m=0.\end{align*}
\begin{align*}\lim_{m\rightarrow \infty} \rho_m(\epsilon)\frac{e^{m^{\beta}}}{m^{1+\beta}}=\infty,\,\,\,{{\textit{and}}}\,\,\,\lim_{m\rightarrow\infty} \frac{e^{2m^{\beta}}}{m^2}\beta_m=0.\end{align*}
-
4. Stationary weakly dependent sequences, with
 $(\Psi(n))_n$
dependent coefficients (as introduced in (4.7)), such that for some
$(\Psi(n))_n$
dependent coefficients (as introduced in (4.7)), such that for some
 $\beta>1$
and any
$\beta>1$
and any
 $\epsilon>0$
, (See Proposition 4.4.)
$\epsilon>0$
, (See Proposition 4.4.) \begin{align*}\lim_{m\rightarrow \infty} \rho_m(\epsilon)\frac{e^{m^{\beta}}}{m^{1+\beta}}=\infty,\,\,\,{{\textit{and}}}\,\,\,\lim_{m\rightarrow\infty} \frac{e^{2m^{\beta}}}{m^2}\Psi(m)=0.\end{align*}
\begin{align*}\lim_{m\rightarrow \infty} \rho_m(\epsilon)\frac{e^{m^{\beta}}}{m^{1+\beta}}=\infty,\,\,\,{{\textit{and}}}\,\,\,\lim_{m\rightarrow\infty} \frac{e^{2m^{\beta}}}{m^2}\Psi(m)=0.\end{align*}
-
5. Stationary Markov chains with an invariant measure
 $\mu$
and a suitable transition probability kernel (see Assumptions (
$\mu$
and a suitable transition probability kernel (see Assumptions (
 ${\mathcal A}_1)$
and (
${\mathcal A}_1)$
and (
 ${\mathcal A}_2)$
of Section 5). (See Propositions 5.1 and 5.2.)
${\mathcal A}_2)$
of Section 5). (See Propositions 5.1 and 5.2.)
Furthermore, and for each sequence
![]() ${\mathbb X}$
of random variables listed in Theorem 1.1, we give methods for finding a threshold
${\mathbb X}$
of random variables listed in Theorem 1.1, we give methods for finding a threshold
![]() $n_0(\epsilon,\alpha)$
, sometimes with explicit formulae for it, such that
$n_0(\epsilon,\alpha)$
, sometimes with explicit formulae for it, such that
![]() ${\mathbb X}_n$
is
${\mathbb X}_n$
is
![]() $(\epsilon,\alpha)$
-dense in the common support for
$(\epsilon,\alpha)$
-dense in the common support for
![]() $n\geq n_0(\epsilon,\alpha)$
.
$n\geq n_0(\epsilon,\alpha)$
.
The next step is topological and consists in showing that when the Hausdorff distance between
![]() ${\mathbb X}_n$
and the support is sufficiently small, it is possible to reconstruct the support up to homotopy. We denote by B(x, r) the closed ball in the Euclidean metric centered at x with radius
${\mathbb X}_n$
and the support is sufficiently small, it is possible to reconstruct the support up to homotopy. We denote by B(x, r) the closed ball in the Euclidean metric centered at x with radius
![]() $r>0$
, and we write
$r>0$
, and we write
![]() ${Y\overset{\simeq}{\longrightarrow}X}$
to mean that X deformation retracts onto Y with
${Y\overset{\simeq}{\longrightarrow}X}$
to mean that X deformation retracts onto Y with
![]() $Y\subset X$
(more precisely, this means that the identity map of X is homotopic to a retraction onto Y, leaving Y fixed during the homotopy).
$Y\subset X$
(more precisely, this means that the identity map of X is homotopic to a retraction onto Y, leaving Y fixed during the homotopy).
Theorem 1.2. Let
![]() be a stationary sequence of
be a stationary sequence of
![]() $\mathrm{I\!R}^d$
-valued random variables with compact support
$\mathrm{I\!R}^d$
-valued random variables with compact support
![]() $\mathrm{I\!M}$
having positive reach
$\mathrm{I\!M}$
having positive reach
![]() $\tau$
. Let
$\tau$
. Let
![]() $\epsilon\in \left(0, \frac{\tau}{2}\right)$
,
$\epsilon\in \left(0, \frac{\tau}{2}\right)$
,
![]() $r\in \left(\epsilon, \frac{\tau}{2}\right)$
and suppose that
$r\in \left(\epsilon, \frac{\tau}{2}\right)$
and suppose that
![]() ${\mathbb X}_n$
is
${\mathbb X}_n$
is
![]() $(\frac{\epsilon}{2},\alpha)$
-dense in
$(\frac{\epsilon}{2},\alpha)$
-dense in
![]() $\mathrm{I\!M}$
. Then
$\mathrm{I\!M}$
. Then
 \begin{align*}\mathrm{I\!P}\!\left(\displaystyle{\mathrm{I\!M}\overset{\simeq}{\longrightarrow}\bigcup_{x\in{\mathbb X}_n}B(x,r)}\right) \geq 1-\alpha.\end{align*}
\begin{align*}\mathrm{I\!P}\!\left(\displaystyle{\mathrm{I\!M}\overset{\simeq}{\longrightarrow}\bigcup_{x\in{\mathbb X}_n}B(x,r)}\right) \geq 1-\alpha.\end{align*}
The proof of this theorem is an immediate consequence of Definition 1.1 and a key reconstruction result proven in Section 2 (Theorem 2.2) which gives the same minimal conditions for recovering the homotopy type of the support
![]() $\mathrm{I\!M}$
from a sample of points
$\mathrm{I\!M}$
from a sample of points
![]() ${\mathbb X}_n$
in
${\mathbb X}_n$
in
![]() $\mathrm{I\!M}$
. Theorem 2.2 is ‘deterministic’ and should have wider application. The key geometric ideas behind this result are in [Reference Niyogi, Smale and Weinberger33], and in its extension in [Reference Wang and Wang39], as applied to the approximation of Riemannian submanifolds. To get Theorem 1.2, we weaken the regularity condition on the submanifolds from smooth to
$\mathrm{I\!M}$
. Theorem 2.2 is ‘deterministic’ and should have wider application. The key geometric ideas behind this result are in [Reference Niyogi, Smale and Weinberger33], and in its extension in [Reference Wang and Wang39], as applied to the approximation of Riemannian submanifolds. To get Theorem 1.2, we weaken the regularity condition on the submanifolds from smooth to
![]() $C^{1,1}$
, and in the hypersurface case we strengthen the bounds on the reach. This is then applied to thickenings of a positive-reach set M (see Section 2). It is important to contrast this result with earlier results in [Reference Kim29] (especially [Reference Kim29, Theorem 19]). There, the radii of the balls can be different. However, our Theorem 1.2 is simpler to state and easier to apply.
$C^{1,1}$
, and in the hypersurface case we strengthen the bounds on the reach. This is then applied to thickenings of a positive-reach set M (see Section 2). It is important to contrast this result with earlier results in [Reference Kim29] (especially [Reference Kim29, Theorem 19]). There, the radii of the balls can be different. However, our Theorem 1.2 is simpler to state and easier to apply.
Having stated our main results, which are mainly of probabilistic and topological interest, we can say a few words about the statistical implications. In practice, the point-cloud data are realizations of random variables living in unknown support
![]() $\mathrm{I\!M}\subset{\mathbb R}^d$
. We then ask whether this support is a circle, a sphere, a torus, or a more complicated object. If we take sufficiently many points
$\mathrm{I\!M}\subset{\mathbb R}^d$
. We then ask whether this support is a circle, a sphere, a torus, or a more complicated object. If we take sufficiently many points
![]() ${\mathbb X}_n$
, our results tell us that the homology of
${\mathbb X}_n$
, our results tell us that the homology of
![]() $\mathrm{I\!M}$
is the same as the homology of the union of balls around the data
$\mathrm{I\!M}$
is the same as the homology of the union of balls around the data
![]() $\bigcup_{x\in{\mathbb X}_n} B(x,r)$
, and this can be computed in general. The uniform radius r depends on
$\bigcup_{x\in{\mathbb X}_n} B(x,r)$
, and this can be computed in general. The uniform radius r depends on
![]() $\mathrm{I\!M}$
only through its reach, which is then the only quantity we need to estimate or to know a priori. Knowing the homology rules out many geometries for
$\mathrm{I\!M}$
only through its reach, which is then the only quantity we need to estimate or to know a priori. Knowing the homology rules out many geometries for
![]() $\mathrm{I\!M}$
. Note that one may want to find ways to distinguish between a support that is a circle and one that is an annulus. However, conclusions of this sort are beyond the techniques of this paper.
$\mathrm{I\!M}$
. Note that one may want to find ways to distinguish between a support that is a circle and one that is an annulus. However, conclusions of this sort are beyond the techniques of this paper.
1.1. Contents
We now give some more details about the content of the paper and how it is organized. We start by establishing, in Section 2, our result on homotopy reconstruction of a support from a point cloud in the deterministic case. Everything afterward is of probabilistic nature, with point clouds drawn from stationary random variables. In Sections 3 and 4 we state sufficient conditions for obtaining the asymptotically dense property, that is, conditions on concentrations and dependence coefficients under which
![]() $d_H({\mathbb X}_n , {\mathrm{I\!M}}) \leq \epsilon$
with large probability and for n large enough. More precisely, in Section 3 we give general upper bounds for
$d_H({\mathbb X}_n , {\mathrm{I\!M}}) \leq \epsilon$
with large probability and for n large enough. More precisely, in Section 3 we give general upper bounds for
![]() $d_H({\mathbb X}_n,\mathrm{I\!M})$
using blocking techniques, i.e. by grouping the point cloud
$d_H({\mathbb X}_n,\mathrm{I\!M})$
using blocking techniques, i.e. by grouping the point cloud
![]() ${\mathbb X}_n$
into
${\mathbb X}_n$
into
![]() $k_n$
blocks, each block with
$k_n$
blocks, each block with
![]() $r_n$
points being considered as a single point in the appropriate Euclidean space of higher dimension. This is stated in Proposition 3.1, which is the key result of this paper, where the control of
$r_n$
points being considered as a single point in the appropriate Euclidean space of higher dimension. This is stated in Proposition 3.1, which is the key result of this paper, where the control of
![]() $d_H({\mathbb X}_n , {\mathrm{I\!M}})$
is reduced to the behavior of lower bounds of the concentration quantity of one block,
$d_H({\mathbb X}_n , {\mathrm{I\!M}})$
is reduced to the behavior of lower bounds of the concentration quantity of one block,
and of
where, as before,
![]() $\mathrm{I\!M}_{d{r_n}}$
is the support of the block
$\mathrm{I\!M}_{d{r_n}}$
is the support of the block
![]() $(X_1,\cdots,X_{r_n})^t$
. Clearly, for independent random variables, a lower bound for (1.1) is directly connected to a lower bound for (1.2), but this is not the case for dependent random variables, and we need to control (1.1) and (1.2) separately. Section 4 gives our main examples of stationary sequences of
$(X_1,\cdots,X_{r_n})^t$
. Clearly, for independent random variables, a lower bound for (1.1) is directly connected to a lower bound for (1.2), but this is not the case for dependent random variables, and we need to control (1.1) and (1.2) separately. Section 4 gives our main examples of stationary sequences of
![]() ${\mathbb R}^d$
-valued random variables having good convergence properties, under the Hausdorff metric, to the support. For each example we check that conditions needed for the control of (1.1) and (1.2) can be reduced to conditions on the concentration quantity
${\mathbb R}^d$
-valued random variables having good convergence properties, under the Hausdorff metric, to the support. For each example we check that conditions needed for the control of (1.1) and (1.2) can be reduced to conditions on the concentration quantity
![]() $\rho_m(\epsilon)$
associated to the vector
$\rho_m(\epsilon)$
associated to the vector
![]() $(X_1,\cdots,X_m)^t$
, for some fixed number of components
$(X_1,\cdots,X_m)^t$
, for some fixed number of components
![]() $m\in \mathrm{I\!N}\setminus\{0\}$
. In particular, for mixing sequences, the control of
$m\in \mathrm{I\!N}\setminus\{0\}$
. In particular, for mixing sequences, the control of
![]() $d_H({\mathbb X}_n,\mathrm{I\!M})$
is based on assumptions on the behavior of some lower bounds for this concentration quantity
$d_H({\mathbb X}_n,\mathrm{I\!M})$
is based on assumptions on the behavior of some lower bounds for this concentration quantity
![]() $\rho_m(\epsilon)$
in connection with the decay of the mixing dependence coefficients, as illustrated in Theorem 1.1. These lower bounds can be obtained by means of a condition similar to the so-called (a, b)-standard assumption (see for instance [Reference Chazal, Glisse, Labruyère and Michel7, Reference Cuevas10, Reference Cuevas and Rodrguez-Casal11]) used in the case of i.i.d. sequences (i.e. when
$\rho_m(\epsilon)$
in connection with the decay of the mixing dependence coefficients, as illustrated in Theorem 1.1. These lower bounds can be obtained by means of a condition similar to the so-called (a, b)-standard assumption (see for instance [Reference Chazal, Glisse, Labruyère and Michel7, Reference Cuevas10, Reference Cuevas and Rodrguez-Casal11]) used in the case of i.i.d. sequences (i.e. when
![]() $k_n=n$
and
$k_n=n$
and
![]() $r_n=1$
). However, our results in Section 4 generalize the i.i.d. case without assuming the (a, b)-standard assumption (Subsection 4.1).
$r_n=1$
). However, our results in Section 4 generalize the i.i.d. case without assuming the (a, b)-standard assumption (Subsection 4.1).
Section 5 gives explicit illustrations of our main results and techniques in the case of stationary Markov chains. For this model, the quantities in (1.1) and (1.2) can be controlled from the behavior of a positive measure
![]() $\nu$
defining the transition probability kernel of this Markov chain, in particular from the lower bounds of the concentration quantity
$\nu$
defining the transition probability kernel of this Markov chain, in particular from the lower bounds of the concentration quantity
![]() $\nu(B(x,\epsilon)\cap \mathrm{I\!M})$
, for small
$\nu(B(x,\epsilon)\cap \mathrm{I\!M})$
, for small
![]() $\epsilon$
and for
$\epsilon$
and for
![]() $x\in \mathrm{I\!M}$
. The threshold
$x\in \mathrm{I\!M}$
. The threshold
![]() $n_0(\epsilon,\alpha)$
can also be determined explicitly. As a key illustration, in Subsection 5.2 we study the Möbius Markov chain on the circle, where
$n_0(\epsilon,\alpha)$
can also be determined explicitly. As a key illustration, in Subsection 5.2 we study the Möbius Markov chain on the circle, where
![]() $\mathrm{I\!M}$
is the unit circle and
$\mathrm{I\!M}$
is the unit circle and
![]() $\nu$
is the arc length measure on the unit circle. The conditions leading to a suitable control of (1.1) and (1.2) are checked with no further assumptions and the threshold
$\nu$
is the arc length measure on the unit circle. The conditions leading to a suitable control of (1.1) and (1.2) are checked with no further assumptions and the threshold
![]() $n_0(\epsilon,\alpha)$
is computed.
$n_0(\epsilon,\alpha)$
is computed.
Section 6 gives an explicit simulation of a Möbius Markov chain studied in [Reference Kato26]. The intent here is to illustrate both the topological and probabilistic parts in an explicit situation. The simulation outcomes (Figures 4 and 5) are in agreement with the theoretical results thus obtained. Finally, all deferred proofs appear in Section 7.
2. A reconstruction result
Given a point cloud
![]() $S_n=\{x_1,\ldots, x_n\}$
on a metric space M, a standard problem is to reconstruct this space from the given distribution of points as n gets large (see the introduction). Various reconstruction processes in the literature are based on the nerve theorem. This basic but foundational result can be found in introductory books on algebraic topology ([Reference Hatcher23], chapter 4) and in most papers on manifold learning. This section takes a different route.
$S_n=\{x_1,\ldots, x_n\}$
on a metric space M, a standard problem is to reconstruct this space from the given distribution of points as n gets large (see the introduction). Various reconstruction processes in the literature are based on the nerve theorem. This basic but foundational result can be found in introductory books on algebraic topology ([Reference Hatcher23], chapter 4) and in most papers on manifold learning. This section takes a different route.
Below, let us write B(x, r) (resp.
![]() $\mathring{B}(x,r)$
) for the closed (resp. open) ball of radius r, centered at x. Starting with a point cloud
$\mathring{B}(x,r)$
) for the closed (resp. open) ball of radius r, centered at x. Starting with a point cloud
![]() $S_n=\{x_1,\ldots, x_n\}\subset M$
, with M a compact subset of
$S_n=\{x_1,\ldots, x_n\}\subset M$
, with M a compact subset of
![]() ${\mathbb R}^d$
with its Euclidean metric
${\mathbb R}^d$
with its Euclidean metric
![]() $\|\cdot\|$
, we seek conditions on the radius r and on the distribution of the points of
$\|\cdot\|$
, we seek conditions on the radius r and on the distribution of the points of
![]() $S_n$
ensuring that the union of balls
$S_n$
ensuring that the union of balls
![]() $\bigcup_{i=1}^nB(x_i,r)$
deformation retracts onto M. The r-offset (or r-thickening, r-dilation, or r-parallel set, depending on the literature) of a closed set M is defined to be
$\bigcup_{i=1}^nB(x_i,r)$
deformation retracts onto M. The r-offset (or r-thickening, r-dilation, or r-parallel set, depending on the literature) of a closed set M is defined to be
Many of the existing theorems in homotopic and homological inference are about offsets. In terms of those, the Hausdorff distance
![]() $d_H$
between two closed sets A and B is defined to be
$d_H$
between two closed sets A and B is defined to be
(replacing
![]() $\inf$
and
$\inf$
and
![]() $\sup$
with
$\sup$
with
![]() $\min$
and
$\min$
and
![]() $\max$
for compact sets). This is a ‘coarse’ metric in the sense that two closed spaces A and B can be very different topologically and yet be arbitrarily close in Hausdorff distance.
$\max$
for compact sets). This is a ‘coarse’ metric in the sense that two closed spaces A and B can be very different topologically and yet be arbitrarily close in Hausdorff distance.
We say that a subset
![]() $S\subset M$
is
$S\subset M$
is
![]() $\epsilon$
-dense (resp. strictly
$\epsilon$
-dense (resp. strictly
![]() $\epsilon$
-dense) in M, for some
$\epsilon$
-dense) in M, for some
![]() $\epsilon>0$
, if
$\epsilon>0$
, if
![]() $B(p,\epsilon)\cap S \neq\emptyset$
(resp.
$B(p,\epsilon)\cap S \neq\emptyset$
(resp.
![]() $\mathring{B}(p,\epsilon)\cap S \neq\emptyset$
) for each
$\mathring{B}(p,\epsilon)\cap S \neq\emptyset$
) for each
![]() $p\in M$
. We have the following characterization.
$p\in M$
. We have the following characterization.
Lemma 2.1. Let
![]() $S\subset M$
be a closed subset. Then
$S\subset M$
be a closed subset. Then
Proof. When
![]() $S\subset M$
,
$S\subset M$
,
![]() $d_H(S,M) = \inf\{r>0\ | M\subset S^{\oplus r}\}$
. If S is
$d_H(S,M) = \inf\{r>0\ | M\subset S^{\oplus r}\}$
. If S is
![]() $\epsilon$
-dense, any p in M is within
$\epsilon$
-dense, any p in M is within
![]() $\epsilon$
of an
$\epsilon$
of an
![]() $x\in S$
, and so
$x\in S$
, and so
![]() $M\subset S^{\oplus\epsilon}$
, which implies that
$M\subset S^{\oplus\epsilon}$
, which implies that
![]() $d_H(S,M)\leq\epsilon$
. The converse is immediate.
$d_H(S,M)\leq\epsilon$
. The converse is immediate.
From now on, S will always mean a point cloud in M, that is, a finite collection of points. The following is a foundational result in the theory and is our starting point.
Theorem 2.1. ([Proposition 3.1].) Let M be a compact Riemannian submanifold of
![]() ${\mathbb R}^d$
with positive reach
${\mathbb R}^d$
with positive reach
![]() $\tau$
, and
$\tau$
, and
![]() $S \subset M$
a strictly
$S \subset M$
a strictly
![]() $\frac{\epsilon}{2}$
-dense finite subset for
$\frac{\epsilon}{2}$
-dense finite subset for
![]() $\epsilon < \sqrt{\frac{3}{5}}\tau$
. Then for any
$\epsilon < \sqrt{\frac{3}{5}}\tau$
. Then for any
![]() $ r\in [\epsilon , \sqrt{\frac{3}{5}}\tau[$
,
$ r\in [\epsilon , \sqrt{\frac{3}{5}}\tau[$
,
![]() ${M\overset{\simeq}{\longrightarrow}\bigcup_{x\in S }\mathring{B}(x,r)}$
.
${M\overset{\simeq}{\longrightarrow}\bigcup_{x\in S }\mathring{B}(x,r)}$
.
Remark 2.1 Theorem 2.1 is a topological ‘reconstruction’ result which recovers the homotopy type of M from a finite sample. There are many reconstruction methods in the literature, which are too diverse to review here (see [Reference Attali, Lieutier and Salinas3, Reference Divol13, Reference Kim29] and references therein). Reconstructions can be topological, meaning they recover the homotopy type or homology of the underlying manifold M, or they can be geometrical. We address only the topological aspect in this paper. In that regard, [Reference Kim29, Corollary 10] is attractive for its simplicity, as it proves a general reconstruction result for compact sets with positive reach by applying the nerve theorem to a cover by ‘subspace balls’
![]() $\mathcal U_M = \{B(x_i,r)\cap M\}$
. For Riemannian manifolds M, there is an alternative intrinsic geometric method for homotopy reconstruction based on ‘geodesic balls’. Let
$\mathcal U_M = \{B(x_i,r)\cap M\}$
. For Riemannian manifolds M, there is an alternative intrinsic geometric method for homotopy reconstruction based on ‘geodesic balls’. Let
![]() $\rho_c>0$
be a convexity radius for M. Such a radius has the property that around each
$\rho_c>0$
be a convexity radius for M. Such a radius has the property that around each
![]() $p\in M$
, there is a ‘geodesic ball’
$p\in M$
, there is a ‘geodesic ball’
![]() $B_g(p,\rho_c)$
which is convex, meaning that any two points in this neighborhood are joined by a unique geodesic in that neighborhood. These geodesic balls, and their non-empty intersections, are contractible. If
$B_g(p,\rho_c)$
which is convex, meaning that any two points in this neighborhood are joined by a unique geodesic in that neighborhood. These geodesic balls, and their non-empty intersections, are contractible. If
![]() $S_n=\{x_1,\ldots, x_n\}$
is a point cloud such that
$S_n=\{x_1,\ldots, x_n\}$
is a point cloud such that
![]() $ \{B_g(x_i,\rho_c)\}$
is a cover of M, then the associated Čech complex is homotopy equivalent to M by the nerve theorem.
$ \{B_g(x_i,\rho_c)\}$
is a cover of M, then the associated Čech complex is homotopy equivalent to M by the nerve theorem.
2.1. Positive reach
The notion of positive reach is foundational in convex geometry. As indicated in the introduction, the reach of a subset M is defined to be
A PR set is any set M with
![]() $\tau (M)> 0$
. Compact submanifolds are PR. Figure 1 gives an example of a PR set that is not a submanifold. The quintessential property of PR sets is the existence, for
$\tau (M)> 0$
. Compact submanifolds are PR. Figure 1 gives an example of a PR set that is not a submanifold. The quintessential property of PR sets is the existence, for
![]() $0<r<\tau$
, of the ‘unique closest point’ projection
$0<r<\tau$
, of the ‘unique closest point’ projection
with
![]() $\pi_M(y)$
the unique nearest point to y in M. PR sets are necessarily closed, and thus compact if bounded.
$\pi_M(y)$
the unique nearest point to y in M. PR sets are necessarily closed, and thus compact if bounded.

Figure 1. This space has positive reach
![]() $\tau$
in
$\tau$
in
![]() ${\mathbb R}^2$
, but a neighborhood of point A indicates it is not a submanifold (with boundary).
${\mathbb R}^2$
, but a neighborhood of point A indicates it is not a submanifold (with boundary).
As already indicated, we use the notation
![]() ${Y\overset{\simeq}{\longrightarrow}X}$
, if
${Y\overset{\simeq}{\longrightarrow}X}$
, if
![]() $Y\subset X$
, to denote the fact that X deformation retracts onto Y. ‘Thin-enough’ offsets of PR sets deformation retract onto M.
$Y\subset X$
, to denote the fact that X deformation retracts onto Y. ‘Thin-enough’ offsets of PR sets deformation retract onto M.
Lemma 2.2. Let M be a PR set with
![]() $\tau=\tau (M)>0$
. Then
$\tau=\tau (M)>0$
. Then
![]() ${M\overset{\simeq}{\longrightarrow}M^{\oplus r}}$
whenever
${M\overset{\simeq}{\longrightarrow}M^{\oplus r}}$
whenever
![]() $r<\tau$
.
$r<\tau$
.
Proof. This is immediate once we see that if
![]() $p\in M$
and
$p\in M$
and
![]() $x\in \pi^{-1}_M(p)\subset M^{\oplus r}$
, then the entire segment [x, p] of
$x\in \pi^{-1}_M(p)\subset M^{\oplus r}$
, then the entire segment [x, p] of
![]() ${\mathbb R}^d$
must be in
${\mathbb R}^d$
must be in
![]() $\pi_M^{-1}(p)$
, so we can use the homotopy
$\pi_M^{-1}(p)$
, so we can use the homotopy
![]() $F\;:\; M^{\oplus r}\times [0,1]\rightarrow M^{\oplus r}$
,
$F\;:\; M^{\oplus r}\times [0,1]\rightarrow M^{\oplus r}$
,
![]() $F(x,t)=(1-t)x+t\pi_M(x)$
,
$F(x,t)=(1-t)x+t\pi_M(x)$
,
![]() $t\in [0,1]$
, to get a (linear) deformation retraction, with M being fixed during the homotopy.
$t\in [0,1]$
, to get a (linear) deformation retraction, with M being fixed during the homotopy.
The original interest in sets of positive reach lies in the fact that they have suitable small parallel neighborhoods with no self-intersections which allow one to compute their volume. This leads to a Steiner-type formula and a definition of curvature measures for these sets (see [Reference Thale38]). If M is a compact Riemannian submanifold in
![]() ${\mathbb R}^d$
, as considered in [Reference Niyogi, Smale and Weinberger33], then
${\mathbb R}^d$
, as considered in [Reference Niyogi, Smale and Weinberger33], then
![]() $\tau (M)$
is positive and is the largest number having the property that the open normal bundle about M of radius r is smoothly embedded in
$\tau (M)$
is positive and is the largest number having the property that the open normal bundle about M of radius r is smoothly embedded in
![]() ${\mathbb R}^d$
for every
${\mathbb R}^d$
for every
![]() $r < \tau$
. It is enough, however, for M to be
$r < \tau$
. It is enough, however, for M to be
![]() $C^2$
to ensure that
$C^2$
to ensure that
![]() $\tau (M)>0$
(see [Reference Thale38, Proposition 14]), and it is even enough for it to be
$\tau (M)>0$
(see [Reference Thale38, Proposition 14]), and it is even enough for it to be
![]() $C^{1,1}$
in the case that M is a closed hypersurface (see [Reference Scholtes36, Theorem 1.3], which is an if-and-only-if statement). We recall the definition of
$C^{1,1}$
in the case that M is a closed hypersurface (see [Reference Scholtes36, Theorem 1.3], which is an if-and-only-if statement). We recall the definition of
![]() $C^{1,1}$
(see [Reference Hörmander24, Definition 2.4.2]).
$C^{1,1}$
(see [Reference Hörmander24, Definition 2.4.2]).
Definition 2.1. A closed manifold
![]() $M\subset{\mathbb R}^d$
is said to have
$M\subset{\mathbb R}^d$
is said to have
![]() $C^{1,1}$
boundary
$C^{1,1}$
boundary
![]() $\partial M$
if for every
$\partial M$
if for every
![]() $x_0\in\partial M$
one can find a local open chart U of
$x_0\in\partial M$
one can find a local open chart U of
![]() $x_0\in \partial M$
, and coordinates with the origin at
$x_0\in \partial M$
, and coordinates with the origin at
![]() $x_0$
, such that
$x_0$
, such that
![]() $U\cap M = \{x\in M\ |\ x_1\geq f(x')\}$
, where
$U\cap M = \{x\in M\ |\ x_1\geq f(x')\}$
, where
![]() $x'=(x_2,\ldots, x_d)$
, f is
$x'=(x_2,\ldots, x_d)$
, f is
![]() $C^1$
, and grad(f) is Lipschitz continuous.
$C^1$
, and grad(f) is Lipschitz continuous.
Crucial to us in this section are the next two results. For general discussion, we refer to [Reference Federer17, Reference Fu19] for Proposition 2.1, and [Reference Barb4, Reference Scholtes36] for Proposition 2.2. Throughout, a manifold is assumed to be compact, and without boundary unless we specify the contrary. For
![]() $x\in{\mathbb R}^d$
, let
$x\in{\mathbb R}^d$
, let
![]() $d_M(x )=d(x , M ) = \hbox{inf} \{d(x,y), y \in M\}$
be the distance function to M. This function is 1-Lipschitz, and it is continuously differentiable when restricted to the interior of
$d_M(x )=d(x , M ) = \hbox{inf} \{d(x,y), y \in M\}$
be the distance function to M. This function is 1-Lipschitz, and it is continuously differentiable when restricted to the interior of
![]() $M^{\oplus r}\setminus M$
if
$M^{\oplus r}\setminus M$
if
![]() $r<\tau$
(see [Reference Federer17, Theorem 4.8]). Elementary point-set topology shows that the interior of the r-offset of M is
$r<\tau$
(see [Reference Federer17, Theorem 4.8]). Elementary point-set topology shows that the interior of the r-offset of M is
![]() $\hbox{int}(M^{\oplus r}) = \bigcup_{x\in M}\mathring{B}(x,r) = d^{-1}_M[0,r)$
, and the topological boundary is
$\hbox{int}(M^{\oplus r}) = \bigcup_{x\in M}\mathring{B}(x,r) = d^{-1}_M[0,r)$
, and the topological boundary is
![]() $d_M^{-1}(r)$
.
$d_M^{-1}(r)$
.
Proposition 2.1. ([Reference Federer17].) Let
![]() $M\subset{\mathbb R}^d$
be compact of positive reach
$M\subset{\mathbb R}^d$
be compact of positive reach
![]() $\tau$
. For
$\tau$
. For
![]() $0<r <\tau$
,
$0<r <\tau$
,
![]() $M^{\oplus r}$
is a compact manifold with
$M^{\oplus r}$
is a compact manifold with
![]() $C^{1,1}$
boundary.
$C^{1,1}$
boundary.
We next describe tubular neighborhoods of a
![]() $C^{1,1}$
-submanifold.
$C^{1,1}$
-submanifold.
Proposition 2.2. A closed submanifold N in
![]() ${\mathbb R}^d$
,
${\mathbb R}^d$
,
![]() $d\geq 2$
, has a tubular neighborhood ‘foliated by orthogonal disks’ if and only if it is
$d\geq 2$
, has a tubular neighborhood ‘foliated by orthogonal disks’ if and only if it is
![]() $C^{1,1}$
.
$C^{1,1}$
.
Proof. This is a consequence of [Reference Scholtes36, Theorem 1.3], which proves that N is
![]() $C^{1,1}$
if and only if it has positive reach
$C^{1,1}$
if and only if it has positive reach
![]() $\tau$
. A tubular neighborhood T (i.e. an embedding of the normal bundle extending the embedding of M) consists of all points at a distance strictly less than
$\tau$
. A tubular neighborhood T (i.e. an embedding of the normal bundle extending the embedding of M) consists of all points at a distance strictly less than
![]() $\tau$
from N. This neighborhood has a unique nearest point projection
$\tau$
from N. This neighborhood has a unique nearest point projection
![]() $\pi_M\;:\; T\rightarrow M$
. The orthogonal disks are the preimages of points in M under
$\pi_M\;:\; T\rightarrow M$
. The orthogonal disks are the preimages of points in M under
![]() $\pi_M$
.
$\pi_M$
.
Remark 2.2. A very informative discussion about the above is on MathOverflow [31], and the point is this. In the
![]() $C^1$
case, the choice of the (unit, outer) normal vector at every point of N is a continuous function (this is by definition the Gauss map). In fact if N is
$C^1$
case, the choice of the (unit, outer) normal vector at every point of N is a continuous function (this is by definition the Gauss map). In fact if N is
![]() $C^k$
, then the choice of a normal
$C^k$
, then the choice of a normal
![]() $N\rightarrow{\mathbb R}^n$
is
$N\rightarrow{\mathbb R}^n$
is
![]() $C^{k-1}$
(see [Reference Barb4, Lemma 4.6.18]). If we have
$C^{k-1}$
(see [Reference Barb4, Lemma 4.6.18]). If we have
![]() $C^1$
-regularity but not
$C^1$
-regularity but not
![]() $C^{1,1}$
, it could happen that the normals intersect arbitrarily close to the hypersurface, in which case the reach is indeed 0. A good example to keep in mind, which we owe to S. Scholtes (private communication), is the graph of the real-valued function which is 0 for
$C^{1,1}$
, it could happen that the normals intersect arbitrarily close to the hypersurface, in which case the reach is indeed 0. A good example to keep in mind, which we owe to S. Scholtes (private communication), is the graph of the real-valued function which is 0 for
![]() $x\leq 0$
and
$x\leq 0$
and
![]() $x^{3/2}$
for
$x^{3/2}$
for
![]() $x\geq 0$
. This function is
$x\geq 0$
. This function is
![]() $C^{1, {1/2}}$
, not
$C^{1, {1/2}}$
, not
![]() $C^{1,1}$
, and one observes that near 0, the normals intersect arbitrarily close to the curve.
$C^{1,1}$
, and one observes that near 0, the normals intersect arbitrarily close to the curve.
If M is a compact PR set, its offset
![]() $M^{\oplus r}$
is also compact and PR for
$M^{\oplus r}$
is also compact and PR for
![]() $r<\tau$
, with reach
$r<\tau$
, with reach
![]() $\tau-r$
, where
$\tau-r$
, where
![]() $\tau$
is the reach of M. This assertion is not entirely obvious, since, in general, the reach is not always well-behaved for nested compact sets. By this we mean that if
$\tau$
is the reach of M. This assertion is not entirely obvious, since, in general, the reach is not always well-behaved for nested compact sets. By this we mean that if
![]() $(K_2,K_1)$
is a pair of nested compact sets in
$(K_2,K_1)$
is a pair of nested compact sets in
![]() ${\mathbb R}^d$
,
${\mathbb R}^d$
,
![]() $K_1\subset K_2$
, then both cases
$K_1\subset K_2$
, then both cases
![]() $\tau_1<\tau_2$
or
$\tau_1<\tau_2$
or
![]() $\tau_2<\tau_1$
can occur, where
$\tau_2<\tau_1$
can occur, where
![]() $\tau_i$
is the reach of
$\tau_i$
is the reach of
![]() $K_i$
. As an example of the former case, take
$K_i$
. As an example of the former case, take
![]() $K_1$
to be the circle and
$K_1$
to be the circle and
![]() $K_2$
to be the closed disk; for the latter case, take
$K_2$
to be the closed disk; for the latter case, take
![]() $K_1$
to be a point in a finite-reach
$K_1$
to be a point in a finite-reach
![]() $K_2$
. The case of
$K_2$
. The case of
![]() $(K_2,K_1) = (M^{\oplus r}, M)$
is therefore special.
$(K_2,K_1) = (M^{\oplus r}, M)$
is therefore special.
Lemma 2.3. Let
![]() $M\subset{\mathbb R}^d$
be a compact PR set with reach
$M\subset{\mathbb R}^d$
be a compact PR set with reach
![]() $\tau$
, and
$\tau$
, and
![]() $0\leq r<\tau$
; then
$0\leq r<\tau$
; then
![]() $M^{\oplus r}$
has positive reach with
$M^{\oplus r}$
has positive reach with
![]() $\tau (M^{\oplus r})=\tau-r>0$
.
$\tau (M^{\oplus r})=\tau-r>0$
.
Proof. Essentially, the point is that any ray from
![]() $y\not\in M^{\oplus r}$
to M must cut the boundary
$y\not\in M^{\oplus r}$
to M must cut the boundary
![]() $\partial M^{\oplus r}$
at a point lying at a distance of r to M. Suppose
$\partial M^{\oplus r}$
at a point lying at a distance of r to M. Suppose
![]() $r>0$
, so that
$r>0$
, so that
![]() $M^{\oplus r}$
is a codimension-0 manifold with boundary
$M^{\oplus r}$
is a codimension-0 manifold with boundary
![]() $\partial M^{\oplus r}$
in
$\partial M^{\oplus r}$
in
![]() ${\mathbb R}^d$
. Write
${\mathbb R}^d$
. Write
![]() $\tau_r$
for its reach. We will first prove that if y in the complement of
$\tau_r$
for its reach. We will first prove that if y in the complement of
![]() $M^{\oplus r}$
has a unique projection onto M, then necessarily it has a unique projection onto
$M^{\oplus r}$
has a unique projection onto M, then necessarily it has a unique projection onto
![]() $M^{\oplus r}$
(this will prove that
$M^{\oplus r}$
(this will prove that
![]() $\tau_r>0$
and that
$\tau_r>0$
and that
![]() $\tau - r\leq \tau_r$
). Reciprocally, we will argue that if y has a unique projection onto M, then it also has a unique projection onto
$\tau - r\leq \tau_r$
). Reciprocally, we will argue that if y has a unique projection onto M, then it also has a unique projection onto
![]() $M^{\oplus r}$
.
$M^{\oplus r}$
.
To prove the first claim, write
![]() $y_1 = [y,\pi_M(y)]\cap\partial M^{\oplus r}$
. We claim that
$y_1 = [y,\pi_M(y)]\cap\partial M^{\oplus r}$
. We claim that
![]() $y_1$
is the unique closest point to y in
$y_1$
is the unique closest point to y in
![]() $M^{\oplus r}$
. Indeed, if there is
$M^{\oplus r}$
. Indeed, if there is
![]() $z_1$
on that boundary that is closer to y, then
$z_1$
on that boundary that is closer to y, then
and so
![]() $d(y,\pi_M(z_1))=d(y,\pi_M(y))$
(since
$d(y,\pi_M(z_1))=d(y,\pi_M(y))$
(since
![]() $d(y,\pi_M(y))$
is smallest distance from y to M), and by uniqueness,
$d(y,\pi_M(y))$
is smallest distance from y to M), and by uniqueness,
![]() $\pi_M(z_1)=\pi_M(y)$
. This implies that
$\pi_M(z_1)=\pi_M(y)$
. This implies that
![]() $d(y,z_1) + d(z_1,M)=d(y,M)$
, and so
$d(y,z_1) + d(z_1,M)=d(y,M)$
, and so
![]() $y,z_1,\pi_M(y)$
are aligned. This can only happen if
$y,z_1,\pi_M(y)$
are aligned. This can only happen if
![]() $y_1=z_1$
.
$y_1=z_1$
.
Suppose now that y has a unique projection onto
![]() $M^{\oplus r}$
, which we label y’. We can check that it also has a unique projection onto M. Let z be that projection. By a similar argument as previously, z must be
$M^{\oplus r}$
, which we label y’. We can check that it also has a unique projection onto M. Let z be that projection. By a similar argument as previously, z must be
![]() $\pi_M(y')$
(so unique) and y, y’,z are aligned. This shows reciprocally that
$\pi_M(y')$
(so unique) and y, y’,z are aligned. This shows reciprocally that
![]() $\tau_r+r\leq \tau$
.
$\tau_r+r\leq \tau$
.
The above arguments show that
![]() $\tau = \tau_r+r$
, and in fact they can be used to show in this case that
$\tau = \tau_r+r$
, and in fact they can be used to show in this case that
![]() $M^{\oplus r'}= (M^{\oplus r})^{\oplus (r'-r)} $
for all
$M^{\oplus r'}= (M^{\oplus r})^{\oplus (r'-r)} $
for all
![]() $r\leq r'< \tau$
.
$r\leq r'< \tau$
.
2.2. Manifolds with boundary
In order to apply our ideas to PR sets, we need to extend Theorem 2.1 from closed Riemannian submanifolds to submanifolds with boundary. Note that the reach of
![]() $\partial M$
(manifold boundary) and M are not comparable in general. Indeed, take M to be the
$\partial M$
(manifold boundary) and M are not comparable in general. Indeed, take M to be the
![]() $y=\sin (x)$
curve on
$y=\sin (x)$
curve on
![]() $[0,\pi]$
, with boundary the endpoints. Then
$[0,\pi]$
, with boundary the endpoints. Then
![]() $\tau (M) < \tau (\partial M)$
. Take now a closed disk M in
$\tau (M) < \tau (\partial M)$
. Take now a closed disk M in
![]() ${\mathbb R}^2$
. Then
${\mathbb R}^2$
. Then
![]() $\tau (\partial M)<\tau (M)=\infty$
. If M is of codimension 0, then
$\tau (\partial M)<\tau (M)=\infty$
. If M is of codimension 0, then
![]() $\tau (\partial M)\leq\tau (M)$
always.
$\tau (\partial M)\leq\tau (M)$
always.
In [Reference Wang and Wang39], the authors managed to extend Theorem 2.1 to smooth submanifolds with boundary and showed that in this case the bound
![]() $\sqrt\frac{3}{5}\tau$
in Theorem 2.1 can be replaced by
$\sqrt\frac{3}{5}\tau$
in Theorem 2.1 can be replaced by
![]() $\frac{\delta}{2}$
, where
$\frac{\delta}{2}$
, where
![]() $\delta = \min (\tau (M), \tau (\partial M))$
. We revisit this result in the codimension-0 case and establish the following ‘twice the density, half the reach’ criterion.
$\delta = \min (\tau (M), \tau (\partial M))$
. We revisit this result in the codimension-0 case and establish the following ‘twice the density, half the reach’ criterion.
Proposition 2.3. Let M be a compact codimension-0 submanifold of
![]() ${\mathbb R}^d$
with
${\mathbb R}^d$
with
![]() $C^{1,1}$
boundary and having positive reach
$C^{1,1}$
boundary and having positive reach
![]() $\tau=\tau (M)>0$
, and let
$\tau=\tau (M)>0$
, and let
![]() $S \subset M$
be an
$S \subset M$
be an
![]() $\frac{\epsilon}{2}$
-dense finite subset with
$\frac{\epsilon}{2}$
-dense finite subset with
![]() $\epsilon < \frac{\tau}{2}$
. Then for any r such that
$\epsilon < \frac{\tau}{2}$
. Then for any r such that
![]() $\epsilon\leq r< \frac{\tau}{2}$
,
$\epsilon\leq r< \frac{\tau}{2}$
,
![]() ${M\overset{\simeq}{\longrightarrow}\bigcup_{x\in S }{B}(x,r)}$
.
${M\overset{\simeq}{\longrightarrow}\bigcup_{x\in S }{B}(x,r)}$
.
Notice that M need not be connected. Notice also that we have weakened the regularity on
![]() $\partial M$
from smooth to
$\partial M$
from smooth to
![]() $C^{1,1}$
. According to [Reference Scholtes36, Theorem 1.3] (see also [Reference Federer17, Remark 4.20]), this condition is enough to ensure that
$C^{1,1}$
. According to [Reference Scholtes36, Theorem 1.3] (see also [Reference Federer17, Remark 4.20]), this condition is enough to ensure that
![]() $\tau (\partial M)>0$
. Finally, notice that we use closed balls in our statement, and that they may have radius larger than
$\tau (\partial M)>0$
. Finally, notice that we use closed balls in our statement, and that they may have radius larger than
![]() $\epsilon$
, but not exceeding
$\epsilon$
, but not exceeding
![]() $\frac{\tau}{2}$
.
$\frac{\tau}{2}$
.
Proof. The proof is an adaptation of Lemma 4.1 of [Reference Niyogi, Smale and Weinberger33] and Lemma 4.3 of [Reference Wang and Wang39] for smooth submanifolds. For completeness, we will reconstruct the part of the argument that we need.
Firstly, since the reach of a disjoint finite union of PR sets is the least of their reaches and their pairwise distances, we can assume without loss of generality that M is connected from the start. Let M be connected of codimension 0. Then its boundary is a connected codimension-1 closed submanifold (i.e. a closed hypersurface). It divides Euclidean space into two regions: M and its complement. We let
![]() $\tau^-$
denote the reach of a component of
$\tau^-$
denote the reach of a component of
![]() $\partial M$
in M (the interior region), and
$\partial M$
in M (the interior region), and
![]() $\tau^+$
its reach within the open (exterior) region. Clearly
$\tau^+$
its reach within the open (exterior) region. Clearly
![]() $\tau\;:\!=\;\tau (M)=\tau^+$
.
$\tau\;:\!=\;\tau (M)=\tau^+$
.
Now
![]() $\partial M$
is
$\partial M$
is
![]() $C^{1,1}$
by hypothesis, and being a closed hypersurface, it is necessarily orientable. It has a continuous normal vector field into the exterior region, defining a (trivial)
$C^{1,1}$
by hypothesis, and being a closed hypersurface, it is necessarily orientable. It has a continuous normal vector field into the exterior region, defining a (trivial)
![]() ${\mathbb R}_+$
-bundle
${\mathbb R}_+$
-bundle
![]() $T(\partial M)^+$
of
$T(\partial M)^+$
of
![]() $T(\partial M)$
. We write
$T(\partial M)$
. We write
![]() $T_p^{\perp,+}(\partial M)$
for the fiber at
$T_p^{\perp,+}(\partial M)$
for the fiber at
![]() $p\in\partial M$
, which is a half-line extending into the exterior region, perpendicular to
$p\in\partial M$
, which is a half-line extending into the exterior region, perpendicular to
![]() $T_p(\partial M)$
. Linear deformation retraction along this direction as in Lemma 2.2, keeping M fixed, shows that
$T_p(\partial M)$
. Linear deformation retraction along this direction as in Lemma 2.2, keeping M fixed, shows that
![]() ${M\overset{\simeq}{\longrightarrow}M^{\oplus r}}$
as long as
${M\overset{\simeq}{\longrightarrow}M^{\oplus r}}$
as long as
![]() $r<\tau^+=\tau $
(where normal directions never intersect). We have that
$r<\tau^+=\tau $
(where normal directions never intersect). We have that
We want to show that this retraction of
![]() $M^{\oplus r}$
onto M (along fibers of
$M^{\oplus r}$
onto M (along fibers of
![]() $T^+(\partial M)$
) restricts to a deformation retraction onto M of the middle space
$T^+(\partial M)$
) restricts to a deformation retraction onto M of the middle space
![]() $S^{\oplus r}$
in the sequence of inclusions below:
$S^{\oplus r}$
in the sequence of inclusions below:
That is, we only take the union of balls centered at points of S. This covers M since
![]() $r\geq \frac{\epsilon}{2}$
and any point of M is within distance
$r\geq \frac{\epsilon}{2}$
and any point of M is within distance
![]() $\epsilon/2$
of S. Let us see how the deformation retraction of the bigger space
$\epsilon/2$
of S. Let us see how the deformation retraction of the bigger space
![]() $M^{\oplus r}$
onto M may fail to restrict to a retraction on
$M^{\oplus r}$
onto M may fail to restrict to a retraction on
![]() $S^{\oplus r}$
: let
$S^{\oplus r}$
: let
![]() $v\in T_p^{\perp,+}(\partial M)$
, and suppose
$v\in T_p^{\perp,+}(\partial M)$
, and suppose
![]() $v\in B(q,r)$
, with
$v\in B(q,r)$
, with
![]() $q\in S$
but
$q\in S$
but
![]() $q\not\in B(p,r)$
. So the line segment [v, p] is not in the ball B(q, r), and the linear retraction will leave that ball eventually. This, however, will not cause a problem as long as the segment falls in another ball and does not leave the entire union
$q\not\in B(p,r)$
. So the line segment [v, p] is not in the ball B(q, r), and the linear retraction will leave that ball eventually. This, however, will not cause a problem as long as the segment falls in another ball and does not leave the entire union
![]() $\bigcup_{x\in S}B(x,r)$
. This happens if both v and p are in some other ball B(x, r),
$\bigcup_{x\in S}B(x,r)$
. This happens if both v and p are in some other ball B(x, r),
![]() $x\in S$
(because balls are convex). By the density condition, we can also demand that x be at a distance of at most
$x\in S$
(because balls are convex). By the density condition, we can also demand that x be at a distance of at most
![]() $\frac{\epsilon}{2}$
from p. To recapitulate, for every such p, v, by picking an
$\frac{\epsilon}{2}$
from p. To recapitulate, for every such p, v, by picking an
![]() $x\in S$
within a distance of
$x\in S$
within a distance of
![]() $\frac{\epsilon}{2}$
from p and a distance of r from v, we guarantee that the deformation retraction of
$\frac{\epsilon}{2}$
from p and a distance of r from v, we guarantee that the deformation retraction of
![]() $M^{\oplus r}$
restricts to
$M^{\oplus r}$
restricts to
![]() $S^{\oplus r}$
(see Figure 2).
$S^{\oplus r}$
(see Figure 2).

Figure 2.
![]() $M\subset{\mathbb R}^d$
is represented by the shaded area,
$M\subset{\mathbb R}^d$
is represented by the shaded area,
![]() $p,q\in\partial M$
, and
$p,q\in\partial M$
, and
![]() $x,q\in S$
. The points q, p are on a circle tangent to
$x,q\in S$
. The points q, p are on a circle tangent to
![]() $T_p(M)$
, having radius
$T_p(M)$
, having radius
![]() $\tau$
and center on the vertical dashed line representing the normal direction
$\tau$
and center on the vertical dashed line representing the normal direction
![]() $T_p^{\perp,+}(M)$
, pointing into the exterior region, while x is anywhere in
$T_p^{\perp,+}(M)$
, pointing into the exterior region, while x is anywhere in
![]() $M\cap S$
at a distance of at most
$M\cap S$
at a distance of at most
![]() $\frac{\epsilon}{2}$
from p. An extreme disposition of such points (meaning when v is as far as possible from x) happens when v, p, x are aligned. This figure is the analog of Figure 2 of [Reference Niyogi, Smale and Weinberger33] and Figure 1 of [Reference Wang and Wang39].
$\frac{\epsilon}{2}$
from p. An extreme disposition of such points (meaning when v is as far as possible from x) happens when v, p, x are aligned. This figure is the analog of Figure 2 of [Reference Niyogi, Smale and Weinberger33] and Figure 1 of [Reference Wang and Wang39].
With the above target in mind, consider the following configuration of points:
![]() $p\in\partial M$
,
$p\in\partial M$
,
![]() $v\in T_p^{\perp,+}(\partial M)\cap B(p,\tau)$
,
$v\in T_p^{\perp,+}(\partial M)\cap B(p,\tau)$
,
![]() $q\in S$
, and
$q\in S$
, and
![]() $v\in B(q,r)$
but
$v\in B(q,r)$
but
![]() $p\not\in B(q,r)$
. How far can v be from p, among all choices of such points q? The answer can be extracted from the key Lemma 4.1 of [Reference Niyogi, Smale and Weinberger33]. The worst-case scenario, corresponding to when v would be farthest from p, is when q and p lie on the circle of radius
$p\not\in B(q,r)$
. How far can v be from p, among all choices of such points q? The answer can be extracted from the key Lemma 4.1 of [Reference Niyogi, Smale and Weinberger33]. The worst-case scenario, corresponding to when v would be farthest from p, is when q and p lie on the circle of radius
![]() $\tau$
, with center in
$\tau$
, with center in
![]() $T_p^{\perp,+}$
as in Figure 2, and p,q,v make up an isosceles triangle with
$T_p^{\perp,+}$
as in Figure 2, and p,q,v make up an isosceles triangle with
![]() $|p-q|=|q-v|=r$
. Lemma 4.1 of [Reference Niyogi, Smale and Weinberger33] applied to this situation gives that
$|p-q|=|q-v|=r$
. Lemma 4.1 of [Reference Niyogi, Smale and Weinberger33] applied to this situation gives that
![]() $\displaystyle d(v,p)< \frac{r^2}{\tau^+} = \frac{r^2}{\tau} <\tau$
.
$\displaystyle d(v,p)< \frac{r^2}{\tau^+} = \frac{r^2}{\tau} <\tau$
.
Next, we look for an
![]() $x\in B(p,\frac{\epsilon}{2})\cap S\neq\emptyset$
which is within distance r of v. By the triangle inequality,
$x\in B(p,\frac{\epsilon}{2})\cap S\neq\emptyset$
which is within distance r of v. By the triangle inequality,
![]() $\displaystyle d(x,v)\leq d(x,p)+d(p,v)\leq \frac{\epsilon}{2} + \frac{r^2}{\tau}$
, and so in order for
$\displaystyle d(x,v)\leq d(x,p)+d(p,v)\leq \frac{\epsilon}{2} + \frac{r^2}{\tau}$
, and so in order for
![]() $v\in B(x,r)$
, it is enough to require that
$v\in B(x,r)$
, it is enough to require that
Any value of r between the roots of the polynomial on the right-hand side does the job, and it is immediate that
![]() $r\in \left[\epsilon, \frac{\tau}{2}\right[$
satisfies this condition. The proof is complete.
$r\in \left[\epsilon, \frac{\tau}{2}\right[$
satisfies this condition. The proof is complete.
Note that in the case of Theorem 2.1 in [Reference Niyogi, Smale and Weinberger33], that is, when one is considering M that is closed (i.e. with no boundary), the point x to be chosen cannot simply be ‘anywhere’ around
![]() $p\in M$
, as in Figure 2, but must lie on M (which would be the boundary in that figure), and thus the authors get a different bound on r.
$p\in M$
, as in Figure 2, but must lie on M (which would be the boundary in that figure), and thus the authors get a different bound on r.
We finally come to the proof of the main reconstruction result of this section, which yields Theorem 1.2 as a consequence. We thank the referee for suggesting this statement, which is simpler than the one we originally gave.
Theorem 2.2. Let M be a compact space in
![]() ${\mathbb R}^d$
with positive reach
${\mathbb R}^d$
with positive reach
![]() $\tau$
, let
$\tau$
, let
![]() $\epsilon\in \left(0, \frac{\tau}{2}\right)$
, and let
$\epsilon\in \left(0, \frac{\tau}{2}\right)$
, and let
![]() $r\in \left(\epsilon, \frac{\tau}{2}\right)$
. If
$r\in \left(\epsilon, \frac{\tau}{2}\right)$
. If
![]() $S\subset M$
is
$S\subset M$
is
![]() $\frac{\epsilon}{2}$
-dense, then
$\frac{\epsilon}{2}$
-dense, then
![]() $\displaystyle M\overset{\simeq}{\longrightarrow}\bigcup_{x\in S }B(x,r)$
.
$\displaystyle M\overset{\simeq}{\longrightarrow}\bigcup_{x\in S }B(x,r)$
.
Proof. Notice that by Proposition 2.3, the result is true if M is a codimension-0 submanifold whose boundary is
![]() $C^{1,1}$
of reach
$C^{1,1}$
of reach
![]() $\tau>0$
(let us refer to this submanifold as a ‘good object’). The idea now is very simple and relies on the fact that, if M itself is not such a good object but is of positive reach, then any slight thickening of it will be a good object.
$\tau>0$
(let us refer to this submanifold as a ‘good object’). The idea now is very simple and relies on the fact that, if M itself is not such a good object but is of positive reach, then any slight thickening of it will be a good object.
Assume that S is
![]() $\epsilon/2$
-dense in M, with
$\epsilon/2$
-dense in M, with
![]() $\epsilon < \frac{\tau}{2}$
. We first collect the following facts:
$\epsilon < \frac{\tau}{2}$
. We first collect the following facts:
-
1. For
 $0<\delta<\tau$
,
$0<\delta<\tau$
,
 $M^{\oplus\delta}$
deformation retracts onto M (Lemma 2.2).
$M^{\oplus\delta}$
deformation retracts onto M (Lemma 2.2). -
2. For
 $0<\delta<\tau$
, S is
$0<\delta<\tau$
, S is
 $\left(\frac{\epsilon}{2}+\delta\right)$
-dense in
$\left(\frac{\epsilon}{2}+\delta\right)$
-dense in
 $M^{\oplus\delta}\supset M$
.
$M^{\oplus\delta}\supset M$
. -
3. The offset
 $M^{\oplus\delta}$
is a codimension-0 submanifold of
$M^{\oplus\delta}$
is a codimension-0 submanifold of
 ${\mathbb R}^d$
, with
${\mathbb R}^d$
, with
 $C^{1,1}$
boundary (Proposition 2.1). Its reach is
$C^{1,1}$
boundary (Proposition 2.1). Its reach is
 $\tau'=\tau-\delta$
(Lemma 2.3).
$\tau'=\tau-\delta$
(Lemma 2.3).
Assume that
![]() $\displaystyle\delta < \frac{\tau-2\epsilon}{5}$
. This is equivalent to
$\displaystyle\delta < \frac{\tau-2\epsilon}{5}$
. This is equivalent to
![]() $\epsilon + 2\delta < \frac{\tau - \delta}{2}$
; that is, twice the density of S in
$\epsilon + 2\delta < \frac{\tau - \delta}{2}$
; that is, twice the density of S in
![]() $M^{\oplus\delta}$
is less than half the reach of
$M^{\oplus\delta}$
is less than half the reach of
![]() $M^{\oplus\delta}$
. By Proposition 2.3, for all r that we can insert between these two numbers, we get a homotopy reconstruction of
$M^{\oplus\delta}$
. By Proposition 2.3, for all r that we can insert between these two numbers, we get a homotopy reconstruction of
![]() $M^{\oplus\delta}$
; more precisely,
$M^{\oplus\delta}$
; more precisely,
Returning to the hypotheses of Theorem 2.2, choose any r such that
![]() $\epsilon< r<\frac{\tau}{2}$
. Pick
$\epsilon< r<\frac{\tau}{2}$
. Pick
![]() $\delta$
such that
$\delta$
such that
![]() $\displaystyle 0<\delta < \min\left\{\frac{r - \epsilon}{2}, \tau -2r\right\}$
. For this
$\displaystyle 0<\delta < \min\left\{\frac{r - \epsilon}{2}, \tau -2r\right\}$
. For this
![]() $\delta$
,
$\delta$
,
![]() $\epsilon+2\delta\leq r$
and
$\epsilon+2\delta\leq r$
and
![]() $r< \frac{\tau-\delta}{2}$
, and thus by (2.5),
$r< \frac{\tau-\delta}{2}$
, and thus by (2.5),
![]() $\bigcup_{x\in S }B(x,r)$
deformation retracts onto
$\bigcup_{x\in S }B(x,r)$
deformation retracts onto
![]() $M^{\oplus\delta}$
. Since the latter deformation retracts onto M, the composition of both retractions shows that
$M^{\oplus\delta}$
. Since the latter deformation retracts onto M, the composition of both retractions shows that
![]() ${M\overset{\simeq}{\longrightarrow}\bigcup_{x\in S }B(x,r)}$
. The proof is complete.
${M\overset{\simeq}{\longrightarrow}\bigcup_{x\in S }B(x,r)}$
. The proof is complete.
3. Blocking techniques and upper bounds for the Hausdorff distance
In this section we state and prove the main technical result of this paper. This is given by Proposition 3.1 below, which is general and of independent interest. It is based on blocking techniques as well as a useful geometrical result, proven in [Reference Niyogi, Smale and Weinberger33], relating the minimal covering number of a compact set by closed balls to the maximal length of a chain of points whose pairwise distances are bounded below.
Let
![]() (where
(where
![]() is either
is either
![]() ${\mathbb Z}$
,
${\mathbb Z}$
,
![]() $\mathrm{I\!N}$
, or
$\mathrm{I\!N}$
, or
![]() $\mathrm{I\!N}\setminus \{0\}$
) be a stationary sequence of
$\mathrm{I\!N}\setminus \{0\}$
) be a stationary sequence of
![]() $\mathrm{I\!R}^d$
-valued random variables. Let P be the distribution of
$\mathrm{I\!R}^d$
-valued random variables. Let P be the distribution of
![]() $X_1$
. Suppose that P is supported on a compact set
$X_1$
. Suppose that P is supported on a compact set
![]() $\mathrm{I\!M}$
of
$\mathrm{I\!M}$
of
![]() $\mathrm{I\!R}^d$
, i.e.
$\mathrm{I\!R}^d$
, i.e.
![]() $\mathrm{I\!M} \;:\!=\; {\mbox{supp}} (X_j)$
is the smallest closed set carrying the mass of P:
$\mathrm{I\!M} \;:\!=\; {\mbox{supp}} (X_j)$
is the smallest closed set carrying the mass of P:
where
![]() $\overline{C}$
means the closure of the set C in Euclidean space. Recall that
$\overline{C}$
means the closure of the set C in Euclidean space. Recall that
![]() ${\mathbb X}_n=\{X_1,\cdots,X_n\}$
and this is viewed as a subset of
${\mathbb X}_n=\{X_1,\cdots,X_n\}$
and this is viewed as a subset of
![]() $\mathrm{I\!R}^d$
. Throughout, we will be working with the Hausdorff distance
$\mathrm{I\!R}^d$
. Throughout, we will be working with the Hausdorff distance
![]() $d_H$
(2.1). Note that
$d_H$
(2.1). Note that
![]() $d_H(\{x\},\{y\})=||x-y||$
(in the Euclidean distance) if x, y are points. Note that the distance of a point y to a closed set A is
$d_H(\{x\},\{y\})=||x-y||$
(in the Euclidean distance) if x, y are points. Note that the distance of a point y to a closed set A is
![]() $d(y,A)=\inf_{x\in A}||x-y||$
, while its Hausdorff distance to A is
$d(y,A)=\inf_{x\in A}||x-y||$
, while its Hausdorff distance to A is
![]() $d_H(y,A) = \sup_{x\in A}||x-y||$
. This explains in part why this metric is very sensitive to outliers (see [Reference Moreno, Koppal and de Muinck32]) and to noisy phenomena.
$d_H(y,A) = \sup_{x\in A}||x-y||$
. This explains in part why this metric is very sensitive to outliers (see [Reference Moreno, Koppal and de Muinck32]) and to noisy phenomena.
We wish to give upper bounds for
![]() $\mathrm{I\!P}\!\left(d_H({\mathbb X}_n, \mathrm{I\!M})> \epsilon\right)$
via a blocking technique. Let k and r be two positive integers such that
$\mathrm{I\!P}\!\left(d_H({\mathbb X}_n, \mathrm{I\!M})> \epsilon\right)$
via a blocking technique. Let k and r be two positive integers such that
![]() $kr\leq n$
. For
$kr\leq n$
. For
![]() $1\leq i\leq k$
, define the random vector
$1\leq i\leq k$
, define the random vector
![]() $Y_{i,r}$
in
$Y_{i,r}$
in
![]() $\mathrm{I\!R}^{dr}$
by
$\mathrm{I\!R}^{dr}$
by
![]() $Y_{i,r}=(X_{(i-1)r+1},\cdots,X_{ir})^t.$
Let
$Y_{i,r}=(X_{(i-1)r+1},\cdots,X_{ir})^t.$
Let
be a subset in
![]() $\mathrm{I\!R}^{dr}$
of k stationary random vectors which are not necessarily independent. The support
$\mathrm{I\!R}^{dr}$
of k stationary random vectors which are not necessarily independent. The support
![]() $\mathrm{I\!M}_{dr}$
of the vector
$\mathrm{I\!M}_{dr}$
of the vector
![]() $Y_{1,r}$
is included in
$Y_{1,r}$
is included in
![]() $\mathrm{I\!M}\times \cdots \times\mathrm{I\!M}$
(r times), and since, by definition,
$\mathrm{I\!M}\times \cdots \times\mathrm{I\!M}$
(r times), and since, by definition,
![]() $\mathrm{I\!M}_{dr}$
is a closed set, it is necessarily compact in
$\mathrm{I\!M}_{dr}$
is a closed set, it is necessarily compact in
![]() $\mathrm{I\!R}^{dr}$
. As we now show, it is possible to reduce the behavior of
$\mathrm{I\!R}^{dr}$
. As we now show, it is possible to reduce the behavior of
![]() $d_H({\mathbb X}_n , {\mathrm{I\!M}})$
to that of the sequence of vectors
$d_H({\mathbb X}_n , {\mathrm{I\!M}})$
to that of the sequence of vectors
![]() $(Y_{i,r})_{1\leq i\leq k}$
for any k and r for which
$(Y_{i,r})_{1\leq i\leq k}$
for any k and r for which
![]() $kr\leq n$
and under only the assumption of stationarity of
$kr\leq n$
and under only the assumption of stationarity of
![]() .
.
Proposition 3.1. With
![]() $\epsilon>0$
, and with k and r any positive integers such that
$\epsilon>0$
, and with k and r any positive integers such that
![]() $kr\leq n$
, it holds that
$kr\leq n$
, it holds that
Proof. Since
![]() $\mathrm{I\!P}\!\left({\mathbb Y}_{k} \subset {\mathrm{I\!M}}_{dr}\right)=1$
, we have almost surely (a.s.)
$\mathrm{I\!P}\!\left({\mathbb Y}_{k} \subset {\mathrm{I\!M}}_{dr}\right)=1$
, we have almost surely (a.s.)
Since
![]() ${\mathrm{I\!M}}_{dr}$
is compact, there exists a finite set
${\mathrm{I\!M}}_{dr}$
is compact, there exists a finite set
![]() ${\mathcal C}_N=\{c_{1},\cdots,c_{N}\}\subset {\mathrm{I\!M}}_{dr}\subset {\mathrm{I\!R}}^{dr}$
of centers of balls forming a minimal
${\mathcal C}_N=\{c_{1},\cdots,c_{N}\}\subset {\mathrm{I\!M}}_{dr}\subset {\mathrm{I\!R}}^{dr}$
of centers of balls forming a minimal
![]() $\epsilon$
-covering set for
$\epsilon$
-covering set for
![]() ${\mathrm{I\!M}}_{dr}$
, so that, for a fixed
${\mathrm{I\!M}}_{dr}$
, so that, for a fixed
![]() $x\in {\mathrm{I\!M}}_{dr}$
, there exists
$x\in {\mathrm{I\!M}}_{dr}$
, there exists
![]() $c_i \in {\mathcal C}_N\subset {\mathrm{I\!M}}_{dr}$
such that
$c_i \in {\mathcal C}_N\subset {\mathrm{I\!M}}_{dr}$
such that
Hence,
Consequently, for any
![]() $x\in {\mathrm{I\!M}}_{dr}$
,
$x\in {\mathrm{I\!M}}_{dr}$
,
and
Hence,
 \begin{eqnarray}&& \mathrm{I\!P}\!\left(\sup_{x\in {\mathrm{I\!M}}_{dr}}\min_{1\leq j\leq k}\|Y_{j,r}-x\| \geq 2\epsilon\right) \leq \mathrm{I\!P}\!\left( \max_{1\leq i\leq N}\min_{1\leq j\leq k}\|Y_{j,r}-c_i\| \geq \epsilon\right){\nonumber}\\[5pt] && \leq N \max_{1\leq i\leq N}\mathrm{I\!P}\!\left(\min_{1\leq j\leq k}\|Y_{j,r}-c_i\| \geq \epsilon\right)\leq N \sup_{x\in {\mathrm{I\!M}}_{dr}}\mathrm{I\!P}\!\left(\min_{1\leq j\leq k}\|Y_{j,r}-x\| \geq \epsilon\right).\end{eqnarray}
\begin{eqnarray}&& \mathrm{I\!P}\!\left(\sup_{x\in {\mathrm{I\!M}}_{dr}}\min_{1\leq j\leq k}\|Y_{j,r}-x\| \geq 2\epsilon\right) \leq \mathrm{I\!P}\!\left( \max_{1\leq i\leq N}\min_{1\leq j\leq k}\|Y_{j,r}-c_i\| \geq \epsilon\right){\nonumber}\\[5pt] && \leq N \max_{1\leq i\leq N}\mathrm{I\!P}\!\left(\min_{1\leq j\leq k}\|Y_{j,r}-c_i\| \geq \epsilon\right)\leq N \sup_{x\in {\mathrm{I\!M}}_{dr}}\mathrm{I\!P}\!\left(\min_{1\leq j\leq k}\|Y_{j,r}-x\| \geq \epsilon\right).\end{eqnarray}
We now have to bound N. For this we use [Reference Niyogi, Smale and Weinberger33, Lemma 5.2] (as was done in [Reference Fasy16]), to get
 \begin{equation}N\leq \left({\inf_{x\in \mathrm{I\!M}_{rd}}\mathrm{I\!P}(\|Y_{1,r} - x\| \leq \epsilon/2)}\right)^{-1}= \left(1-{\sup_{x\in \mathrm{I\!M}_{rd}}\mathrm{I\!P}(\|Y_{1,r}-x\|> \epsilon/2)}\right)^{-1}.\end{equation}
\begin{equation}N\leq \left({\inf_{x\in \mathrm{I\!M}_{rd}}\mathrm{I\!P}(\|Y_{1,r} - x\| \leq \epsilon/2)}\right)^{-1}= \left(1-{\sup_{x\in \mathrm{I\!M}_{rd}}\mathrm{I\!P}(\|Y_{1,r}-x\|> \epsilon/2)}\right)^{-1}.\end{equation}
Hence, by (3.2) together with (3.3) and (3.4),
 \begin{eqnarray}&& \mathrm{I\!P}\!\left(d_H({\mathbb Y}_{k} , {\mathrm{I\!M}}_{dr}) > 2\epsilon\right)\\[5pt] && \leq \left(1-{\sup_{x\in \mathrm{I\!M}_{rd}}\mathrm{I\!P}(\|Y_{1,r}-x\|> \epsilon/2)}\right)^{-1}\sup_{x\in \mathrm{I\!M}_{rd}}\mathrm{I\!P}\!\left(\min_{1\leq j\leq k}\|Y_{j,r}-x\| \geq \epsilon\right). {\nonumber}\end{eqnarray}
\begin{eqnarray}&& \mathrm{I\!P}\!\left(d_H({\mathbb Y}_{k} , {\mathrm{I\!M}}_{dr}) > 2\epsilon\right)\\[5pt] && \leq \left(1-{\sup_{x\in \mathrm{I\!M}_{rd}}\mathrm{I\!P}(\|Y_{1,r}-x\|> \epsilon/2)}\right)^{-1}\sup_{x\in \mathrm{I\!M}_{rd}}\mathrm{I\!P}\!\left(\min_{1\leq j\leq k}\|Y_{j,r}-x\| \geq \epsilon\right). {\nonumber}\end{eqnarray}
Thanks to (3.5), the proof of this proposition is complete if we prove that
Recall that
![]() $\mathrm{I\!P}({\mathbb X}_n \subset \mathrm{I\!M})=1$
, so that
$\mathrm{I\!P}({\mathbb X}_n \subset \mathrm{I\!M})=1$
, so that
![]() $ d_H({\mathbb X}_n , {\mathrm{I\!M}}) = \sup_{x\in \mathrm{I\!M}}\min_{1\leq j\leq n}\|X_j-x\|,$
and, since
$ d_H({\mathbb X}_n , {\mathrm{I\!M}}) = \sup_{x\in \mathrm{I\!M}}\min_{1\leq j\leq n}\|X_j-x\|,$
and, since
![]() $kr\leq n$
,
$kr\leq n$
,
From this we deduce that
It finally remains to prove that
For this, let
![]() $X_j\in {\mathbb X}_{kr} $
and
$X_j\in {\mathbb X}_{kr} $
and
![]() $x\in \mathrm{I\!M}$
. Then there exist l and i such that
$x\in \mathrm{I\!M}$
. Then there exist l and i such that
![]() $X_j$
is the lth component of the vector
$X_j$
is the lth component of the vector
![]() $Y_{i,r}$
. We claim also that there exists
$Y_{i,r}$
. We claim also that there exists
![]() ${\tilde x}\in \mathrm{I\!M}_{dr}$
such that x is the lth component of the vector
${\tilde x}\in \mathrm{I\!M}_{dr}$
such that x is the lth component of the vector
![]() ${\tilde x}$
. In fact, let
${\tilde x}$
. In fact, let
![]() $\pi_l\;:\; \mathrm{I\!R}^{dr}\rightarrow \mathrm{I\!R}^d$
be the projection onto the lth factor. It follows from an elementary property of the support, by the continuity of
$\pi_l\;:\; \mathrm{I\!R}^{dr}\rightarrow \mathrm{I\!R}^d$
be the projection onto the lth factor. It follows from an elementary property of the support, by the continuity of
![]() $\pi_l$
and the closure of
$\pi_l$
and the closure of
![]() ${\mathrm{I\!M}_{dr}}$
, that
${\mathrm{I\!M}_{dr}}$
, that
where
![]() $\overline{A}$
denotes, as before, the closure of the set A. So, in particular, any
$\overline{A}$
denotes, as before, the closure of the set A. So, in particular, any
![]() $x\in \mathrm{I\!M}$
is
$x\in \mathrm{I\!M}$
is
![]() $x=\pi_l({\tilde x})$
for some
$x=\pi_l({\tilde x})$
for some
![]() ${\tilde x} \in \mathrm{I\!M}_{dr}.$
From this, we deduce that, for any
${\tilde x} \in \mathrm{I\!M}_{dr}.$
From this, we deduce that, for any
![]() $X_j\in {\mathbb X}_{kr} $
and
$X_j\in {\mathbb X}_{kr} $
and
![]() $x\in \mathrm{I\!M}$
, there exist
$x\in \mathrm{I\!M}$
, there exist
![]() $1\leq i\leq k$
and
$1\leq i\leq k$
and
![]() ${\tilde x}\in \mathrm{I\!M}_{dr}$
such that, a.s.,
${\tilde x}\in \mathrm{I\!M}_{dr}$
such that, a.s.,
Hence,
Consequently, since
![]() $\mathrm{I\!P}({\mathbb X}_{kr} \subset \mathrm{I\!M})=1$
,
$\mathrm{I\!P}({\mathbb X}_{kr} \subset \mathrm{I\!M})=1$
,
From this we get (3.8). Now (3.8) together with (3.7) proves (3.6). The proof of the proposition is complete.
4. Asymptotically dense sequences of random variables
As indicated in the introduction, our main goal is to find conditions under which a sequence
![]() ${\mathbb X}$
is asymptotically dense in the common support (see Definition 1.1). In this section, we give conditions and several examples of dependent random variables for which this is the case. This property is established every time by means of Proposition 3.1 applied with suitable choices of subsequences k and r of n, and for all these examples, it holds that for any
${\mathbb X}$
is asymptotically dense in the common support (see Definition 1.1). In this section, we give conditions and several examples of dependent random variables for which this is the case. This property is established every time by means of Proposition 3.1 applied with suitable choices of subsequences k and r of n, and for all these examples, it holds that for any
![]() $\epsilon>0$
,
$\epsilon>0$
,
All proofs of the propositions listed in this section appear in Section 7.
.
4.0.1. Stationary m-dependent sequence on a compact set.
Recall that the sequence
![]() is m-dependent for some
is m-dependent for some
![]() $m\geq 0$
if the two
$m\geq 0$
if the two
![]() $\sigma$
-fields
$\sigma$
-fields
![]() $\sigma (X_i,\,\,i\leq k)$
and
$\sigma (X_i,\,\,i\leq k)$
and
![]() $\sigma (X_{i}, i\geq k+m+1)$
are independent for every k. In particular, 0-dependent is the same as independent.
$\sigma (X_{i}, i\geq k+m+1)$
are independent for every k. In particular, 0-dependent is the same as independent.
Example 4.1. (An m-dependent sequence.) Let
![]() $(T_i)_{i\in \mathrm{I\!N}}$
be a sequence of i.i.d. random variables with values in
$(T_i)_{i\in \mathrm{I\!N}}$
be a sequence of i.i.d. random variables with values in
![]() $\mathrm{I\!R}^d$
. Let h be a real-valued function defined on
$\mathrm{I\!R}^d$
. Let h be a real-valued function defined on
![]() ${\mathrm{I\!R}^{dm}}$
. The stationary sequence
${\mathrm{I\!R}^{dm}}$
. The stationary sequence
![]() $(X_n)_{n\in \mathrm{I\!N}}$
defined by
$(X_n)_{n\in \mathrm{I\!N}}$
defined by
![]() $X_n=h(T_n,T_{n+1},\cdots,T_{n+m})$
is a stationary sequence of m-dependent random variables.
$X_n=h(T_n,T_{n+1},\cdots,T_{n+m})$
is a stationary sequence of m-dependent random variables.
For
![]() $m\in \mathrm{I\!N}\setminus\{0\}$
,
$m\in \mathrm{I\!N}\setminus\{0\}$
,
![]() $\epsilon>0$
, and
$\epsilon>0$
, and
![]() $Y_{1,m}=(X_1,\cdots, X_m)^t$
, as in the introduction, define the concentration coefficient of the vector
$Y_{1,m}=(X_1,\cdots, X_m)^t$
, as in the introduction, define the concentration coefficient of the vector
![]() $Y_{1,m}$
by
$Y_{1,m}$
by
The following proposition gives conditions on
![]() $\rho_m(\epsilon)$
under which the asymptotically dense property evoked in Definition 1.1 is satisfied.
$\rho_m(\epsilon)$
under which the asymptotically dense property evoked in Definition 1.1 is satisfied.
Proposition 4.1. Let
![]() be a stationary sequence of m-dependent
be a stationary sequence of m-dependent
![]() $\mathrm{I\!R}^d$
-valued random vectors. Suppose that
$\mathrm{I\!R}^d$
-valued random vectors. Suppose that
![]() $X_1$
has compact support
$X_1$
has compact support
![]() $\mathrm{I\!M}$
. Let
$\mathrm{I\!M}$
. Let
![]() $\epsilon_0>0$
be fixed. Suppose that for any
$\epsilon_0>0$
be fixed. Suppose that for any
![]() $0<\epsilon<\epsilon_0$
, there exists a strictly positive constant
$0<\epsilon<\epsilon_0$
, there exists a strictly positive constant
![]() $\kappa_{\epsilon}$
such that
$\kappa_{\epsilon}$
such that
Then it holds for any
![]() $0<\epsilon<\epsilon_0$
and any
$0<\epsilon<\epsilon_0$
and any
![]() $n\geq m+1$
that
$n\geq m+1$
that
 \begin{eqnarray*}&&\mathrm{I\!P}\!\left(d_H({\mathbb X}_n , {\mathrm{I\!M}}) > \epsilon\right)\leq \frac{(1- \kappa_{\frac{\epsilon}{2}})^{[\frac{1}{2}[\frac{n}{m+1}]]}}{\kappa_{\frac{\epsilon}{4}}},\end{eqnarray*}
\begin{eqnarray*}&&\mathrm{I\!P}\!\left(d_H({\mathbb X}_n , {\mathrm{I\!M}}) > \epsilon\right)\leq \frac{(1- \kappa_{\frac{\epsilon}{2}})^{[\frac{1}{2}[\frac{n}{m+1}]]}}{\kappa_{\frac{\epsilon}{4}}},\end{eqnarray*}
where
![]() $[\cdot]$
denotes the integer part. Consequently, for any
$[\cdot]$
denotes the integer part. Consequently, for any
![]() $\alpha\in ]0,1[$
and any
$\alpha\in ]0,1[$
and any
![]() $n\geq n_0(\epsilon,\alpha)$
, where
$n\geq n_0(\epsilon,\alpha)$
, where
 \begin{align*}n_0(\epsilon,\alpha)= \frac{2(m+1)}{\kappa_{\frac{\epsilon}{2}}} \left(\log\left(\frac{1}{\alpha }\right)+ \log\left(\frac{1}{ \kappa_{\frac{\epsilon}{4}} } \right)\right)+ 3(m+1),\end{align*}
\begin{align*}n_0(\epsilon,\alpha)= \frac{2(m+1)}{\kappa_{\frac{\epsilon}{2}}} \left(\log\left(\frac{1}{\alpha }\right)+ \log\left(\frac{1}{ \kappa_{\frac{\epsilon}{4}} } \right)\right)+ 3(m+1),\end{align*}
we have
![]() $d_H({\mathbb X}_n , {\mathrm{I\!M}}) \leq \epsilon$
with probability at least
$d_H({\mathbb X}_n , {\mathrm{I\!M}}) \leq \epsilon$
with probability at least
![]() $1-\alpha$
.
$1-\alpha$
.
The requirements of Proposition 4.1 prove that the sequence
![]() is asymptotically dense in
is asymptotically dense in
![]() $\mathrm{I\!M}$
with threshold
$\mathrm{I\!M}$
with threshold
![]() $n_0(\epsilon,\alpha)$
as above.
$n_0(\epsilon,\alpha)$
as above.
4.0.2. Stationary m-approximable random variables on a compact set.
In this section we discuss, in the spirit of [Reference Hörmann and Kokoszka25], some examples of stationary compactly supported random variables
![]() $(X_n)_{n\in {\mathbb Z}}$
that can be approximated by m-dependent stationary sequences. More precisely, the article [Reference Hörmann and Kokoszka25] introduced the notion of an
$(X_n)_{n\in {\mathbb Z}}$
that can be approximated by m-dependent stationary sequences. More precisely, the article [Reference Hörmann and Kokoszka25] introduced the notion of an
![]() $L^p$
-m-approximable sequence. This notion is related to m-dependence (see [Reference Hörmann and Kokoszka25, Definition 2.1]) and is different from mixing (see Paragraph 4.0.3 below for a definition of mixing). The idea is to construct, for
$L^p$
-m-approximable sequence. This notion is related to m-dependence (see [Reference Hörmann and Kokoszka25, Definition 2.1]) and is different from mixing (see Paragraph 4.0.3 below for a definition of mixing). The idea is to construct, for
![]() $m\in \mathrm{I\!N}$
, a stationary sequence
$m\in \mathrm{I\!N}$
, a stationary sequence
![]() $(X_n^{(m)})_{n\in {\mathbb Z}}$
that is m-dependent and compactly supported, for which the Hausdorff distance between the two sets
$(X_n^{(m)})_{n\in {\mathbb Z}}$
that is m-dependent and compactly supported, for which the Hausdorff distance between the two sets
![]() ${{\mathbb X}}_n$
and
${{\mathbb X}}_n$
and
![]() ${{{\mathbb X}}_n^{(m)}}\;:\!=\;\{X_1^{(m)},\cdots, X_n^{(m)}\}$
is suitably controlled. In our case, it is not necessary that
${{{\mathbb X}}_n^{(m)}}\;:\!=\;\{X_1^{(m)},\cdots, X_n^{(m)}\}$
is suitably controlled. In our case, it is not necessary that
![]() $X_1$
and
$X_1$
and
![]() $X_1^{(m)}$
have the same distribution; rather, what we need is that
$X_1^{(m)}$
have the same distribution; rather, what we need is that
![]() $X_1$
and
$X_1$
and
![]() $X_1^{m}$
have the same compact support. This will give us more choices for the construction of the sequence
$X_1^{m}$
have the same compact support. This will give us more choices for the construction of the sequence
![]() $(X_n^{(m)})_{n\in {\mathbb Z}}$
, which can be obtained by the method of coupling or by a truncation argument (see [Reference Hörmann and Kokoszka25] for more details). For our purpose, we shall use a truncation.
$(X_n^{(m)})_{n\in {\mathbb Z}}$
, which can be obtained by the method of coupling or by a truncation argument (see [Reference Hörmann and Kokoszka25] for more details). For our purpose, we shall use a truncation.
More precisely, we will consider the sequence
where
![]() $(\epsilon_i)_{i\in {\mathbb Z}}$
is an i.i.d. sequence with values in some measurable space S and f is a real bounded function defined on
$(\epsilon_i)_{i\in {\mathbb Z}}$
is an i.i.d. sequence with values in some measurable space S and f is a real bounded function defined on
![]() $S^{\infty}$
. The sequence
$S^{\infty}$
. The sequence
![]() $(X_n^{(m)})_{n\in {\mathbb Z}}$
constructed from
$(X_n^{(m)})_{n\in {\mathbb Z}}$
constructed from
![]() $(X_n)_{n\in {\mathbb Z}}$
by truncation is
$(X_n)_{n\in {\mathbb Z}}$
by truncation is
Clearly
![]() $(X_n^{(m)})_{n\in {\mathbb Z}}$
is a stationary, m-dependent sequence and has the same compact support as
$(X_n^{(m)})_{n\in {\mathbb Z}}$
is a stationary, m-dependent sequence and has the same compact support as
![]() $(X_n)_{n\in {\mathbb Z}}$
as soon as f is bounded. We will thus assume that f is bounded; that is,
$(X_n)_{n\in {\mathbb Z}}$
as soon as f is bounded. We will thus assume that f is bounded; that is,
![]() $\|f\|_{\infty}=\sup_{x\in S^{\infty}}|f(x)|<\infty.$
As before,
$\|f\|_{\infty}=\sup_{x\in S^{\infty}}|f(x)|<\infty.$
As before,
![]() $\mathrm{I\!M}$
will be the common support of these two sequences.
$\mathrm{I\!M}$
will be the common support of these two sequences.
Now we need an additional assumption on f in order to ensure good control of the Hausdorff distance between the two sets
![]() ${{\mathbb X}}_n$
and
${{\mathbb X}}_n$
and
![]() ${{{\mathbb X}}_n^{(m)}}$
. We suppose that f is a real-valued bounded function and that it satisfies the following Lipschitz-type assumption (stated in [Reference Hörmann and Kokoszka25]): there exists a decreasing sequence
${{{\mathbb X}}_n^{(m)}}$
. We suppose that f is a real-valued bounded function and that it satisfies the following Lipschitz-type assumption (stated in [Reference Hörmann and Kokoszka25]): there exists a decreasing sequence
![]() $(c_m)_{m\in \mathrm{I\!N}}$
, tending to 0 as m tends to infinity, such that
$(c_m)_{m\in \mathrm{I\!N}}$
, tending to 0 as m tends to infinity, such that
for any numbers
![]() $a_l,x_i,y_i\in S$
,
$a_l,x_i,y_i\in S$
,
![]() $l\in\{1,m+1\}$
, and
$l\in\{1,m+1\}$
, and
![]() $ i\leq 0$
. This assumption is satisfied, for instance, by some autoregressive models.
$ i\leq 0$
. This assumption is satisfied, for instance, by some autoregressive models.
The next lemma proves that the truncated sequence
![]() $(X_n^{(m)})_{n\in {\mathbb Z}}$
is a Hausdorff approximation of the original sequence
$(X_n^{(m)})_{n\in {\mathbb Z}}$
is a Hausdorff approximation of the original sequence
![]() $(X_n)_{n\in {\mathbb Z}}$
.
$(X_n)_{n\in {\mathbb Z}}$
.
Lemma 4.1. Let
![]() $\epsilon>0$
be fixed, let
$\epsilon>0$
be fixed, let
![]() $(\epsilon_i)_{i\in {\mathbb Z}}$
be an i.i.d. sequence, let f be a bounded function satisfying (4.4), and let
$(\epsilon_i)_{i\in {\mathbb Z}}$
be an i.i.d. sequence, let f be a bounded function satisfying (4.4), and let
![]() $(X_n)_{n\in {\mathbb Z}}$
and
$(X_n)_{n\in {\mathbb Z}}$
and
![]() $(X_n^{(m)})_{n\in {\mathbb Z}}$
be the associated sequences as in (4.2) and (4.3), respectively. Let
$(X_n^{(m)})_{n\in {\mathbb Z}}$
be the associated sequences as in (4.2) and (4.3), respectively. Let
![]() $m \in \mathrm{I\!N}$
be such that
$m \in \mathrm{I\!N}$
be such that
where
![]() $\|f\|_{\infty}$
is the supremum of f. Then
$\|f\|_{\infty}$
is the supremum of f. Then
![]() $d_H({{\mathbb X}}^{(m)}_n, {{\mathbb X}}_n)<\epsilon$
, a.s.
$d_H({{\mathbb X}}^{(m)}_n, {{\mathbb X}}_n)<\epsilon$
, a.s.
In view of Lemma 4.1, the condition
![]() $\lim_{m\rightarrow \infty}c_m=0$
is enough to approximate, in the Hausdorff sense, the sequence
$\lim_{m\rightarrow \infty}c_m=0$
is enough to approximate, in the Hausdorff sense, the sequence
![]() $(X_n)_{n\in {\mathbb Z}}$
by the truncated sequence
$(X_n)_{n\in {\mathbb Z}}$
by the truncated sequence
![]() $(X_n^{(m)})_{n\in {\mathbb Z}}$
.
$(X_n^{(m)})_{n\in {\mathbb Z}}$
.
Proof. We recall that
Hence,
 \begin{eqnarray*} && \mathrm{I\!P}(d_H({{\mathbb X}}^{(m)}_n, {{\mathbb X}}_n)\geq \epsilon) \\[5pt] && \leq \mathrm{I\!P}(\max_{1\leq i\leq n}\min_{1\leq j\leq n}|X_i-X_j^{(m)}|\geq \epsilon) + \mathrm{I\!P}( \max_{1\leq i\leq n}\min_{1\leq j\leq n}|X_j-X_i^{(m)}|\geq \epsilon) \\[5pt] && \leq 2 n \max_{1\leq i \leq n}\mathrm{I\!P}( |X_i-X_i^{(m)}|\geq \epsilon).\end{eqnarray*}
\begin{eqnarray*} && \mathrm{I\!P}(d_H({{\mathbb X}}^{(m)}_n, {{\mathbb X}}_n)\geq \epsilon) \\[5pt] && \leq \mathrm{I\!P}(\max_{1\leq i\leq n}\min_{1\leq j\leq n}|X_i-X_j^{(m)}|\geq \epsilon) + \mathrm{I\!P}( \max_{1\leq i\leq n}\min_{1\leq j\leq n}|X_j-X_i^{(m)}|\geq \epsilon) \\[5pt] && \leq 2 n \max_{1\leq i \leq n}\mathrm{I\!P}( |X_i-X_i^{(m)}|\geq \epsilon).\end{eqnarray*}
Now,
Consequently, the event
![]() $( |X_i-X_i^{(m)}|\geq \epsilon)$
implies that
$( |X_i-X_i^{(m)}|\geq \epsilon)$
implies that
![]() $\epsilon \leq 2c_m \|f\|_{\infty}$
, and then the probability
$\epsilon \leq 2c_m \|f\|_{\infty}$
, and then the probability
![]() $\mathrm{I\!P}( |X_i-X_i^{(m)}|\geq \epsilon)$
vanishes whenever m satisfies
$\mathrm{I\!P}( |X_i-X_i^{(m)}|\geq \epsilon)$
vanishes whenever m satisfies
![]() $2c_m \|f\|_{\infty}<\epsilon$
. We conclude that, for such m,
$2c_m \|f\|_{\infty}<\epsilon$
. We conclude that, for such m,
![]() $\mathrm{I\!P}(d_H({{\mathbb X}}^{(m)}_n, {{\mathbb X}}_n)\geq \epsilon)=0$
.
$\mathrm{I\!P}(d_H({{\mathbb X}}^{(m)}_n, {{\mathbb X}}_n)\geq \epsilon)=0$
.
We can now apply Proposition 4.1 to the m-dependent sequence
![]() $(X_n^{(m)})_{n\in {\mathbb Z}}$
, combined with Lemma 4.1, to establish asymptotic
$(X_n^{(m)})_{n\in {\mathbb Z}}$
, combined with Lemma 4.1, to establish asymptotic
![]() $(\epsilon,\alpha)$
-density for
$(\epsilon,\alpha)$
-density for
![]() $(X_n)_{n\in{\mathbb Z}}$
. Doing this, we obtain the result below under a suitable control of the following concentration coefficient, related to the truncated sequence
$(X_n)_{n\in{\mathbb Z}}$
. Doing this, we obtain the result below under a suitable control of the following concentration coefficient, related to the truncated sequence
![]() $(X_n^{(m)})_{n\in {\mathbb Z}}$
(as defined in (4.3)):
$(X_n^{(m)})_{n\in {\mathbb Z}}$
(as defined in (4.3)):
with
![]() $Y_{1,m+1}^{(m)}=(X_1^{(m)},\cdots,X_{m+1}^{(m)})^t$
.
$Y_{1,m+1}^{(m)}=(X_1^{(m)},\cdots,X_{m+1}^{(m)})^t$
.
Proposition 4.2. Let
![]() $(X_n)_{n\in {\mathbb Z}}$
and f be as in the statement of Lemma 4.1. Let
$(X_n)_{n\in {\mathbb Z}}$
and f be as in the statement of Lemma 4.1. Let
![]() $\epsilon_0>0$
,
$\epsilon_0>0$
,
![]() $\epsilon \in ]0,\epsilon_0[$
be fixed, and let
$\epsilon \in ]0,\epsilon_0[$
be fixed, and let
![]() $m \in \mathrm{I\!N}$
be such that
$m \in \mathrm{I\!N}$
be such that
![]() $2c_m \|f\|_{\infty} < \epsilon$
. Suppose that the concentration coefficient
$2c_m \|f\|_{\infty} < \epsilon$
. Suppose that the concentration coefficient
![]() $\rho_{m+1}^{(m)}(\epsilon)$
related to the truncated sequence
$\rho_{m+1}^{(m)}(\epsilon)$
related to the truncated sequence
![]() $(X_n^{(m)})_{n\in {\mathbb Z}}$
, and defined in (4.5), satisfies
$(X_n^{(m)})_{n\in {\mathbb Z}}$
, and defined in (4.5), satisfies
for some
![]() ${\kappa_{\epsilon}}>0$
. Then for any
${\kappa_{\epsilon}}>0$
. Then for any
![]() $n\geq m+1$
,
$n\geq m+1$
,
 \begin{align*}\mathrm{I\!P}(d_H({\mathbb X}_n, \mathrm{I\!M})\geq 2\epsilon)\leq \frac{(1- \kappa_{\frac{\epsilon}{2}})^{[\frac{1}{2}[\frac{n}{m+1}]]}}{\kappa_{\frac{\epsilon}{4}}}, \end{align*}
\begin{align*}\mathrm{I\!P}(d_H({\mathbb X}_n, \mathrm{I\!M})\geq 2\epsilon)\leq \frac{(1- \kappa_{\frac{\epsilon}{2}})^{[\frac{1}{2}[\frac{n}{m+1}]]}}{\kappa_{\frac{\epsilon}{4}}}, \end{align*}
and a conclusion similar to that of Proposition 4.1 is true for such m.
Proof. This follows from Lemma 4.1 together with Proposition 4.1 and the fact that
 \begin{eqnarray*}&& \mathrm{I\!P}(d_H({\mathbb X}_n, \mathrm{I\!M})\geq 2\epsilon)\leq \mathrm{I\!P}(d_H({{\mathbb X}}_n, {\mathbb X}^{(m)}_n)+ d_H({{\mathbb X}}^{(m)}_n, \mathrm{I\!M}) \geq 2\epsilon) \\[5pt] &&\leq \mathrm{I\!P}(d_H({{\mathbb X}}_n, {{\mathbb X}}^{(m)}_n)\geq\epsilon)+ \mathrm{I\!P}(d_H({{\mathbb X}}^{(m)}_n, \mathrm{I\!M}) \geq\epsilon).\end{eqnarray*}
\begin{eqnarray*}&& \mathrm{I\!P}(d_H({\mathbb X}_n, \mathrm{I\!M})\geq 2\epsilon)\leq \mathrm{I\!P}(d_H({{\mathbb X}}_n, {\mathbb X}^{(m)}_n)+ d_H({{\mathbb X}}^{(m)}_n, \mathrm{I\!M}) \geq 2\epsilon) \\[5pt] &&\leq \mathrm{I\!P}(d_H({{\mathbb X}}_n, {{\mathbb X}}^{(m)}_n)\geq\epsilon)+ \mathrm{I\!P}(d_H({{\mathbb X}}^{(m)}_n, \mathrm{I\!M}) \geq\epsilon).\end{eqnarray*}
4.0.3. Stationary
 $\beta$
-mixing sequence on a compact set.
$\beta$
-mixing sequence on a compact set.
Recall that the stationary sequence
![]() $(X_n)_{n\in \mathrm{I\!N}}$
is
$(X_n)_{n\in \mathrm{I\!N}}$
is
![]() $\beta$
-mixing if
$\beta$
-mixing if
![]() $\beta_n$
tends to 0 when n tends to infinity, where the coefficients
$\beta_n$
tends to 0 when n tends to infinity, where the coefficients
![]() $(\beta_n)_{n>0}$
are defined as follows (see [Reference Bradley5, Reference Yu40] for the expression for
$(\beta_n)_{n>0}$
are defined as follows (see [Reference Bradley5, Reference Yu40] for the expression for
![]() $\beta_n$
):
$\beta_n$
):
The following corollary gives conditions on the behavior of the two sequences
![]() $(\rho_n(\epsilon))_{n>0}$
and
$(\rho_n(\epsilon))_{n>0}$
and
![]() $(\beta_n)_{n>0}$
under which the asymptotically dense property of Definition 1.1 is satisfied.
$(\beta_n)_{n>0}$
under which the asymptotically dense property of Definition 1.1 is satisfied.
Proposition 4.3. Let
![]() $(X_n)_{n\geq 0}$
be a stationary
$(X_n)_{n\geq 0}$
be a stationary
![]() $\beta$
-mixing sequence. Suppose that
$\beta$
-mixing sequence. Suppose that
![]() $X_1$
is supported on a compact set
$X_1$
is supported on a compact set
![]() $\mathrm{I\!M}$
. Then it holds, for any
$\mathrm{I\!M}$
. Then it holds, for any
![]() $\epsilon>0$
and any sequences
$\epsilon>0$
and any sequences
![]() $k_n$
and
$k_n$
and
![]() $r_n$
such that
$r_n$
such that
![]() $k_nr_n\leq n$
,
$k_nr_n\leq n$
,
 \begin{align*}\mathrm{I\!P}\!\left(d_H({\mathbb X}_n , {\mathrm{I\!M}}) > \epsilon\right) \leq\frac{k_n^2\beta_{r_n}+ k_n\exp\!\left(-[\frac{k_n}{2}]\rho_{r_n}(\epsilon/2)\right)}{k_n\rho_{r_n}(\epsilon/4)}.\end{align*}
\begin{align*}\mathrm{I\!P}\!\left(d_H({\mathbb X}_n , {\mathrm{I\!M}}) > \epsilon\right) \leq\frac{k_n^2\beta_{r_n}+ k_n\exp\!\left(-[\frac{k_n}{2}]\rho_{r_n}(\epsilon/2)\right)}{k_n\rho_{r_n}(\epsilon/4)}.\end{align*}
Suppose moreover that for some
![]() $\beta>1$
, and any
$\beta>1$
, and any
![]() $\epsilon>0$
small enough,
$\epsilon>0$
small enough,
Then
![]() $(X_n)_{n\geq 0}$
is asymptotically dense in
$(X_n)_{n\geq 0}$
is asymptotically dense in
![]() $\mathrm{I\!M}$
.
$\mathrm{I\!M}$
.
In the proof of Proposition 4.3 given in Section 7, we construct two sequences
![]() $(k_n)_n$
and
$(k_n)_n$
and
![]() $(r_n)_n$
for which
$(r_n)_n$
for which
 \begin{align*}\lim_{n\rightarrow \infty} \frac{k_n^2\beta_{r_n}+ k_n\exp\!\left(-[\frac{k_n}{2}]\rho_{r_n}(\epsilon/2)\right)}{k_n\rho_{r_n}(\epsilon/4)} =0.\end{align*}
\begin{align*}\lim_{n\rightarrow \infty} \frac{k_n^2\beta_{r_n}+ k_n\exp\!\left(-[\frac{k_n}{2}]\rho_{r_n}(\epsilon/2)\right)}{k_n\rho_{r_n}(\epsilon/4)} =0.\end{align*}
The threshold
![]() $n_0(\epsilon,\alpha)$
is not explicitly calculated, but it is that integer for which
$n_0(\epsilon,\alpha)$
is not explicitly calculated, but it is that integer for which
 \begin{align*} \frac{k_n^2\beta_{r_n}+ k_n\exp\!\left(-[\frac{k_n}{2}]\rho_{r_n}(\epsilon/2)\right)}{k_n\rho_{r_n}(\epsilon/4)} \leq \alpha,\end{align*}
\begin{align*} \frac{k_n^2\beta_{r_n}+ k_n\exp\!\left(-[\frac{k_n}{2}]\rho_{r_n}(\epsilon/2)\right)}{k_n\rho_{r_n}(\epsilon/4)} \leq \alpha,\end{align*}
for all
![]() $n\geq n_0(\epsilon,\alpha)$
.
$n\geq n_0(\epsilon,\alpha)$
.
4.0.4. Stationary weakly dependent sequence on a compact set.
We suppose here that
![]() is a stationary sequence such that
is a stationary sequence such that
![]() $X_1$
takes values in a compact support
$X_1$
takes values in a compact support
![]() $\mathrm{I\!M}$
. We suppose also that this sequence is weakly dependent in the sense of [Reference Doukhan and Louhichi14]. More precisely, we suppose that it satisfies the following definition.
$\mathrm{I\!M}$
. We suppose also that this sequence is weakly dependent in the sense of [Reference Doukhan and Louhichi14]. More precisely, we suppose that it satisfies the following definition.
Definition 4.1. We say that the sequence
![]() is
is
![]() $(\mathrm{I\!L}_{\infty}, \Psi)$
-weakly dependent if there exists a non-increasing function
$(\mathrm{I\!L}_{\infty}, \Psi)$
-weakly dependent if there exists a non-increasing function
![]() $\Psi$
such that
$\Psi$
such that
![]() $\lim_{r\rightarrow\infty}\Psi(r)=0$
, and such that for any measurable functions f and g bounded (respectively by
$\lim_{r\rightarrow\infty}\Psi(r)=0$
, and such that for any measurable functions f and g bounded (respectively by
![]() $\|f\|_{\infty}$
and
$\|f\|_{\infty}$
and
![]() $\|g\|_{\infty}$
) and for any
$\|g\|_{\infty}$
) and for any
![]() $ i_1\leq \cdots \leq i_k<i_{k}+r\leq i_{k+1}\leq \cdots\leq i_n$
one has
$ i_1\leq \cdots \leq i_k<i_{k}+r\leq i_{k+1}\leq \cdots\leq i_n$
one has
See [Reference Dedecker12, Definition 2.2] for a more general setting.
The dependence condition in Definition 4.1 is weaker than the Rosenblatt strong mixing dependence [Reference Rosenblatt35]. Let us briefly explain this. The
![]() $\alpha$
-mixing coefficient between the two sigma-fields
$\alpha$
-mixing coefficient between the two sigma-fields
![]() ${\mathcal A}$
and
${\mathcal A}$
and
![]() ${\mathcal B}$
is defined as
${\mathcal B}$
is defined as
The sequence
is strongly mixing if its coefficient
![]() $\alpha_n$
defined, for
$\alpha_n$
defined, for
![]() $n\geq 1$
, by
$n\geq 1$
, by
tends to 0 as n tends to infinity, with
![]() ${\mathcal P}_k=\sigma(X_i,\, i\leq k)$
and
${\mathcal P}_k=\sigma(X_i,\, i\leq k)$
and
![]() ${\mathcal F}_{k+n}=\sigma(X_i,\, i\geq k +n)$
. An equivalent formula for
${\mathcal F}_{k+n}=\sigma(X_i,\, i\geq k +n)$
. An equivalent formula for
![]() $\alpha_n$
, using the covariance between some functions, is stated in [Reference Bradley6, Theorem 4.4]:
$\alpha_n$
, using the covariance between some functions, is stated in [Reference Bradley6, Theorem 4.4]:
where
![]() $L_{\infty}({\mathcal A})$
denotes the set of bounded
$L_{\infty}({\mathcal A})$
denotes the set of bounded
![]() ${\mathcal A}$
-measurable functions for some
${\mathcal A}$
-measurable functions for some
![]() $\sigma$
-fields
$\sigma$
-fields
![]() $\mathcal A$
. It follows from this formula that strongly mixing sequences are
$\mathcal A$
. It follows from this formula that strongly mixing sequences are
![]() $(\mathrm{I\!L}_{\infty}, \Psi)$
-weakly dependent, as stated in Definition 4.1 (with
$(\mathrm{I\!L}_{\infty}, \Psi)$
-weakly dependent, as stated in Definition 4.1 (with
![]() $\Psi(r)=\alpha_r$
for
$\Psi(r)=\alpha_r$
for
![]() $r>0$
). The converse, however, is not necessarily true (see [Reference Dedecker12]).
$r>0$
). The converse, however, is not necessarily true (see [Reference Dedecker12]).
We can now state our result for stationary weakly dependent sequences.
Proposition 4.4. Let
![]() be a stationary,
be a stationary,
![]() $(\mathrm{I\!L}_{\infty}, \Psi)$
-weakly dependent sequence in the sense of Definition 4.1. Suppose that
$(\mathrm{I\!L}_{\infty}, \Psi)$
-weakly dependent sequence in the sense of Definition 4.1. Suppose that
![]() $X_1$
is supported on a compact set
$X_1$
is supported on a compact set
![]() $\mathrm{I\!M}$
. Then it holds, for any
$\mathrm{I\!M}$
. Then it holds, for any
![]() $\epsilon>0$
and any sequences
$\epsilon>0$
and any sequences
![]() $k_n$
and
$k_n$
and
![]() $r_n$
such that
$r_n$
such that
![]() $k_nr_n\leq n$
, that
$k_nr_n\leq n$
, that
 \begin{align*}\mathrm{I\!P}\!\left(d_H({\mathbb X}_n , {\mathrm{I\!M}}) > \epsilon\right) \leq\frac{k_n^2\Psi({r_n})+ k_n\exp\!\left(-[\frac{k_n}{2}]\rho_{r_n}(\epsilon/2)\right)}{k_n\rho_{r_n}(\epsilon/4)}.\end{align*}
\begin{align*}\mathrm{I\!P}\!\left(d_H({\mathbb X}_n , {\mathrm{I\!M}}) > \epsilon\right) \leq\frac{k_n^2\Psi({r_n})+ k_n\exp\!\left(-[\frac{k_n}{2}]\rho_{r_n}(\epsilon/2)\right)}{k_n\rho_{r_n}(\epsilon/4)}.\end{align*}
Suppose moreover that, for some
![]() $\beta>1$
, and any positive
$\beta>1$
, and any positive
![]() $\epsilon$
small enough,
$\epsilon$
small enough,
Then this sequence
![]() is asymptotically dense in
is asymptotically dense in
![]() $\mathrm{I\!M}$
.
$\mathrm{I\!M}$
.
Here again the threshold
![]() $n_0(\epsilon,\alpha)$
is not explicitly calculated but can be given by an inequality, as in the case of
$n_0(\epsilon,\alpha)$
is not explicitly calculated but can be given by an inequality, as in the case of
![]() $\beta$
-mixing.
$\beta$
-mixing.
4.1. Comparison with the i.i.d. case
We can compare the bounds of Proposition 4.1 (Propositions 4.3 and 4.4 respectively) with what has already been obtained in the i.i.d. case (see [Reference Chazal, Glisse, Labruyère and Michel7, Reference Cuevas10, Reference Cuevas and Rodrguez-Casal11]). That is, we restrict to the case when
![]() $m=0$
(respectively,
$m=0$
(respectively,
![]() $k_n=n$
and
$k_n=n$
and
![]() $r_n=1$
,
$r_n=1$
,
![]() $\beta_n=\Psi(n)=0$
for
$\beta_n=\Psi(n)=0$
for
![]() $n\geq 1$
). Suppose that we are in this situation and that, moreover,
$n\geq 1$
). Suppose that we are in this situation and that, moreover,
![]() $\rho_1(\epsilon)$
has a strictly positive lower bound, say
$\rho_1(\epsilon)$
has a strictly positive lower bound, say
![]() $\kappa_{\epsilon}$
. Then all the conclusions of the three propositions above give the same upper bound for
$\kappa_{\epsilon}$
. Then all the conclusions of the three propositions above give the same upper bound for
![]() $\mathrm{I\!P}\!\left(d_H({\mathbb X}_n , {\mathrm{I\!M}}) > \epsilon\right)$
, which is
$\mathrm{I\!P}\!\left(d_H({\mathbb X}_n , {\mathrm{I\!M}}) > \epsilon\right)$
, which is
Now we suppose, as already done in the i.i.d. case, that the (a, b)-standard assumption is satisfied, i.e,
![]() $\kappa_{\epsilon}= a \epsilon^{b},$
for some
$\kappa_{\epsilon}= a \epsilon^{b},$
for some
![]() $a>0$
,
$a>0$
,
![]() $b>0$
, and for positive
$b>0$
, and for positive
![]() $\epsilon$
small enough. Recall that the (a, b)-standard assumption was used, in the i.i.d. context, for set estimation problems under Hausdorff distance ([Reference Cuevas10, Reference Cuevas and Rodrguez-Casal11]) and also for a statistical analysis of persistence diagrams ([Reference Chazal, Glisse, Labruyère and Michel7, Reference Fasy16]). Then, clearly, an upper bound for (4.8) is
$\epsilon$
small enough. Recall that the (a, b)-standard assumption was used, in the i.i.d. context, for set estimation problems under Hausdorff distance ([Reference Cuevas10, Reference Cuevas and Rodrguez-Casal11]) and also for a statistical analysis of persistence diagrams ([Reference Chazal, Glisse, Labruyère and Michel7, Reference Fasy16]). Then, clearly, an upper bound for (4.8) is
for some positive constants C and c (independent of n and of
![]() $\epsilon$
), as has already been found in the i.i.d. case (see for instance the upper bound (3.2) in [Reference Cuevas10]). Finally, we have to check that the requirements of Propositions 4.1, 4.3, and 4.4 are satisfied under the (a, b)-standard assumption (i.e. when
$\epsilon$
), as has already been found in the i.i.d. case (see for instance the upper bound (3.2) in [Reference Cuevas10]). Finally, we have to check that the requirements of Propositions 4.1, 4.3, and 4.4 are satisfied under the (a, b)-standard assumption (i.e. when
![]() $\rho_1(\epsilon)\geq a \epsilon^{b}$
). Since we are in the case when
$\rho_1(\epsilon)\geq a \epsilon^{b}$
). Since we are in the case when
![]() $m=0$
in Proposition 4.1, and when
$m=0$
in Proposition 4.1, and when
![]() $\beta_n=0, \Psi_n=0, \, n\geq 1$
in Propositions 4.3 and 4.4, we have only to check that the (a, b)-standard assumption ensures, for i.i.d. random variables, that
$\beta_n=0, \Psi_n=0, \, n\geq 1$
in Propositions 4.3 and 4.4, we have only to check that the (a, b)-standard assumption ensures, for i.i.d. random variables, that
![]() $\lim_{m\rightarrow \infty} \rho_m(\epsilon)\frac{e^{m^{\beta}}}{m^{1+\beta}}=\infty$
. We deduce from the inequality
$\lim_{m\rightarrow \infty} \rho_m(\epsilon)\frac{e^{m^{\beta}}}{m^{1+\beta}}=\infty$
. We deduce from the inequality
that
Now,
Hence,
![]() $\rho_m(\epsilon)\geq \rho_1^m(\epsilon/{\sqrt{m}}).$
Combining this bound with the (a, b)-standard assumption, we get
$\rho_m(\epsilon)\geq \rho_1^m(\epsilon/{\sqrt{m}}).$
Combining this bound with the (a, b)-standard assumption, we get
The left term tends to infinity as n goes to infinity (since
![]() $\beta>1$
); hence
$\beta>1$
); hence
![]() $\displaystyle\lim_{m\rightarrow \infty} \rho_m(\epsilon)\frac{e^{m^{\beta}}}{m^{1+\beta}}=\infty$
.
$\displaystyle\lim_{m\rightarrow \infty} \rho_m(\epsilon)\frac{e^{m^{\beta}}}{m^{1+\beta}}=\infty$
.
As an important conclusion, the previous three propositions generalize the i.i.d. case well, even without the (a, b)-standard assumption.
5. Application to stationary Markov chains on a compact state space
This section gives conditions on stationary Markov chains on a compact state space that guarantee that they are asymptotically dense in this state space. Those conditions can be checked by studying the
![]() $\beta$
-mixing properties of the Markov chains and applying Proposition 4.3 above. However, in this section we choose to be even more precise, adopting specific models and carrying out explicit calculations.
$\beta$
-mixing properties of the Markov chains and applying Proposition 4.3 above. However, in this section we choose to be even more precise, adopting specific models and carrying out explicit calculations.
Let
![]() $(X_n)_{n\geq 0}$
be a homogeneous Markov chain satisfying the following two assumptions:
$(X_n)_{n\geq 0}$
be a homogeneous Markov chain satisfying the following two assumptions:
-
(
 ${\mathcal A}_1$
) The Markov chain has an invariant measure
${\mathcal A}_1$
) The Markov chain has an invariant measure
 $\mu$
with compact support
$\mu$
with compact support
 $\mathrm{I\!M}$
(and then the chain is stationary).
$\mathrm{I\!M}$
(and then the chain is stationary). -
(
 ${\mathcal A}_2$
) The transition probability kernel K, defined for
${\mathcal A}_2$
) The transition probability kernel K, defined for
 $x\in \mathrm{I\!M}$
by is absolutely continuous with respect to some measure
$x\in \mathrm{I\!M}$
by is absolutely continuous with respect to some measure \begin{align*} K(x,\cdot) = \mathrm{I\!P}(X_1\in \cdot |X_0=x), \end{align*}
\begin{align*} K(x,\cdot) = \mathrm{I\!P}(X_1\in \cdot |X_0=x), \end{align*}
 $\nu$
on
$\nu$
on
 $\mathrm{I\!M}$
; that is, there exist a positive measure
$\mathrm{I\!M}$
; that is, there exist a positive measure
 $\nu$
and a positive function k such that for any
$\nu$
and a positive function k such that for any
 $x\in \mathrm{I\!M}$
,
$x\in \mathrm{I\!M}$
,
 $ K(x,dy)=k(x,y)\nu(dy)$
. Moreover, for some
$ K(x,dy)=k(x,y)\nu(dy)$
. Moreover, for some
 $b>0$
and
$b>0$
and
 $\epsilon_0>0$
, and there exists a positive constant
$\epsilon_0>0$
, and there exists a positive constant \begin{align*} V_{d}\;:\!=\;\inf_{x\in \mathrm{I\!M}}\inf_{0<\epsilon<\epsilon_0}\left(\frac{1}{\epsilon^b}\int_{B(x,\epsilon)\cap \mathrm{I\!M} }\nu(dx_1)\right)>0 \end{align*}
\begin{align*} V_{d}\;:\!=\;\inf_{x\in \mathrm{I\!M}}\inf_{0<\epsilon<\epsilon_0}\left(\frac{1}{\epsilon^b}\int_{B(x,\epsilon)\cap \mathrm{I\!M} }\nu(dx_1)\right)>0 \end{align*}
 $\kappa$
such that
$\kappa$
such that
 $\displaystyle \inf_{x\in \mathrm{I\!M},\,y\in \mathrm{I\!M}}k(x,y)\geq \kappa>0. $
$\displaystyle \inf_{x\in \mathrm{I\!M},\,y\in \mathrm{I\!M}}k(x,y)\geq \kappa>0. $
Proposition 5.1. Suppose that Assumptions
![]() $({\mathcal A}_1)$
and
$({\mathcal A}_1)$
and
![]() $({\mathcal A}_2)$
are satisfied for some Markov chain
$({\mathcal A}_2)$
are satisfied for some Markov chain
![]() $(X_n)_{n\geq 0}$
. Then, for any
$(X_n)_{n\geq 0}$
. Then, for any
![]() $n\geq 1$
and any positive
$n\geq 1$
and any positive
![]() $\epsilon$
small enough,
$\epsilon$
small enough,
Consequently this Markov chain is asymptotically dense in
![]() $\mathrm{I\!M}$
, with a threshold
$\mathrm{I\!M}$
, with a threshold
![]() $n_0(\epsilon,\alpha)$
given by
$n_0(\epsilon,\alpha)$
given by
and
![]() $V_d$
is as introduced in Assumption
$V_d$
is as introduced in Assumption
![]() $({\mathcal A}_2)$
.
$({\mathcal A}_2)$
.
The proof and some key lemmas are deferred to Section 7.4.
We next give examples of Markov chains satisfying the requirements of Proposition 5.1. These examples concern stationary Markov chains on balls and stationary Markov chains on circles.
5.1. Stationary Markov chains on a ball of
 $\mathrm{I\!R}^d$
$\mathrm{I\!R}^d$
5.1.1. Random difference equations.
Let
![]() $(X_n)_{n\geq 0}$
be a Markov chain defined, for
$(X_n)_{n\geq 0}$
be a Markov chain defined, for
![]() $n\geq 0$
, by
$n\geq 0$
, by
where
![]() $A_{n+1}$
is a
$A_{n+1}$
is a
![]() $(d\times d)$
-matrix,
$(d\times d)$
-matrix,
![]() $X_n\in \mathrm{I\!R}^d,\,\, B_n\in \mathrm{I\!R}^d$
, and
$X_n\in \mathrm{I\!R}^d,\,\, B_n\in \mathrm{I\!R}^d$
, and
![]() $(A_n,B_n)_{n\geq 1}$
is an i.i.d. sequence independent of
$(A_n,B_n)_{n\geq 1}$
is an i.i.d. sequence independent of
![]() $X_0$
. Recall that for a matrix M,
$X_0$
. Recall that for a matrix M,
![]() $\|M\|$
is the operator norm, defined by
$\|M\|$
is the operator norm, defined by
![]() $\|M\|=\sup_{x\in \mathrm{I\!R}^d,\,\|x\|=1}\|Mx\|$
. It is well known that for any
$\|M\|=\sup_{x\in \mathrm{I\!R}^d,\,\|x\|=1}\|Mx\|$
. It is well known that for any
![]() $n\geq 1$
,
$n\geq 1$
,
![]() $X_n$
is distributed as
$X_n$
is distributed as
![]() $\sum_{k=1}^n A_1\cdots A_{k-1}B_k + A_1\cdots A_{n}X_0$
; see for instance [Reference Kesten27]. It is also well known that the conditions (see [Reference Goldie and Maller21, Reference Kesten28])
$\sum_{k=1}^n A_1\cdots A_{k-1}B_k + A_1\cdots A_{n}X_0$
; see for instance [Reference Kesten27]. It is also well known that the conditions (see [Reference Goldie and Maller21, Reference Kesten28])
ensure the existence of a stationary solution to (5.1), and that
![]() $\|A_1\cdots A_n\|$
approaches 0 exponentially fast. If in addition
$\|A_1\cdots A_n\|$
approaches 0 exponentially fast. If in addition
![]() $\mathrm{I\!E}\|B_1\|^{\beta}<\infty$
for some
$\mathrm{I\!E}\|B_1\|^{\beta}<\infty$
for some
![]() $\beta>0$
, then the series
$\beta>0$
, then the series
![]() $R\;:\!=\;\sum_{i=1}^{\infty}A_1\cdots A_{i-1}B_i$
converges a.s. and the distribution of
$R\;:\!=\;\sum_{i=1}^{\infty}A_1\cdots A_{i-1}B_i$
converges a.s. and the distribution of
![]() $X_n$
converges to that of R, independently of
$X_n$
converges to that of R, independently of
![]() $X_0$
. The distribution of R is then that of the stationary measure of the chain.
$X_0$
. The distribution of R is then that of the stationary measure of the chain.
Compact state space. If
![]() $\|B_1\|\leq c<\infty$
for some fixed c, then this stationary Markov chain is
$\|B_1\|\leq c<\infty$
for some fixed c, then this stationary Markov chain is
![]() $\mathrm{I\!M}$
-compactly supported. In particular, if
$\mathrm{I\!M}$
-compactly supported. In particular, if
![]() $\|A_1\|\leq \rho <1$
for some fixed
$\|A_1\|\leq \rho <1$
for some fixed
![]() $\rho$
, then
$\rho$
, then
![]() $\mathrm{I\!M}$
is included in the ball
$\mathrm{I\!M}$
is included in the ball
![]() $B_d(0, \frac{c}{1-\rho})$
of
$B_d(0, \frac{c}{1-\rho})$
of
![]() $\mathrm{I\!R}^d$
.
$\mathrm{I\!R}^d$
.
Transition kernel. Suppose that, for any
![]() $x \in \mathrm{I\!M}$
, the random vector
$x \in \mathrm{I\!M}$
, the random vector
![]() $A_1x+B_1$
has a density
$A_1x+B_1$
has a density
![]() $f_{A_1x+B_1}$
with respect to the Lebesgue measure (here
$f_{A_1x+B_1}$
with respect to the Lebesgue measure (here
![]() $\nu$
is the Lebesgue measure) satisfying
$\nu$
is the Lebesgue measure) satisfying
![]() $\inf_{x,\,\,y\in \mathrm{I\!M}}f_{A_1x+B_1}(y)\geq \kappa$
; then
$\inf_{x,\,\,y\in \mathrm{I\!M}}f_{A_1x+B_1}(y)\geq \kappa$
; then
![]() $k(x,y)= f_{A_1x+B_1}(y)\geq \kappa>0.$
$k(x,y)= f_{A_1x+B_1}(y)\geq \kappa>0.$
We collect all of the above results in the following corollary.
Corollary 5.1. Suppose that in the model (5.1), the conditions (5.2) are satisfied, and moreover
![]() $\|B_1\|\leq c<\infty$
. If the density of
$\|B_1\|\leq c<\infty$
. If the density of
![]() $A_1x+B_1$
, denoted by
$A_1x+B_1$
, denoted by
![]() $f_{A_1x+B_1}$
, satisfies
$f_{A_1x+B_1}$
, satisfies
![]() $\inf_{x,\,\,y\in \mathrm{I\!M}}f_{A_1x+B_1}(y)\geq \kappa>0$
for some positive
$\inf_{x,\,\,y\in \mathrm{I\!M}}f_{A_1x+B_1}(y)\geq \kappa>0$
for some positive
![]() $\kappa$
, then Assumptions (
$\kappa$
, then Assumptions (
![]() ${\mathcal A}_1$
) and (
${\mathcal A}_1$
) and (
![]() ${\mathcal A}_2$
) are satisfied with
${\mathcal A}_2$
) are satisfied with
![]() $b=d$
and
$b=d$
and
![]() $\nu$
the Lebesgue measure on
$\nu$
the Lebesgue measure on
![]() $\mathrm{I\!R}^d$
.
$\mathrm{I\!R}^d$
.
Example: the AR(1) process in
 $\mathrm{I\!R}$
.
$\mathrm{I\!R}$
.
We consider a particular case of the Markov chain as defined in (5.1) with
![]() $d=1$
, where, for each n,
$d=1$
, where, for each n,
![]() $A_n=\rho$
with
$A_n=\rho$
with
![]() $|\rho|<1$
. We obtain the standard first-order linear autoregressive process, i.e.,
$|\rho|<1$
. We obtain the standard first-order linear autoregressive process, i.e.,
We suppose that
 $B_1$
has a density function
$B_1$
has a density function
 $f_B$
supported on
$f_B$
supported on
 $[\!-c,c]$
for some
$[\!-c,c]$
for some
 $c>0$
with
$c>0$
with
 $\kappa\;:\!=\;\inf_{x\in [-c,c]}f_B(x)>0$
, and
$\kappa\;:\!=\;\inf_{x\in [-c,c]}f_B(x)>0$
, and $X_0 \in [\frac{-c}{1-|\rho|}, \frac{c}{1-|\rho|}]$
.
$X_0 \in [\frac{-c}{1-|\rho|}, \frac{c}{1-|\rho|}]$
.
This Markov chain evolves in a compact state space which is a subset of
![]() $ [\frac{-c}{1-|\rho|}, \frac{c}{1-|\rho|}]$
. Thanks to Corollary 5.1,
$ [\frac{-c}{1-|\rho|}, \frac{c}{1-|\rho|}]$
. Thanks to Corollary 5.1,
![]() $(X_n)_n$
admits a stationary measure
$(X_n)_n$
admits a stationary measure
![]() $\mu$
. We have, moreover,
$\mu$
. We have, moreover,
Assumptions (
![]() ${\mathcal A}_1$
) and (
${\mathcal A}_1$
) and (
![]() ${\mathcal A}_2$
) are then satisfied with
${\mathcal A}_2$
) are then satisfied with
![]() $b=1$
and
$b=1$
and
![]() $\nu$
the Lebesgue measure on
$\nu$
the Lebesgue measure on
![]() $\mathrm{I\!R}$
.
$\mathrm{I\!R}$
.
Example: the AR(k) process in
 $\mathrm{I\!R}$
.
$\mathrm{I\!R}$
.
The AR(k) process is defined by
where
![]() $\alpha_1,\cdots,\alpha_k \in \mathrm{I\!R}$
. Since this model can be written in the form of (5.1) with
$\alpha_1,\cdots,\alpha_k \in \mathrm{I\!R}$
. Since this model can be written in the form of (5.1) with
![]() $d=1$
,
$d=1$
,
 \begin{align*}X_n= (Y_n,Y_{n-1},\cdots,Y_{n-k+1})^t,\,\,\,\, B_n= (\epsilon_n,0,\cdots,0)^t,\,\,\, A_n=\left( \begin{array}{c@{\quad}c@{\quad}c} \alpha_1 & \cdots & \alpha_k \\[5pt] I_{k-1} & & 0 \\[5pt] \end{array} \right),\end{align*}
\begin{align*}X_n= (Y_n,Y_{n-1},\cdots,Y_{n-k+1})^t,\,\,\,\, B_n= (\epsilon_n,0,\cdots,0)^t,\,\,\, A_n=\left( \begin{array}{c@{\quad}c@{\quad}c} \alpha_1 & \cdots & \alpha_k \\[5pt] I_{k-1} & & 0 \\[5pt] \end{array} \right),\end{align*}
all of the above results for random difference equations apply under the corresponding assumptions. In particular, the process AR(2) is stationary as soon as
![]() $|\alpha_2|<1$
and
$|\alpha_2|<1$
and
![]() $\alpha_2+ |\alpha_1|<1$
.
$\alpha_2+ |\alpha_1|<1$
.
5.2. The Möbius Markov chain on the circle
Our aim is to give an example of a Markov chain on the unit circle, known as the Möbius Markov chain, which satisfies the requirements of Proposition 5.1. This Markov chain
![]() $(X_n)_{n\in \mathrm{I\!N}}$
is introduced in [Reference Kato26] and is defined as follows:
$(X_n)_{n\in \mathrm{I\!N}}$
is introduced in [Reference Kato26] and is defined as follows:
 $X_0$
is a random variable which takes values on the unit circle.
$X_0$
is a random variable which takes values on the unit circle.For
 $n\geq 1$
, where
$n\geq 1$
, where \begin{align*}X_n=\frac{X_{n-1} + \beta}{\beta X_{n-1}+1}\epsilon_n,\end{align*}
\begin{align*}X_n=\frac{X_{n-1} + \beta}{\beta X_{n-1}+1}\epsilon_n,\end{align*}
 $\beta\in ]-1,1[$
and
$\beta\in ]-1,1[$
and
 $(\epsilon_n)_{n\geq 1}$
is a sequence of i.i.d. random variables which are independent of
$(\epsilon_n)_{n\geq 1}$
is a sequence of i.i.d. random variables which are independent of
 $X_0$
and distributed as the wrapped Cauchy distribution with a common density with respect to the arc length measure
$X_0$
and distributed as the wrapped Cauchy distribution with a common density with respect to the arc length measure
 $\nu$
on the unit circle
$\nu$
on the unit circle
 $\partial B(0,1)$
,
$\partial B(0,1)$
,  \begin{align*}f_{\varphi}(z)= \frac{1}{2\pi}\frac{1-\varphi^2}{|z-\varphi|^2},\,\, \varphi\in [0,1[ \,\, {\mbox{fixed}},\,\,\, z\in \partial B(0,1).\end{align*}
\begin{align*}f_{\varphi}(z)= \frac{1}{2\pi}\frac{1-\varphi^2}{|z-\varphi|^2},\,\, \varphi\in [0,1[ \,\, {\mbox{fixed}},\,\,\, z\in \partial B(0,1).\end{align*}
The following proposition holds.
Proposition 5.2. Let
![]() $(X_n)_{n\geq 0}$
be the Möbius Markov chain on the unit circle as defined above. Then this Markov chain admits a unique invariant distribution, denoted by
$(X_n)_{n\geq 0}$
be the Möbius Markov chain on the unit circle as defined above. Then this Markov chain admits a unique invariant distribution, denoted by
![]() $\mu$
. If
$\mu$
. If
![]() $X_0$
is distributed as
$X_0$
is distributed as
![]() $\mu$
, then the set
$\mu$
, then the set
![]() ${\mathbb X}_n =\{X_1,\cdots,X_n\}$
converges in probability, as n tends to infinity, in the Hausdorff distance to the unit circle
${\mathbb X}_n =\{X_1,\cdots,X_n\}$
converges in probability, as n tends to infinity, in the Hausdorff distance to the unit circle
![]() $\partial B(0,1)$
; more precisely, for any
$\partial B(0,1)$
; more precisely, for any
![]() $\alpha\in ]0,1[$
, any positive
$\alpha\in ]0,1[$
, any positive
![]() $\epsilon$
sufficiently small, and any
$\epsilon$
sufficiently small, and any
![]() $n\geq \frac{2}{\kappa v \epsilon}\left(\ln(\frac{1}{\alpha})+\ln(\frac{4}{\epsilon\kappa v}) \right) $
, we have
$n\geq \frac{2}{\kappa v \epsilon}\left(\ln(\frac{1}{\alpha})+\ln(\frac{4}{\epsilon\kappa v}) \right) $
, we have
with probability at least
![]() $1-\alpha$
. Here v is a finite positive constant and
$1-\alpha$
. Here v is a finite positive constant and
![]() $\kappa= \frac{1}{2\pi}\frac{1-\varphi}{1+\varphi}.$
$\kappa= \frac{1}{2\pi}\frac{1-\varphi}{1+\varphi}.$
The Möbius Markov chain of Proposition 5.2 is then asymptotically dense in the unit circle with a threshold
![]() $n_0(\epsilon,\alpha)$
given by
$n_0(\epsilon,\alpha)$
given by
![]() $\kappa$
being as in the statement of the proposition, while the positive constant v is defined by (5.5) below.
$\kappa$
being as in the statement of the proposition, while the positive constant v is defined by (5.5) below.
Proof. We have to prove that all the requirements of Proposition 5.1 are satisfied. Our main reference for this proof is [Reference Kato26], where it is shown that this Markov chain has a unique invariant measure
![]() $\mu$
on the unit circle. This measure
$\mu$
on the unit circle. This measure
![]() $\mu$
has full support on
$\mu$
has full support on
![]() $\partial B(0,1)$
(so that Assumption
$\partial B(0,1)$
(so that Assumption
![]() $({\mathcal A}_1)$
is satisfied with
$({\mathcal A}_1)$
is satisfied with
![]() $\mathrm{I\!M}=\partial B(0,1)$
). The task now is to check Assumption
$\mathrm{I\!M}=\partial B(0,1)$
). The task now is to check Assumption
![]() $({\mathcal A}_2)$
. We have also, for
$({\mathcal A}_2)$
. We have also, for
![]() $x\in \partial B(0,1)$
,
$x\in \partial B(0,1)$
,
where
![]() $\nu$
is the arc length measure on the unit circle, and for
$\nu$
is the arc length measure on the unit circle, and for
![]() $x,z\in \partial B(0,1)$
,
$x,z\in \partial B(0,1)$
,
with
Since
![]() $\frac{x+\beta}{\beta x+ 1}\in \partial B(0,1)$
whenever
$\frac{x+\beta}{\beta x+ 1}\in \partial B(0,1)$
whenever
![]() $x\in \partial B(0,1)$
, we obtain
$x\in \partial B(0,1)$
, we obtain
![]() $\displaystyle|\phi_1(x)|^2= \varphi^2.$
Now, for
$\displaystyle|\phi_1(x)|^2= \varphi^2.$
Now, for
![]() $x,z\in \partial B(0,1)$
,
$x,z\in \partial B(0,1)$
,
Hence,
We now have to check that, for some
![]() $\epsilon_0>0$
,
$\epsilon_0>0$
,
For this let
![]() $u\in \partial B(0,1)$
, and define
$u\in \partial B(0,1)$
, and define
![]() $\displaystyle\overset{\frown}{AB} = \int_{\partial B(0,1) \cap B(u,\epsilon)}\nu(dx_1).$
$\displaystyle\overset{\frown}{AB} = \int_{\partial B(0,1) \cap B(u,\epsilon)}\nu(dx_1).$
We have
![]() $\|u-A\|=\|u-B\|=\epsilon$
(see Figure 3). Let
$\|u-A\|=\|u-B\|=\epsilon$
(see Figure 3). Let
![]() $\alpha = \widehat{AOB}$
; then on the one hand
$\alpha = \widehat{AOB}$
; then on the one hand
![]() $\overset{\frown}{AB}=\alpha$
. On the other hand, since the triangle OAu is isosceles, with an angle of
$\overset{\frown}{AB}=\alpha$
. On the other hand, since the triangle OAu is isosceles, with an angle of
![]() $\alpha/2$
in O, we have
$\alpha/2$
in O, we have
![]() $\epsilon = 2\sin (\alpha/4)$
. We thus obtain
$\epsilon = 2\sin (\alpha/4)$
. We thus obtain
From this, (5.5) is satisfied.

Figure 3. The ball
![]() $B(u,\epsilon)$
intersects the unit circle at two points A and B.
$B(u,\epsilon)$
intersects the unit circle at two points A and B.
Assumption
![]() $({\mathcal A}_2)$
is satisfied thanks to (5.3), (5.4), and (5.5). The proof of Proposition 5.2 is then complete by Proposition 5.1.
$({\mathcal A}_2)$
is satisfied thanks to (5.3), (5.4), and (5.5). The proof of Proposition 5.2 is then complete by Proposition 5.1.
6. Simulations
The purpose of this section is to simulate a Möbius Markov process on the unit circle (as defined in Section 5.2) and to illustrate the results of Proposition 5.2 and Theorem 2.2. More precisely, we simulate the following:
a random variable,
 $X_0$
, distributed as the uniform law on the unit circle
$X_0$
, distributed as the uniform law on the unit circle
 $\partial B(0,1)$
; that is,
$\partial B(0,1)$
; that is,
 $X_0$
has the density
$X_0$
has the density  \begin{align*}f(z) =\frac{1}{2\pi},\,\,\,\forall\,\, z\in \partial B(0,1);\end{align*}
\begin{align*}f(z) =\frac{1}{2\pi},\,\,\,\forall\,\, z\in \partial B(0,1);\end{align*}
for
 $n\geq 1$
,
$n\geq 1$
,
 $X_n=X_{n-1} \epsilon_n,$
, where
$X_n=X_{n-1} \epsilon_n,$
, where
 $(\epsilon_n)_{n\geq 1}$
is a sequence of i.i.d. random variables which are independent of
$(\epsilon_n)_{n\geq 1}$
is a sequence of i.i.d. random variables which are independent of
 $X_0$
and distributed as the wrapped Cauchy distribution with a common density, with respect to the arc length measure
$X_0$
and distributed as the wrapped Cauchy distribution with a common density, with respect to the arc length measure
 $\nu$
on the unit circle
$\nu$
on the unit circle
 $\partial B(0,1)$
, given by
$\partial B(0,1)$
, given by  \begin{align*}f_{\varphi}(z)= \frac{1}{2\pi}\frac{1-\varphi^2}{|z-\varphi|^2},\,\, \varphi\in [0,1[,\,\,\, z\in \partial B(0,1).\end{align*}
\begin{align*}f_{\varphi}(z)= \frac{1}{2\pi}\frac{1-\varphi^2}{|z-\varphi|^2},\,\, \varphi\in [0,1[,\,\,\, z\in \partial B(0,1).\end{align*}
In this case, it is proved in [Reference Kato26] that this Markov chain is stationary and its stationary measure is the uniform law on the unit circle.

Figure 4. Illustrations of the set
![]() $\{x_1,\cdots,x_{n}\}$
which is a realization of the stationary random variables
$\{x_1,\cdots,x_{n}\}$
which is a realization of the stationary random variables
![]() ${\mathbb X}_n = \{X_1,\ldots, X_n\}$
for different values of n and with
${\mathbb X}_n = \{X_1,\ldots, X_n\}$
for different values of n and with
![]() $\varphi=0$
.
$\varphi=0$
.

Figure 5. In the above images, the points of
![]() ${\mathbb X}_n$
are in red. Each of these points is the center of a circle with radius
${\mathbb X}_n$
are in red. Each of these points is the center of a circle with radius
![]() $r=0.1$
. This is an illustration of the reconstruction result
$r=0.1$
. This is an illustration of the reconstruction result
![]() $M \overset{\simeq}{\longrightarrow}\bigcup_{x\in{\mathbb X}_n}B(x,r)$
, with different values of n and with
$M \overset{\simeq}{\longrightarrow}\bigcup_{x\in{\mathbb X}_n}B(x,r)$
, with different values of n and with
![]() $r=0.1$
. In the above, there is reconstruction when
$r=0.1$
. In the above, there is reconstruction when
![]() $n=140$
and
$n=140$
and
![]() $r=0.1$
. The density
$r=0.1$
. The density
![]() $\frac{\epsilon}{2}$
is at least
$\frac{\epsilon}{2}$
is at least
![]() $\frac{2\pi}{280} = 0.0224$
, and so
$\frac{2\pi}{280} = 0.0224$
, and so
![]() $\epsilon$
is at least
$\epsilon$
is at least
![]() $0.0448$
. For this value of
$0.0448$
. For this value of
![]() $\epsilon=0.0448$
,
$\epsilon=0.0448$
,
![]() $\epsilon <r=0.1$
and this reconstruction is consistent with Theorem 2.2.
$\epsilon <r=0.1$
and this reconstruction is consistent with Theorem 2.2.
7. Deferred proofs
7.1. Proof of Proposition 4.1
Let
![]() $\epsilon_0>0$
and
$\epsilon_0>0$
and
![]() $\epsilon \in ]0,\epsilon_0[$
be fixed. In this proof we set
$\epsilon \in ]0,\epsilon_0[$
be fixed. In this proof we set
![]() $m'=m+1$
,
$m'=m+1$
,
![]() $r=m'$
, and
$r=m'$
, and
![]() $ k= k_n=[n/m']$
. Proposition 3.1, applied with these values of r and k, gives
$ k= k_n=[n/m']$
. Proposition 3.1, applied with these values of r and k, gives
 \begin{eqnarray}&&\mathrm{I\!P}\!\left(d_H({\mathbb X}_n , {\mathrm{I\!M}}) > \epsilon\right)\leq \mathrm{I\!P}\!\left(d_H(\{Y_{1,m'},\cdots,Y_{k_n,m'}\}, {\mathrm{I\!M}}_{dm'}) > \epsilon\right) {\nonumber} \\[5pt] && \leq \frac{\sup_{x\in {\mathrm{I\!M}}_{dm'}}\mathrm{I\!P}\!\left(\min_{1\leq i\leq k_n}\|Y_{i,m'}-x\|> \epsilon/2\right)}{1-\sup_{x\in {\mathrm{I\!M}}_{dm'}}\mathrm{I\!P}\!\left(\|Y_{1,m'}-x\|> \epsilon/4\right)},\end{eqnarray}
\begin{eqnarray}&&\mathrm{I\!P}\!\left(d_H({\mathbb X}_n , {\mathrm{I\!M}}) > \epsilon\right)\leq \mathrm{I\!P}\!\left(d_H(\{Y_{1,m'},\cdots,Y_{k_n,m'}\}, {\mathrm{I\!M}}_{dm'}) > \epsilon\right) {\nonumber} \\[5pt] && \leq \frac{\sup_{x\in {\mathrm{I\!M}}_{dm'}}\mathrm{I\!P}\!\left(\min_{1\leq i\leq k_n}\|Y_{i,m'}-x\|> \epsilon/2\right)}{1-\sup_{x\in {\mathrm{I\!M}}_{dm'}}\mathrm{I\!P}\!\left(\|Y_{1,m'}-x\|> \epsilon/4\right)},\end{eqnarray}
where
![]() $Y_{i,m'}= (X_{(i-1)m'+1},\cdots,X_{im'})^t.$
The sequence
$Y_{i,m'}= (X_{(i-1)m'+1},\cdots,X_{im'})^t.$
The sequence
![]() is stationary and assumed to be m-dependent. Consequently, the two families
is stationary and assumed to be m-dependent. Consequently, the two families
![]() $\{Y_{1,m'}, Y_{3,m'}, Y_{5,m'},\cdots\}$
and
$\{Y_{1,m'}, Y_{3,m'}, Y_{5,m'},\cdots\}$
and
![]() $\{Y_{2,m'}, Y_{4,m'}, Y_{6,m'},\cdots\}$
each consist of i.i.d. random vectors. Since we are assuming that
$\{Y_{2,m'}, Y_{4,m'}, Y_{6,m'},\cdots\}$
each consist of i.i.d. random vectors. Since we are assuming that
![]() $\rho_{m'}(\epsilon)\geq \kappa_{\epsilon}$
, we have
$\rho_{m'}(\epsilon)\geq \kappa_{\epsilon}$
, we have
 \begin{eqnarray}&&\sup_{x\in {\mathrm{I\!M}}_{dm'}}\mathrm{I\!P}\!\left(\min_{1\leq i\leq k_n}\|Y_{i,m'}-x\|> \frac{\epsilon}{2}\right)\leq \sup_{x\in {\mathrm{I\!M}}_{dm'}}\mathrm{I\!P}\!\left(\min_{1\leq 2i\leq k_n}\|Y_{2i,m'}-x\|> \frac{\epsilon}{2}\right) {\nonumber}\\[5pt] &&\leq \sup_{x\in {\mathrm{I\!M}}_{dm'}}\left(\mathrm{I\!P}\!\left(\|Y_{1,m'}-x\|> \frac{\epsilon}{2}\right)\right)^{[k_n/2]}\leq \left(1- \rho_{m'}(\frac{\epsilon}{2})\right)^{[k_n/2]}\leq \left(1- \kappa_{\frac{\epsilon}{2}}\right)^{[k_n/2]}\end{eqnarray}
\begin{eqnarray}&&\sup_{x\in {\mathrm{I\!M}}_{dm'}}\mathrm{I\!P}\!\left(\min_{1\leq i\leq k_n}\|Y_{i,m'}-x\|> \frac{\epsilon}{2}\right)\leq \sup_{x\in {\mathrm{I\!M}}_{dm'}}\mathrm{I\!P}\!\left(\min_{1\leq 2i\leq k_n}\|Y_{2i,m'}-x\|> \frac{\epsilon}{2}\right) {\nonumber}\\[5pt] &&\leq \sup_{x\in {\mathrm{I\!M}}_{dm'}}\left(\mathrm{I\!P}\!\left(\|Y_{1,m'}-x\|> \frac{\epsilon}{2}\right)\right)^{[k_n/2]}\leq \left(1- \rho_{m'}(\frac{\epsilon}{2})\right)^{[k_n/2]}\leq \left(1- \kappa_{\frac{\epsilon}{2}}\right)^{[k_n/2]}\end{eqnarray}
and
Collecting the bounds (7.1), (7.2), and (7.3), we find that for any
![]() $\epsilon>0$
,
$\epsilon>0$
,
 \begin{align*}\mathrm{I\!P}\!\left(d_H({\mathbb X}_n , {\mathrm{I\!M}}) > \epsilon\right) \leq \frac{\left(1- \kappa_{\frac{\epsilon}{2}}\right)^{[k_n/2]}}{\kappa_{\frac{\epsilon}{4}}} \leq \frac{\exp\!\left(-\kappa_{\frac{\epsilon}{2}}[k_n/2]\right)}{\kappa_{\frac{\epsilon}{4}}}.\end{align*}
\begin{align*}\mathrm{I\!P}\!\left(d_H({\mathbb X}_n , {\mathrm{I\!M}}) > \epsilon\right) \leq \frac{\left(1- \kappa_{\frac{\epsilon}{2}}\right)^{[k_n/2]}}{\kappa_{\frac{\epsilon}{4}}} \leq \frac{\exp\!\left(-\kappa_{\frac{\epsilon}{2}}[k_n/2]\right)}{\kappa_{\frac{\epsilon}{4}}}.\end{align*}
Let
![]() $\alpha \in ]0,1[$
be such that
$\alpha \in ]0,1[$
be such that
 $\displaystyle\frac{\exp\!\left(-\kappa_{\frac{\epsilon}{2}}[k_n/2]\right)}{\kappa_{\frac{\epsilon}{4}}} \leq \alpha,$
which is equivalent to
$\displaystyle\frac{\exp\!\left(-\kappa_{\frac{\epsilon}{2}}[k_n/2]\right)}{\kappa_{\frac{\epsilon}{4}}} \leq \alpha,$
which is equivalent to
 \begin{align*}[k_n/2] \geq \frac{1}{\kappa_{\frac{\epsilon}{2}}} \log\left(\frac{1}{\alpha \kappa_{\frac{\epsilon}{4}} }\right).\end{align*}
\begin{align*}[k_n/2] \geq \frac{1}{\kappa_{\frac{\epsilon}{2}}} \log\left(\frac{1}{\alpha \kappa_{\frac{\epsilon}{4}} }\right).\end{align*}
Then, for any
![]() $n\geq \frac{2m'}{\kappa_{\frac{\epsilon}{2}}} \log\left(\frac{1}{\alpha \kappa_{\frac{\epsilon}{4}} }\right)+3m'$
, we have
$n\geq \frac{2m'}{\kappa_{\frac{\epsilon}{2}}} \log\left(\frac{1}{\alpha \kappa_{\frac{\epsilon}{4}} }\right)+3m'$
, we have
 \begin{align*}[k_n/2]\geq k_n/2-1\geq \frac{n}{2m'}-3/2 \geq \frac{1}{\kappa_{\frac{\epsilon}{2}}} \log\left(\frac{1}{\alpha \kappa_{\frac{\epsilon}{4}} }\right),\end{align*}
\begin{align*}[k_n/2]\geq k_n/2-1\geq \frac{n}{2m'}-3/2 \geq \frac{1}{\kappa_{\frac{\epsilon}{2}}} \log\left(\frac{1}{\alpha \kappa_{\frac{\epsilon}{4}} }\right),\end{align*}
and therefore
![]() $\displaystyle\mathrm{I\!P}\!\left(d_H({\mathbb X}_n , {\mathrm{I\!M}}) > \epsilon\right) \leq \alpha.$
The proof of Proposition 4.1 is complete.
$\displaystyle\mathrm{I\!P}\!\left(d_H({\mathbb X}_n , {\mathrm{I\!M}}) > \epsilon\right) \leq \alpha.$
The proof of Proposition 4.1 is complete.
7.2. Proof of Proposition 4.3
We use the blocking method of [Reference Yu40] to transform the dependent
![]() $\beta$
-mixing sequence
$\beta$
-mixing sequence
![]() $(X_n)_{n\in \mathrm{I\!N}}$
into a sequence of nearly independent blocks. Let
$(X_n)_{n\in \mathrm{I\!N}}$
into a sequence of nearly independent blocks. Let
![]() $Z_{2i,{r_n}}=(\xi_j,\,\, j\in \{(2i-1){r_n}+1,\cdots, 2i{r_n}\})^t$
be a sequence of i.i.d. random vectors independent of the sequence
$Z_{2i,{r_n}}=(\xi_j,\,\, j\in \{(2i-1){r_n}+1,\cdots, 2i{r_n}\})^t$
be a sequence of i.i.d. random vectors independent of the sequence
![]() $(X_i)_{i\in \mathrm{I\!N}}$
such that, for any i,
$(X_i)_{i\in \mathrm{I\!N}}$
such that, for any i,
![]() $Z_{2i,{r_n}}$
is distributed as
$Z_{2i,{r_n}}$
is distributed as
![]() $Y_{2i,{r_n}}$
(which is distributed as
$Y_{2i,{r_n}}$
(which is distributed as
![]() $Y_{1,{r_n}}$
). Lemma 4.1 of [Reference Yu40] proves that the two vectors
$Y_{1,{r_n}}$
). Lemma 4.1 of [Reference Yu40] proves that the two vectors
![]() $(Z_{2i,{r_n}})_i$
and
$(Z_{2i,{r_n}})_i$
and
![]() $(Y_{2i,{r_n}})_i$
are related by the following relation:
$(Y_{2i,{r_n}})_i$
are related by the following relation:
which is true for any measurable function bounded by 1. We then have, using the last bound,
 \begin{eqnarray*}&&k_n\sup_{x\in {\mathrm{I\!M}}_{d{r_n}}}\mathrm{I\!P}\!\left(\min_{1\leq i\leq k_n}\|Y_{i,{r_n}}-x\|> \epsilon\right)\leq k_n\sup_{x\in {\mathrm{I\!M}}_{d{r_n}}}\mathrm{I\!P}\!\left(\min_{1\leq 2i\leq k_n}\|Y_{2i,{r_n}}-x\|> \epsilon\right) \\[5pt] && \leq k_n\sup_{x\in {\mathrm{I\!M}}_{d{r_n}}}\left|\mathrm{I\!P}\!\left(\min_{1\leq 2i\leq k_n}\|Y_{2i,{r_n}}-x\|> \epsilon\right)-\mathrm{I\!P}\!\left(\min_{1\leq 2i\leq k_n}\|Z_{2i,{r_n}}-x\|> \epsilon\right)\right|\\[5pt] && + k_n\sup_{x\in {\mathrm{I\!M}}_{d{r_n}}}\mathrm{I\!P}\!\left(\min_{1\leq 2i\leq k_n}\|Z_{2i,{r_n}}-x\|> \epsilon\right)\\[5pt] && \leq k_n^2\beta_{r_n}+ k_n\sup_{x\in {\mathrm{I\!M}}_{d{r_n}}}\mathrm{I\!P}\!\left(\min_{1\leq 2i\leq k_n}\|Z_{2i,{r_n}}-x\|> \epsilon\right)\\[5pt] && \leq k_n^2\beta_{r_n}+ k_n\sup_{x\in {\mathrm{I\!M}}_{d{r_n}}}\Bigl(\mathrm{I\!P}\!\left(\|Y_{1,{r_n}}-x\|> \epsilon\right)\Bigr)^{[k_n/2]}\\[5pt] && \leq k_n^2\beta_{r_n}+ k_n\Bigl(1-\rho_{r_n}(\epsilon)\Bigr)^{[k_n/2]}\\[5pt] && \leq k_n^2\beta_{r_n}+ k_n\exp\!\left(-[\frac{k_n}{2}]\rho_{r_n}(\epsilon)\right)\end{eqnarray*}
\begin{eqnarray*}&&k_n\sup_{x\in {\mathrm{I\!M}}_{d{r_n}}}\mathrm{I\!P}\!\left(\min_{1\leq i\leq k_n}\|Y_{i,{r_n}}-x\|> \epsilon\right)\leq k_n\sup_{x\in {\mathrm{I\!M}}_{d{r_n}}}\mathrm{I\!P}\!\left(\min_{1\leq 2i\leq k_n}\|Y_{2i,{r_n}}-x\|> \epsilon\right) \\[5pt] && \leq k_n\sup_{x\in {\mathrm{I\!M}}_{d{r_n}}}\left|\mathrm{I\!P}\!\left(\min_{1\leq 2i\leq k_n}\|Y_{2i,{r_n}}-x\|> \epsilon\right)-\mathrm{I\!P}\!\left(\min_{1\leq 2i\leq k_n}\|Z_{2i,{r_n}}-x\|> \epsilon\right)\right|\\[5pt] && + k_n\sup_{x\in {\mathrm{I\!M}}_{d{r_n}}}\mathrm{I\!P}\!\left(\min_{1\leq 2i\leq k_n}\|Z_{2i,{r_n}}-x\|> \epsilon\right)\\[5pt] && \leq k_n^2\beta_{r_n}+ k_n\sup_{x\in {\mathrm{I\!M}}_{d{r_n}}}\mathrm{I\!P}\!\left(\min_{1\leq 2i\leq k_n}\|Z_{2i,{r_n}}-x\|> \epsilon\right)\\[5pt] && \leq k_n^2\beta_{r_n}+ k_n\sup_{x\in {\mathrm{I\!M}}_{d{r_n}}}\Bigl(\mathrm{I\!P}\!\left(\|Y_{1,{r_n}}-x\|> \epsilon\right)\Bigr)^{[k_n/2]}\\[5pt] && \leq k_n^2\beta_{r_n}+ k_n\Bigl(1-\rho_{r_n}(\epsilon)\Bigr)^{[k_n/2]}\\[5pt] && \leq k_n^2\beta_{r_n}+ k_n\exp\!\left(-[\frac{k_n}{2}]\rho_{r_n}(\epsilon)\right)\end{eqnarray*}
and
Consequently, Proposition 3.1 gives
 \begin{eqnarray}\mathrm{I\!P}\!\left(d_H({\mathbb X}_n , {\mathrm{I\!M}}) > \epsilon\right) &\leq &\frac{\sup_{x\in {\mathrm{I\!M}}_{dr_n}}\mathrm{I\!P}\!\left(\min_{1\leq i\leq k_n}\|Y_{i,r_n}-x\|> \epsilon/2\right)}{1-\sup_{x\in {\mathrm{I\!M}}_{dr_n}}\mathrm{I\!P}\!\left(\|Y_{1,r_n}-x\|> \epsilon/4\right)} {\nonumber}\\[5pt] &\leq & \frac{k_n^2\beta_{r_n}+ k_n\exp\!\left(-[\frac{k_n}{2}]\rho_{r_n}(\epsilon/2)\right)}{k_n\rho_{r_n}(\epsilon/4)}.\end{eqnarray}
\begin{eqnarray}\mathrm{I\!P}\!\left(d_H({\mathbb X}_n , {\mathrm{I\!M}}) > \epsilon\right) &\leq &\frac{\sup_{x\in {\mathrm{I\!M}}_{dr_n}}\mathrm{I\!P}\!\left(\min_{1\leq i\leq k_n}\|Y_{i,r_n}-x\|> \epsilon/2\right)}{1-\sup_{x\in {\mathrm{I\!M}}_{dr_n}}\mathrm{I\!P}\!\left(\|Y_{1,r_n}-x\|> \epsilon/4\right)} {\nonumber}\\[5pt] &\leq & \frac{k_n^2\beta_{r_n}+ k_n\exp\!\left(-[\frac{k_n}{2}]\rho_{r_n}(\epsilon/2)\right)}{k_n\rho_{r_n}(\epsilon/4)}.\end{eqnarray}
We now have to construct two sequences
![]() $k_n$
and
$k_n$
and
![]() $r_n$
such that
$r_n$
such that
![]() $ k_nr_n \leq n$
and
$ k_nr_n \leq n$
and
We have supposed that
![]() $\lim_{m\rightarrow \infty} \rho_m(\epsilon)\frac{e^{m^{\beta}}}{m^{1+\beta}}=\infty$
for some
$\lim_{m\rightarrow \infty} \rho_m(\epsilon)\frac{e^{m^{\beta}}}{m^{1+\beta}}=\infty$
for some
![]() $\beta>1$
. Define
$\beta>1$
. Define
![]() $\gamma =1/\beta\in ]0,1[$
and
$\gamma =1/\beta\in ]0,1[$
and
Then, letting
![]() $m=r_n=[(\ln n)^{\gamma}]$
, we have
$m=r_n=[(\ln n)^{\gamma}]$
, we have
![]() $\displaystyle\lim_{n\rightarrow \infty} k_n \frac{\rho_{r_n}(\epsilon)}{\ln n}=\infty,$
and then (since
$\displaystyle\lim_{n\rightarrow \infty} k_n \frac{\rho_{r_n}(\epsilon)}{\ln n}=\infty,$
and then (since
![]() $k_n\leq n$
),
$k_n\leq n$
),
From the last limit we have that
![]() $\lim_{n\rightarrow\infty} k_n\rho_{r_n}(\epsilon)=\infty$
and that, for n large enough and for some
$\lim_{n\rightarrow\infty} k_n\rho_{r_n}(\epsilon)=\infty$
and that, for n large enough and for some
![]() $C>2$
,
$C>2$
,
![]() $\displaystyle k_n \frac{\rho_{r_n}(\epsilon)}{\ln(k_n)}\geq C$
, so that
$\displaystyle k_n \frac{\rho_{r_n}(\epsilon)}{\ln(k_n)}\geq C$
, so that
Consequently,
![]() $\displaystyle \lim_{n\rightarrow \infty}k_n\exp\!\left(-\frac{k_n}{2}\rho_{r_n}(\epsilon)\right)=0$
. Now we deduce from
$\displaystyle \lim_{n\rightarrow \infty}k_n\exp\!\left(-\frac{k_n}{2}\rho_{r_n}(\epsilon)\right)=0$
. Now we deduce from
![]() $\lim_{m\rightarrow\infty} \frac{e^{2m^{\beta}}}{m^2}\beta_m=0$
that (letting
$\lim_{m\rightarrow\infty} \frac{e^{2m^{\beta}}}{m^2}\beta_m=0$
that (letting
![]() $m=r_n=[(\ln n)^{\gamma}]$
)
$m=r_n=[(\ln n)^{\gamma}]$
)
The two sequences
![]() $k_n$
and
$k_n$
and
![]() $r_n$
so constructed satisfy (7.5), and for these sequences it holds that
$r_n$
so constructed satisfy (7.5), and for these sequences it holds that
 \begin{align*}\lim_{n\rightarrow \infty}\frac{k_n^2\beta_{r_n}+ k_n\exp\!\left(-\frac{k_n}{2}\rho_{r_n}(\epsilon/2)\right)}{k_n\rho_{r_n}(\epsilon/4)}=0.\end{align*}
\begin{align*}\lim_{n\rightarrow \infty}\frac{k_n^2\beta_{r_n}+ k_n\exp\!\left(-\frac{k_n}{2}\rho_{r_n}(\epsilon/2)\right)}{k_n\rho_{r_n}(\epsilon/4)}=0.\end{align*}
Hence for any
![]() $\alpha\in ]0,1[$
there exists an integer
$\alpha\in ]0,1[$
there exists an integer
![]() $n_0(\epsilon,\alpha)$
such that for any
$n_0(\epsilon,\alpha)$
such that for any
![]() $n\geq n_0(\epsilon,\alpha)$
,
$n\geq n_0(\epsilon,\alpha)$
,
 \begin{align*}\frac{k_n^2\beta_{r_n}+ k_n\exp\!\left(-\frac{k_n}{2}\rho_{r_n}(\epsilon/2)\right)}{k_n\rho_{r_n}(\epsilon/4)}\leq \alpha.\end{align*}
\begin{align*}\frac{k_n^2\beta_{r_n}+ k_n\exp\!\left(-\frac{k_n}{2}\rho_{r_n}(\epsilon/2)\right)}{k_n\rho_{r_n}(\epsilon/4)}\leq \alpha.\end{align*}
Combining this last inequality with that of (7.4) finishes the proof of Proposition 4.3.
7.3. Proof of Proposition 4.4
We have
 \begin{eqnarray}&&k_n\mathrm{I\!P}\!\left(\min_{1\leq i\leq k_n}\|Y_{i,{r_n}}-x\|> \epsilon\right)\leq k_n\mathrm{I\!P}\!\left(\min_{1\leq 2i\leq k_n}\|Y_{2i,{r_n}}-x\|> \epsilon\right){\nonumber}\\[5pt] && \leq k_n\left|\mathrm{I\!P}\!\left(\min_{1\leq 2i\leq k_n}\|Y_{2i,{r_n}}-x\|> \epsilon\right)-\prod_{i:\,1\leq 2i\leq k_n} \mathrm{I\!P}\!\left(\|Y_{2i,{r_n}}-x\|> \epsilon\right)\right| {\nonumber}\\[5pt] && + k_n\prod_{i:\,1\leq 2i\leq k_n} \mathrm{I\!P}\!\left(\|Y_{2i,{r_n}}-x\|> \epsilon\right).\end{eqnarray}
\begin{eqnarray}&&k_n\mathrm{I\!P}\!\left(\min_{1\leq i\leq k_n}\|Y_{i,{r_n}}-x\|> \epsilon\right)\leq k_n\mathrm{I\!P}\!\left(\min_{1\leq 2i\leq k_n}\|Y_{2i,{r_n}}-x\|> \epsilon\right){\nonumber}\\[5pt] && \leq k_n\left|\mathrm{I\!P}\!\left(\min_{1\leq 2i\leq k_n}\|Y_{2i,{r_n}}-x\|> \epsilon\right)-\prod_{i:\,1\leq 2i\leq k_n} \mathrm{I\!P}\!\left(\|Y_{2i,{r_n}}-x\|> \epsilon\right)\right| {\nonumber}\\[5pt] && + k_n\prod_{i:\,1\leq 2i\leq k_n} \mathrm{I\!P}\!\left(\|Y_{2i,{r_n}}-x\|> \epsilon\right).\end{eqnarray}
For s events
![]() $A_1,\cdots,A_s$
(with the convention that,
$A_1,\cdots,A_s$
(with the convention that,
![]() $\prod_{j=1}^{0}\mathrm{I\!P}(A_j)=1$
), we have
$\prod_{j=1}^{0}\mathrm{I\!P}(A_j)=1$
), we have

Hence,

Applying the last bound with
![]() $A_i= \left(\|Y_{2i,{r_n}}-x\|> \epsilon\right)$
and using (4.7), we get
$A_i= \left(\|Y_{2i,{r_n}}-x\|> \epsilon\right)$
and using (4.7), we get
and
 \begin{eqnarray}&& \left|\mathrm{I\!P}\!\left(\min_{1\leq 2i\leq k_n}\|Y_{2i,{r_n}}-x\|> \epsilon\right)-\prod_{i:\,1\leq 2i\leq k_n} \mathrm{I\!P}\!\left(\|Y_{2i,{r_n}}-x\|> \epsilon\right)\right| \leq k_n\Psi({r_n}).\end{eqnarray}
\begin{eqnarray}&& \left|\mathrm{I\!P}\!\left(\min_{1\leq 2i\leq k_n}\|Y_{2i,{r_n}}-x\|> \epsilon\right)-\prod_{i:\,1\leq 2i\leq k_n} \mathrm{I\!P}\!\left(\|Y_{2i,{r_n}}-x\|> \epsilon\right)\right| \leq k_n\Psi({r_n}).\end{eqnarray}
Combining (7.6) and (7.7), we deduce that
 \begin{eqnarray*}&&k_n\mathrm{I\!P}\!\left(\min_{1\leq i\leq k_n}\|Y_{i,{r_n}}-x\|> \epsilon\right)\leq k_n^2\Psi({r_n})+ k_n\Bigl(1-\rho_{r_n}(\epsilon)\Bigr)^{[k_n/2]}\\[5pt] &&\leq k_n^2\Psi({r_n})+ k_n\exp\Bigl(-[k_n/2]\rho_{r_n}(\epsilon)\Bigr).\end{eqnarray*}
\begin{eqnarray*}&&k_n\mathrm{I\!P}\!\left(\min_{1\leq i\leq k_n}\|Y_{i,{r_n}}-x\|> \epsilon\right)\leq k_n^2\Psi({r_n})+ k_n\Bigl(1-\rho_{r_n}(\epsilon)\Bigr)^{[k_n/2]}\\[5pt] &&\leq k_n^2\Psi({r_n})+ k_n\exp\Bigl(-[k_n/2]\rho_{r_n}(\epsilon)\Bigr).\end{eqnarray*}
Consequently, as for (7.4), we get
 \begin{align*}\mathrm{I\!P}\!\left(d_H({\mathbb X}_n , {\mathrm{I\!M}}) > \epsilon\right) \leq\frac{k_n^2\Psi({r_n})+ k_n\exp\!\left(-[\frac{k_n}{2}]\rho_{r_n}(\epsilon/2)\right)}{k_n\rho_{r_n}(\epsilon/4)}.\end{align*}
\begin{align*}\mathrm{I\!P}\!\left(d_H({\mathbb X}_n , {\mathrm{I\!M}}) > \epsilon\right) \leq\frac{k_n^2\Psi({r_n})+ k_n\exp\!\left(-[\frac{k_n}{2}]\rho_{r_n}(\epsilon/2)\right)}{k_n\rho_{r_n}(\epsilon/4)}.\end{align*}
We now have to construct two sequences
![]() $r_n$
and
$r_n$
and
![]() $k_n$
such that
$k_n$
such that
This last construction is possible as argued at the end of the proof of Proposition 4.3.
7.4. Lemmas for Section 5
To prove Proposition 5.1, we need the following two lemmas in order to check the conditions of Proposition 3.1 (with
![]() $r=1$
). Recall that
$r=1$
). Recall that
![]() $\mathrm{I\!P}_{x}$
(resp.
$\mathrm{I\!P}_{x}$
(resp.
![]() $\mathrm{I\!P}_{\mu}$
) denotes the probability when the initial condition
$\mathrm{I\!P}_{\mu}$
) denotes the probability when the initial condition
![]() $X_0=x$
(resp.
$X_0=x$
(resp.
![]() $X_0$
is distributed as the stationary measure
$X_0$
is distributed as the stationary measure
![]() $\mu$
).
$\mu$
).
Lemma 7.1. Let
![]() $(X_n)_{n\geq 0}$
be a Markov chain satisfying Assumptions
$(X_n)_{n\geq 0}$
be a Markov chain satisfying Assumptions
![]() $({\mathcal A}_1)$
and
$({\mathcal A}_1)$
and
![]() $({\mathcal A}_2)$
. Then, for any
$({\mathcal A}_2)$
. Then, for any
![]() $0<\epsilon<\epsilon_0$
and any
$0<\epsilon<\epsilon_0$
and any
![]() $x_0\in \mathrm{I\!M}$
, it holds that
$x_0\in \mathrm{I\!M}$
, it holds that
Proof. Using Assumption
![]() $({\mathcal A}_2)$
, we have
$({\mathcal A}_2)$
, we have
 \begin{eqnarray*}&& \mathrm{I\!P}_{x_0}\left(\|X_1-x\|\leq \epsilon\right)=\mathrm{I\!P}_{x_0}\left(X_1\in B(x,\epsilon)\cap \mathrm{I\!M}\right)= \int_{B(x,\epsilon) \cap \mathrm{I\!M}} K(x_0,dx_1)\\[5pt] && = \int_{B(x,\epsilon)\cap \mathrm{I\!M}} k(x_0,x_1)\nu(dx_1)\\[5pt] && \geq \kappa \int_{B(x,\epsilon)\cap \mathrm{I\!M} }\nu(dx_1)\geq \kappa \epsilon^b\inf_{0<\epsilon<\epsilon_0}\left(\frac{1}{\epsilon^b}\int_{B(x,\epsilon)\cap \mathrm{I\!M} }\nu(dx_1)\right)\geq \kappa \epsilon^b V_{d}.\end{eqnarray*}
\begin{eqnarray*}&& \mathrm{I\!P}_{x_0}\left(\|X_1-x\|\leq \epsilon\right)=\mathrm{I\!P}_{x_0}\left(X_1\in B(x,\epsilon)\cap \mathrm{I\!M}\right)= \int_{B(x,\epsilon) \cap \mathrm{I\!M}} K(x_0,dx_1)\\[5pt] && = \int_{B(x,\epsilon)\cap \mathrm{I\!M}} k(x_0,x_1)\nu(dx_1)\\[5pt] && \geq \kappa \int_{B(x,\epsilon)\cap \mathrm{I\!M} }\nu(dx_1)\geq \kappa \epsilon^b\inf_{0<\epsilon<\epsilon_0}\left(\frac{1}{\epsilon^b}\int_{B(x,\epsilon)\cap \mathrm{I\!M} }\nu(dx_1)\right)\geq \kappa \epsilon^b V_{d}.\end{eqnarray*}
The proof of Lemma 7.1 is then complete since
![]() $\mathrm{I\!P}_{\mu}\left(\|X_1-x\|\leq \epsilon\right)=\int \mathrm{I\!P}_{x_0}\left(\|X_1-x\|\leq \epsilon\right) d\mu(x_0)$
.
$\mathrm{I\!P}_{\mu}\left(\|X_1-x\|\leq \epsilon\right)=\int \mathrm{I\!P}_{x_0}\left(\|X_1-x\|\leq \epsilon\right) d\mu(x_0)$
.
Lemma 7.2. Let
![]() $(X_n)_{n\geq 0}$
be a Markov chain satisfying Assumptions
$(X_n)_{n\geq 0}$
be a Markov chain satisfying Assumptions
![]() $({\mathcal A}_1)$
and
$({\mathcal A}_1)$
and
![]() $({\mathcal A}_2)$
. Then, for any
$({\mathcal A}_2)$
. Then, for any
![]() $0<\epsilon<\epsilon_0$
and
$0<\epsilon<\epsilon_0$
and
![]() $k\in \mathrm{I\!N}\setminus\{0\}$
, it holds that
$k\in \mathrm{I\!N}\setminus\{0\}$
, it holds that
7.5. Proof of Proposition 5.1
Proposition 3.1 , applied with
![]() $r=r_n=1$
and
$r=r_n=1$
and
![]() $k=k_n=n$
, gives
$k=k_n=n$
, gives
with
![]() $Y_{i,r}= (X_{(i-1)r+1},\cdots,X_{ir})$
so that
$Y_{i,r}= (X_{(i-1)r+1},\cdots,X_{ir})$
so that
![]() $Y_{i,1}=X_i$
. Consequently, noting that
$Y_{i,1}=X_i$
. Consequently, noting that
![]() $\mathrm{I\!M}_d=\mathrm{I\!M}$
, we have
$\mathrm{I\!M}_d=\mathrm{I\!M}$
, we have
 \begin{eqnarray*}&& \sup_{x\in {\mathrm{I\!M}}}\mathrm{I\!P}_{\mu}\left(\min_{1\leq i\leq n}\|X_i-x\|> \epsilon\right) \leq (1-\kappa \epsilon^bV_{d})^{n}\leq \exp\!(\!-n\kappa \epsilon^bV_{d}), \\[5pt] && 1-\sup_{x\in {\mathrm{I\!M}}}\mathrm{I\!P}_{\mu}\left(\|X_1-x\|> \epsilon\right) \geq \kappa\epsilon^b V_{d}>0.\end{eqnarray*}
\begin{eqnarray*}&& \sup_{x\in {\mathrm{I\!M}}}\mathrm{I\!P}_{\mu}\left(\min_{1\leq i\leq n}\|X_i-x\|> \epsilon\right) \leq (1-\kappa \epsilon^bV_{d})^{n}\leq \exp\!(\!-n\kappa \epsilon^bV_{d}), \\[5pt] && 1-\sup_{x\in {\mathrm{I\!M}}}\mathrm{I\!P}_{\mu}\left(\|X_1-x\|> \epsilon\right) \geq \kappa\epsilon^b V_{d}>0.\end{eqnarray*}
Combining the three last bounds, we obtain
The proof of the proposition is then complete since
![]() $\displaystyle \alpha \geq \frac{4^b\exp\!(\!-n\kappa \epsilon^bV_{d}/2^b)}{\kappa\epsilon^b V_{d}}$
is equivalent to
$\displaystyle \alpha \geq \frac{4^b\exp\!(\!-n\kappa \epsilon^bV_{d}/2^b)}{\kappa\epsilon^b V_{d}}$
is equivalent to
Acknowledgements
We are very grateful to both referees for their insightful comments, and for suggesting many improvements. One of the referees made very thorough and relevant remarks on both the topological and probabilistic parts. The first author would like to thank Sebastian Scholtes for insightful discussions on the material of Section 2 and [Reference Scholtes36]. The second author is grateful to Sophie Lemaire for the present form of the proof of Lemma 7.2.
Funding information
The first author is supported by an SFRG grant from the American University of Sharjah (AUS, UAE). The second author is supported by the Université Grenoble Alpes, CNRS, LJK.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.