Given a three-valued definition of validity, which choice of three-valued truth tables for the connectives can ensure that the resulting logic coincides exactly with classical logic? We give an answer to this question for the five monotonic consequence relations 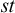 $st$,
$st$, 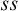 $ss$,
$ss$, 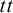 $tt$,
$tt$,  $ss\cap tt$, and
$ss\cap tt$, and 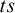 $ts$, when the connectives are negation, conjunction, and disjunction. For
$ts$, when the connectives are negation, conjunction, and disjunction. For 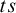 $ts$ and
$ts$ and  $ss\cap tt$ the answer is trivial (no scheme works), and for
$ss\cap tt$ the answer is trivial (no scheme works), and for 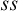 $ss$ and
$ss$ and 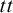 $tt$ it is straightforward (they are the collapsible schemes, in which the middle value acts like one of the classical values). For
$tt$ it is straightforward (they are the collapsible schemes, in which the middle value acts like one of the classical values). For 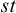 $st$, the schemes in question are the Boolean normal schemes that are either monotonic or collapsible.
$st$, the schemes in question are the Boolean normal schemes that are either monotonic or collapsible.