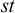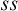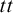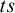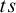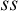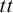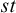1 Characterizing classical logic
Our goal in this paper is to provide a characterization of different ways in which classical logic can be presented in a three-valued setting. More precisely, our goal is to inventory which three-valued truth tables for negation, conjunction and disjunction can be paired with three-valued definitions of validity so as to yield exactly the same inferences that are obtained in more standard presentations of classical logic. While this project is mostly theoretical, it also has philosophical and conceptual motivations, about which we shall say more after stating the central results.
Toward our main goal, we first need to say more about the more standard ways in which classical logic has been characterized. Given a denumerable set of propositional variables
![]() $P=\{p, q, r, p', q', r',\ldots \}$
, a propositional logic is a triple
$P=\{p, q, r, p', q', r',\ldots \}$
, a propositional logic is a triple
![]() $\langle \mathcal {L}, C, \vdash \rangle $
such that C is a finite set of n-ary connectives,
$\langle \mathcal {L}, C, \vdash \rangle $
such that C is a finite set of n-ary connectives,
![]() $\mathcal {L}$
is the set of formulae generated from P by application of the connectives in C, and
$\mathcal {L}$
is the set of formulae generated from P by application of the connectives in C, and
![]() $\vdash $
is a relation between sets of formulae in
$\vdash $
is a relation between sets of formulae in
![]() $\mathcal {L}$
. In this paper, we will mainly focus on the set
$\mathcal {L}$
. In this paper, we will mainly focus on the set
![]() $C=\{\neg , \vee , \wedge \}$
, comprised of negation, disjunction and conjunction, forming a standard set of connectives in presentations of classical logic.
$C=\{\neg , \vee , \wedge \}$
, comprised of negation, disjunction and conjunction, forming a standard set of connectives in presentations of classical logic.
Given a propositional logic, what characterizes this logic as classical? One prominent answer to this question relies on two-valued semantics. On that view, a propositional logic is classical if the connectives are interpretable by specific two-valued truth functions, and
![]() $\vdash $
is interpretable by a specific relation between sets of truth values (where the values in question can be represented by
$\vdash $
is interpretable by a specific relation between sets of truth values (where the values in question can be represented by
![]() $1$
and
$1$
and
![]() $0$
, standing for True and False). Thus, for negation, conjunction, and disjunction to be classical, they must be interpretable by functions coextensional with
$0$
, standing for True and False). Thus, for negation, conjunction, and disjunction to be classical, they must be interpretable by functions coextensional with
![]() $f_{\neg }(x)=1-x, f_{\vee }(x,y)=max(x,y), f_{\wedge }(x,y)=min(x,y)$
on the set
$f_{\neg }(x)=1-x, f_{\vee }(x,y)=max(x,y), f_{\wedge }(x,y)=min(x,y)$
on the set
![]() $\mathcal {V}=\{1,0\}$
. Moreover,
$\mathcal {V}=\{1,0\}$
. Moreover,
![]() $\vdash $
is classical provided
$\vdash $
is classical provided
![]() $\Gamma \vdash \Delta $
if and only if for every valuation function v which is a homomorphism from
$\Gamma \vdash \Delta $
if and only if for every valuation function v which is a homomorphism from
![]() $(\mathcal {L},(\neg , \vee , \wedge ))$
to
$(\mathcal {L},(\neg , \vee , \wedge ))$
to
![]() $(\mathcal {V},(f_{\neg }, f_{\vee }, f_{\wedge }))$
,
$(\mathcal {V},(f_{\neg }, f_{\vee }, f_{\wedge }))$
,
![]() $\{v(A) : A\in \Gamma \}\subseteq \{1\}$
implies
$\{v(A) : A\in \Gamma \}\subseteq \{1\}$
implies
![]() $\{v(B) : B\in \Delta \}\cap \{1\}\neq \emptyset $
. That is, for every valuation, the truth of the premises in
$\{v(B) : B\in \Delta \}\cap \{1\}\neq \emptyset $
. That is, for every valuation, the truth of the premises in
![]() $\Gamma $
implies the truth of some conclusion in
$\Gamma $
implies the truth of some conclusion in
![]() $\Delta $
, which we can write
$\Delta $
, which we can write
![]() $\Gamma \vDash _2 \Delta $
.
$\Gamma \vDash _2 \Delta $
.
But what justifies the choice of these tables, and of this definition of validity? One possibility to answer this question is to look at syntax, namely proof-theory. Of particular interest to us is Gentzen’s perspective on the connectives and on the consequence relation. The leading idea behind Gentzen’s approach in his seminal work [Reference Gentzen21] is that what makes a logic classical is the fact that the connectives and the consequence relation obey specific rules. The way Gentzen described this is by specifying on the one hand structural rules governing the consequence relation
![]() $\vdash $
, and on the other operational rules governing the connectives. Arguably, this perspective is more explanatory than the semantic perspective, because it tells us how inferences are shaped to begin with.
$\vdash $
, and on the other operational rules governing the connectives. Arguably, this perspective is more explanatory than the semantic perspective, because it tells us how inferences are shaped to begin with.
As structural rules, Gentzen proposed various properties such as reflexivity, monotonicity, contraction, and the Cut rule (the rule allowing to infer
![]() $\Gamma, \Gamma' \vdash \Delta, \Delta'$
from
$\Gamma, \Gamma' \vdash \Delta, \Delta'$
from
![]() $\Gamma, A\vdash \Delta$
and
$\Gamma, A\vdash \Delta$
and
![]() $\Gamma' \vdash A, \Delta'$
). For operational rules Gentzen proposed analytic rules, telling us how an inference involving a connective in premise position or in conclusion position depends on other inferences not involving that connective but only involving subformulae. For negation, conjunction, and disjunction, the rules of his calculus
$\Gamma' \vdash A, \Delta'$
). For operational rules Gentzen proposed analytic rules, telling us how an inference involving a connective in premise position or in conclusion position depends on other inferences not involving that connective but only involving subformulae. For negation, conjunction, and disjunction, the rules of his calculus
![]() $\mathbf {LK}$
are displayed in Figure 1.
$\mathbf {LK}$
are displayed in Figure 1.
Does it matter whether one starts from a proof-theoretic or from a semantic characterization of classical logic? One may say that it does not, considering that the semantic and the syntactic perspective can be made to coincide. Gentzen’s sequent calculus
![]() $\mathbf {LK}$
, which characterizes
$\mathbf {LK}$
, which characterizes
![]() $\vdash $
syntactically, is sound and complete for the semantic interpretation
$\vdash $
syntactically, is sound and complete for the semantic interpretation
![]() $\vDash _2$
of the consequence relation between sets of formulae. However, Gentzen [Reference Gentzen21] has shown that Cut is eliminable from
$\vDash _2$
of the consequence relation between sets of formulae. However, Gentzen [Reference Gentzen21] has shown that Cut is eliminable from
![]() $\mathbf {LK}$
. In other words, the set of provable sequents in
$\mathbf {LK}$
. In other words, the set of provable sequents in
![]() $\mathbf {LK}$
minus Cut is the same as the set of provable sequents in
$\mathbf {LK}$
minus Cut is the same as the set of provable sequents in
![]() $\mathbf {LK}$
, i.e., exactly those that are classically valid. So, in the same way in which
$\mathbf {LK}$
, i.e., exactly those that are classically valid. So, in the same way in which
![]() $\mathbf {LK}$
minus Cut represents an alternative syntactic characterization of classical logic beside the one based on
$\mathbf {LK}$
minus Cut represents an alternative syntactic characterization of classical logic beside the one based on
![]() $\mathbf {LK}$
, one can also ask if there might be alternative semantic characterizations of classical logic beside the two-valued approach.
$\mathbf {LK}$
, one can also ask if there might be alternative semantic characterizations of classical logic beside the two-valued approach.

Figure 1 LK rules for negation (left), conjunction (middle), disjunction (right).
As it turns out, some authors have provided various three-valued semantics for classical logic. For instance, Girard in [Reference Girard22] offers a non-compositional semantics for
![]() $\mathbf {LK}$
minus Cut based on three-valued valuations (the so-called Schütte valuations), while Cobreros et al. [Reference Cobreros, Égré, Ripley and van Rooij8, Reference Cobreros, Égré, Ripley and van Rooij9] give a compositional semantics using the Strong Kleene valuations, and more recently, Szmuc and Ferguson [Reference Szmuc and Ferguson32] and Ferguson [Reference Ferguson14] show that the Weak Kleene valuations also work. All of these characterizations are given by the so-called
$\mathbf {LK}$
minus Cut based on three-valued valuations (the so-called Schütte valuations), while Cobreros et al. [Reference Cobreros, Égré, Ripley and van Rooij8, Reference Cobreros, Égré, Ripley and van Rooij9] give a compositional semantics using the Strong Kleene valuations, and more recently, Szmuc and Ferguson [Reference Szmuc and Ferguson32] and Ferguson [Reference Ferguson14] show that the Weak Kleene valuations also work. All of these characterizations are given by the so-called
![]() $st$
-consequence relation, defined by the fact that when all premises in
$st$
-consequence relation, defined by the fact that when all premises in
![]() $\Gamma $
take the value
$\Gamma $
take the value
![]() $1$
in the set
$1$
in the set
![]() , some conclusion in
, some conclusion in
![]() $\Delta $
takes a value other than
$\Delta $
takes a value other than
![]() $0$
(see [Reference Blasio, Marcos and Wansing2, Reference Frankowski19] for related discussions of this notion of consequence).
$0$
(see [Reference Blasio, Marcos and Wansing2, Reference Frankowski19] for related discussions of this notion of consequence).
In [Reference Chemla and Égré6], it is shown that beside
![]() $st$
, other consequence relations admit connectives satisfying Gentzen’s operational rules, and representable by means of three-valued operators. A case of interest is the non-reflexive relation
$st$
, other consequence relations admit connectives satisfying Gentzen’s operational rules, and representable by means of three-valued operators. A case of interest is the non-reflexive relation
![]() $ts$
, defined by the fact that when all premises in
$ts$
, defined by the fact that when all premises in
![]() $\Gamma $
take a value other than
$\Gamma $
take a value other than
![]() $0$
, some conclusion takes the value
$0$
, some conclusion takes the value
![]() $1$
(see [Reference French20, Reference Malinowski23, Reference Nicolai and Rossi25]). Thus, [Reference Chemla and Égré6] shows that when the language contains constants for the truth values,
$1$
(see [Reference French20, Reference Malinowski23, Reference Nicolai and Rossi25]). Thus, [Reference Chemla and Égré6] shows that when the language contains constants for the truth values,
![]() $ts$
admits as Gentzen-regular connectives the same Strong Kleene negation, conjunction and disjunction as
$ts$
admits as Gentzen-regular connectives the same Strong Kleene negation, conjunction and disjunction as
![]() $st$
. Similar results, both positive and negative, are obtained for alternative definitions of logical consequence, in particular for
$st$
. Similar results, both positive and negative, are obtained for alternative definitions of logical consequence, in particular for
![]() $ss$
(preservation of the value 1 from premises to conclusion), for
$ss$
(preservation of the value 1 from premises to conclusion), for
![]() $tt$
(preservation of non-falsity) and for their intersection
$tt$
(preservation of non-falsity) and for their intersection
![]() $ss\cap tt$
.Footnote
1
The theorems in [Reference Chemla and Égré6], however, do not purport to give a trivalent characterization of classical logic as defined above, namely in terms of both structural and operational rules (see section 4.1 for more on this). Instead, they focus only on operational rules, and for the most part they assume that the language can express all truth values, including the third value
$ss\cap tt$
.Footnote
1
The theorems in [Reference Chemla and Égré6], however, do not purport to give a trivalent characterization of classical logic as defined above, namely in terms of both structural and operational rules (see section 4.1 for more on this). Instead, they focus only on operational rules, and for the most part they assume that the language can express all truth values, including the third value
![]() .
.
In light of these results, we are led to the following question: what are all the three-valued schemes that can be used to characterize exactly those inferences valid in the two-valued presentation of classical logic, i.e.,
![]() $\vDash _2$
? To answer this question, we need to determine, for the five definitions of logical validity mentioned above (
$\vDash _2$
? To answer this question, we need to determine, for the five definitions of logical validity mentioned above (
![]() $st$
,
$st$
,
![]() $ss$
,
$ss$
,
![]() $tt$
,
$tt$
,
![]() $ss\cap tt$
, and
$ss\cap tt$
, and
![]() $ts$
), which three-valued truth tables can be assigned to negation, conjunction, and disjunction so as to yield all and only the inferences of the two-valued presentation of classical logic. For
$ts$
), which three-valued truth tables can be assigned to negation, conjunction, and disjunction so as to yield all and only the inferences of the two-valued presentation of classical logic. For
![]() $ts$
, the answer is trivial: no scheme will work, since
$ts$
, the answer is trivial: no scheme will work, since
![]() $p\vdash p$
fails in
$p\vdash p$
fails in
![]() $ts$
(see, e.g., [Reference Cobreros, Égré, Ripley and van Rooij8, Reference Malinowski23]). For the remaining four definitions of validity, the answer is less obvious, in particular in the case of
$ts$
(see, e.g., [Reference Cobreros, Égré, Ripley and van Rooij8, Reference Malinowski23]). For the remaining four definitions of validity, the answer is less obvious, in particular in the case of
![]() $st$
. For
$st$
. For
![]() $st$
, it is a contested matter whether it supports classical meta-inferences such as the Cut rule (see, e.g., [Reference Cobreros, Égré, Ripley and van Rooij8, Reference Dicher, Paoli, Başkent and Ferguson11]). However, here we are interested primarily in whether
$st$
, it is a contested matter whether it supports classical meta-inferences such as the Cut rule (see, e.g., [Reference Cobreros, Égré, Ripley and van Rooij8, Reference Dicher, Paoli, Başkent and Ferguson11]). However, here we are interested primarily in whether
![]() $st$
can support the same classical inferences as two-valued semantics.
$st$
can support the same classical inferences as two-valued semantics.
Our work proceeds as follows: in Section 2 we start by a review of three-valued definitions of validity, with an indication of the valuation schemes playing a central role in our results. Section 3 presents our main results, whose proof we defer to Appendix A to ease reading. Section 4 concludes with comparisons and a discussion of the philosophical value of those results.
2 Definitions
The question we are investigating in this paper may be put as follows: given a three-valued definition of logical consequence
![]() $\mathcal {C}$
, what set of truth tables
$\mathcal {C}$
, what set of truth tables
![]() $\mathbf {X}$
(or scheme) for the connectives can be such as to ensure that the resulting consequence relation
$\mathbf {X}$
(or scheme) for the connectives can be such as to ensure that the resulting consequence relation
![]() $\vDash ^{\mathcal {C}}_{\mathbf {X}}$
coincides with classical consequence? In this section we first introduce the five notions of validity of interest in a trivalent setting, where the truth values are 1,
$\vDash ^{\mathcal {C}}_{\mathbf {X}}$
coincides with classical consequence? In this section we first introduce the five notions of validity of interest in a trivalent setting, where the truth values are 1,
![]() , and 0. We then define the relevant properties of connectives and their truth tables, and give an overview of the way in which these properties constrain classicality for different consequence relations.
, and 0. We then define the relevant properties of connectives and their truth tables, and give an overview of the way in which these properties constrain classicality for different consequence relations.
2.1 Logical consequence
This section introduces five entailment relations corresponding to distinct ways of thinking of logical validity in a three-valued setting. They include the so-called pure, mixed, and intersective definitions of logical consequence, as defined in [Reference Chemla, Égré and Spector7].
Definition 2.1. Let a valuation be a function
![]() $v$
from formulae to the set
$v$
from formulae to the set
![]() .
.
-
(ss-validity)
 $\Gamma \vDash ^{ss}\Delta $
if and only if for every valuation
$\Gamma \vDash ^{ss}\Delta $
if and only if for every valuation
 $v$
, if
$v$
, if
 $v(A)= 1$
for every
$v(A)= 1$
for every
 $A \in \Gamma $
, then
$A \in \Gamma $
, then
 $v(B)= 1$
for some
$v(B)= 1$
for some
 $B \in \Delta $
.
$B \in \Delta $
. -
(tt-validity)
 $\Gamma \vDash ^{tt}\Delta $
if and only if for every valuation
$\Gamma \vDash ^{tt}\Delta $
if and only if for every valuation
 $v$
, if
$v$
, if
 for every
for every
 $A \in \Gamma $
, then
$A \in \Gamma $
, then
 for some
for some
 $B \in \Delta $
.
$B \in \Delta $
. -
(st-validity)
 $\Gamma \vDash ^{st}\Delta $
if and only if for every valuation
$\Gamma \vDash ^{st}\Delta $
if and only if for every valuation
 $v$
, if
$v$
, if
 $v(A)= 1$
for every
$v(A)= 1$
for every
 $A \in \Gamma $
, then
$A \in \Gamma $
, then
 for some
for some
 $B \in \Delta $
.
$B \in \Delta $
. -
(ts-validity)
 $\Gamma \vDash ^{ts}\Delta $
if and only if for every valuation
$\Gamma \vDash ^{ts}\Delta $
if and only if for every valuation
 $v$
, if
$v$
, if
 for every
for every
 $A \in \Gamma $
, then
$A \in \Gamma $
, then
 $v(B) = 1$
for some
$v(B) = 1$
for some
 $B \in \Delta $
.
$B \in \Delta $
. -
(ss ∩ tt-validity)
 $\Gamma \vDash ^{ss\cap tt}\Delta $
if and only if
$\Gamma \vDash ^{ss\cap tt}\Delta $
if and only if
 $\Gamma \vDash ^{ss}\Delta $
and
$\Gamma \vDash ^{ss}\Delta $
and
 $\Gamma \vDash ^{tt}\Delta $
; or equivalently, if and only if for every valuation
$\Gamma \vDash ^{tt}\Delta $
; or equivalently, if and only if for every valuation
 $v$
,
$v$
,
 $\inf \{v(A)|A \in \Gamma \} \leq _{\mathbb {Q}} \sup \{v(B)|B \in \Delta \}$
, where
$\inf \{v(A)|A \in \Gamma \} \leq _{\mathbb {Q}} \sup \{v(B)|B \in \Delta \}$
, where
 $\leq _{\mathbb {Q}}$
is the usual order over the rational numbers.
$\leq _{\mathbb {Q}}$
is the usual order over the rational numbers.
Basically, the pure notions of validity are the ones definable in terms of the preservation of a fixed set of designated values between premises and conclusions, they include
![]() $ss$
(preservation of value 1) and
$ss$
(preservation of value 1) and
![]() $tt$
(preservation of values that are not 0). The mixed notions of validity
$tt$
(preservation of values that are not 0). The mixed notions of validity
![]() $st$
and
$st$
and
![]() $ts$
define logical consequence not in terms of preservation but in terms of specific connections between values that can differ for premises and conclusions (not going from truth to falsity for
$ts$
define logical consequence not in terms of preservation but in terms of specific connections between values that can differ for premises and conclusions (not going from truth to falsity for
![]() $st$
, or from non-falsity to non-truth for
$st$
, or from non-falsity to non-truth for
![]() $ts$
). Finally, the intersective notion of validity
$ts$
). Finally, the intersective notion of validity
![]() $ss\cap tt$
has also been called order-theoretic in [Reference Chemla, Égré and Spector7, Reference Field15], because it is equivalent to requiring that, relative to the total ordering of truth-values
$ss\cap tt$
has also been called order-theoretic in [Reference Chemla, Égré and Spector7, Reference Field15], because it is equivalent to requiring that, relative to the total ordering of truth-values
![]() , the largest value of the conclusions should not be smaller than the smallest value of the premises.
, the largest value of the conclusions should not be smaller than the smallest value of the premises.
Although more entailment relations are conceivable, in [Reference Chemla, Égré and Spector7] these five were identified as the so-called intersective mixed consequence relations.Footnote
2
They form a natural class by corresponding to the three-valued monotonic consequence relations (namely such that if
![]() $\Gamma \vdash \Delta $
, then
$\Gamma \vdash \Delta $
, then
![]() $\Gamma ,\Gamma ' \vdash \Delta ,\Delta '$
). These consequence relations are related as depicted in Figure 2, in which a lower relation is an extensional subset of a higher relation.
$\Gamma ,\Gamma ' \vdash \Delta ,\Delta '$
). These consequence relations are related as depicted in Figure 2, in which a lower relation is an extensional subset of a higher relation.

Figure 2 The five intersective mixed consequence relations.
2.2 Schemes for the connectives: Boolean normal, monotonic, collapsible
We define a three-valued valuation scheme
![]() $\mathbf {X}$
as a triple
$\mathbf {X}$
as a triple
![]() $(f_{\neg }, f_{\wedge }, f_{\vee })$
of operations, namely of three-valued truth tables for the connectives. The properties of a scheme are defined in terms of the properties of its operations. Here we single out three main properties of interest: Boolean normality, monotonicity, and collapsibility.
$(f_{\neg }, f_{\wedge }, f_{\vee })$
of operations, namely of three-valued truth tables for the connectives. The properties of a scheme are defined in terms of the properties of its operations. Here we single out three main properties of interest: Boolean normality, monotonicity, and collapsibility.
We first define Boolean normal operations, that is operations that behave on Boolean values like their corresponding (“normal”) counterpart in classical logic. This property is also referred to in the literature as normality [Reference Priest28], or as regularity [Reference Priest, Égré and Rossi29]. For more on the origin of this terminology, going back to [Reference Post27, Reference Rescher30], see [Reference Teijeiro33] and references therein.Footnote 3
Definition 2.2 (Boolean normality)
An n-ary operation
![]() $\star $
is Boolean normal if and only if for
$\star $
is Boolean normal if and only if for
![]() $\{a_1,...,a_n\} \subseteq \{0,1\}$
,
$\{a_1,...,a_n\} \subseteq \{0,1\}$
,
![]() $\star (a_1,...,a_n)=\star ^{{\textsf{CL}}}(a_1,...,a_n)$
, where
$\star (a_1,...,a_n)=\star ^{{\textsf{CL}}}(a_1,...,a_n)$
, where
![]() $\star ^{{\textsf{CL}}}$
is the corresponding operation over the usual two-element Boolean algebra. A scheme is Boolean normal iff each of its operations is.
$\star ^{{\textsf{CL}}}$
is the corresponding operation over the usual two-element Boolean algebra. A scheme is Boolean normal iff each of its operations is.
Next, we assume that truth values are ordered with regard to
![]() $\leq _{\mathrm I}$
in terms of their so-called informational value, as described in [Reference Fitting16], that is,
$\leq _{\mathrm I}$
in terms of their so-called informational value, as described in [Reference Fitting16], that is,
![]() and
and
![]() , as depicted in Figure 3. Given such an ordering relation
, as depicted in Figure 3. Given such an ordering relation
![]() $<_{\mathrm I}$
, we can define the componentwise ordering based on this order as follows:
$<_{\mathrm I}$
, we can define the componentwise ordering based on this order as follows:
![]() $\langle a_1,...,a_n \rangle \leq _{\mathrm I}^{comp} \langle b_1,...,b_n \rangle $
if and only if
$\langle a_1,...,a_n \rangle \leq _{\mathrm I}^{comp} \langle b_1,...,b_n \rangle $
if and only if
![]() $a_j \leq _{\mathrm I} b_j$
for all
$a_j \leq _{\mathrm I} b_j$
for all
![]() $1 \leq _{\mathrm I} j \leq _{\mathrm I} k$
.
$1 \leq _{\mathrm I} j \leq _{\mathrm I} k$
.

Figure 3 Hasse diagram of the information order
![]() $\leq _{\mathrm I}$
.
$\leq _{\mathrm I}$
.
Definition 2.3 (Monotonicity)
An n-ary operation
![]() $\star $
is (upward) monotonic if and only if whenever
$\star $
is (upward) monotonic if and only if whenever
![]() $\langle a_1,...,a_n \rangle \leq _{\mathrm I}^{comp} \langle b_1,...,b_n \rangle $
then
$\langle a_1,...,a_n \rangle \leq _{\mathrm I}^{comp} \langle b_1,...,b_n \rangle $
then
![]() $\star (a_1,...,a_n) \leq _{\mathrm I} \star (b_1,...,b_n)$
. A scheme is monotonic if and only if each of its operations is.
$\star (a_1,...,a_n) \leq _{\mathrm I} \star (b_1,...,b_n)$
. A scheme is monotonic if and only if each of its operations is.
In 2D truth table format, monotonic operations are such that no two distinct classical values are found next to one another, horizontally or vertically. This is easy to prove and we refer to Appendix C for a tighter characterization.
By combining Boolean normality and monotonicity, we obtain the Boolean normal monotonic operations for negation, conjunction and disjunction presented in the truth tables in Figure 4. Here and elsewhere, when a cell contains more than one value, this means that any choice of a value renders an operation with the desired properties, independently of the choice of values in other cells (in this case, Boolean normality and monotonicity).

Figure 4 All the Boolean normal monotonic schemes.
To introduce our last relevant property, we define “
![]() $\alpha $
-collapsers,” operations
$\alpha $
-collapsers,” operations
![]() $\tau _{\alpha }$
defined as
$\tau _{\alpha }$
defined as
![]() $\tau _{\alpha }(0)=0$
,
$\tau _{\alpha }(0)=0$
,
![]() $\tau _{\alpha }(1)=1$
, and
$\tau _{\alpha }(1)=1$
, and
![]() , for
, for
![]() $\alpha =0$
or
$\alpha =0$
or
![]() $\alpha =1$
. As can be seen, collapsers preserve Boolean values, and collapse the third value onto
$\alpha =1$
. As can be seen, collapsers preserve Boolean values, and collapse the third value onto
![]() $\alpha $
.
$\alpha $
.
Definition 2.4 (Collapsibility)
An n-ary operation
![]() $\star $
is an
$\star $
is an
![]() $\alpha $
-collapsible version of a classical operation
$\alpha $
-collapsible version of a classical operation
![]() $\star ^{{\textsf{CL}}}$
iff
$\star ^{{\textsf{CL}}}$
iff
![]() $\tau _{\alpha }(\star (x_1, \dots , x_n)) = \star ^{{\textsf{CL}}}(\tau _{\alpha }(x_1), \dots , \tau _{\alpha }(x_n))$
. A scheme is
$\tau _{\alpha }(\star (x_1, \dots , x_n)) = \star ^{{\textsf{CL}}}(\tau _{\alpha }(x_1), \dots , \tau _{\alpha }(x_n))$
. A scheme is
![]() $\alpha $
-collapsible if and only if all of the operations are
$\alpha $
-collapsible if and only if all of the operations are
![]() $\alpha $
-collapsible.
$\alpha $
-collapsible.
In terms of truth tables, the
![]() $1$
-collapsible (henceforth, truth-collapsible) and the
$1$
-collapsible (henceforth, truth-collapsible) and the
![]() $0$
-collapsible (falsity-collapsible) operations are as reported in Figures 5 and 6, respectively.
$0$
-collapsible (falsity-collapsible) operations are as reported in Figures 5 and 6, respectively.

Figure 5 All the truth-collapsible schemes.

Figure 6 All the falsity-collapsible schemes.
We can see how these translate the definitions. First, the Boolean corners of the table should yield the same values as the corresponding Boolean operations, up to
![]() $\tau _{\alpha }$
. Second, in an area in which one can move by applying
$\tau _{\alpha }$
. Second, in an area in which one can move by applying
![]() $\tau _{\alpha }$
to one or both of the inputs, all output values should be the same, again up to
$\tau _{\alpha }$
to one or both of the inputs, all output values should be the same, again up to
![]() $\tau _{\alpha }$
. Therefore, the truth-collapsible scheme is one in which the values
$\tau _{\alpha }$
. Therefore, the truth-collapsible scheme is one in which the values
![]() $1$
and
$1$
and
![]() play the same functional role, whereas in the falsity-collapsible case the values
play the same functional role, whereas in the falsity-collapsible case the values
![]() $0$
and
$0$
and
![]() play the same role. Figures 7 and 8 display the Boolean normal collapsible operations.
play the same role. Figures 7 and 8 display the Boolean normal collapsible operations.

Figure 7 All the Boolean normal truth-collapsible schemes.

Figure 8 All the Boolean normal falsity-collapsible schemes.
Finally, notice that no collapsible negation is monotonic, because the third value yields a determinate value for collapsible negations, and an indeterminate for the monotonic negation. This implies that no collapsible scheme is monotonic, and conversely.
Various examples from the literature can be given to illustrate those schemes. The well-known Strong Kleene scheme and the Bochvar/Weak Kleene scheme are both Boolean normal monotonic schemes. Boolean normal monotonic schemes also include other schemes, such as the scheme characteristic of Lisp logic as discussed in Fitting’s [Reference Fitting16], first introduced by McCarthy in [Reference McCarthy24]—also to be found in the presupposition projection literature, in particular in Peters’ [Reference Peters26].Footnote
4
Likewise, the collapsible schemes are not just theoretical possibilities: an example of truth-collapsible scheme can be found in Cantwell’s [Reference Cantwell3], under the name “non-bivalent classical valuation.” Cantwell gives tables for negation, conjunction, and disjunction that are Boolean normal truth-collapsible. Additionally, he defines a conditional operator (originally introduced independently by Cooper in [Reference Cooper10]), which is not Boolean normal (it yields the value
![]() when the antecedent has value
when the antecedent has value
![]() $0$
, and takes the value of the consequent otherwise), but which could be shown to be truth-collapsible.Footnote
5
$0$
, and takes the value of the consequent otherwise), but which could be shown to be truth-collapsible.Footnote
5
2.3 Interaction of logical consequence and schemes: overview of the results
With the definition of logical consequence and of a valuation scheme in hand, we can restate our main goal more precisely as follows.
Definition 2.5. Given a scheme
![]() $\mathbf {X}$
and a definition of logical consequence
$\mathbf {X}$
and a definition of logical consequence
![]() $\mathcal {C}$
, we write
$\mathcal {C}$
, we write
![]() $\vDash _{\mathbf {X}}^{\mathcal {C}}$
the corresponding consequence relation, namely the set of valid arguments based on the scheme
$\vDash _{\mathbf {X}}^{\mathcal {C}}$
the corresponding consequence relation, namely the set of valid arguments based on the scheme
![]() $\mathbf {X}$
relying on the
$\mathbf {X}$
relying on the
![]() $\mathcal {C}$
definition of validity.
$\mathcal {C}$
definition of validity.
Our key question is: for a given definition of validity
![]() $\mathcal {C}$
, what scheme is inferentially classical? The relevant definition of inferential classicality is as follows:
$\mathcal {C}$
, what scheme is inferentially classical? The relevant definition of inferential classicality is as follows:
Definition 2.6. Given a scheme
![]() $\mathbf {X}$
and a definition of logical consequence
$\mathbf {X}$
and a definition of logical consequence
![]() $\mathcal {C}$
, we say
$\mathcal {C}$
, we say
![]() $\vDash _{\mathbf {X}}^{\mathcal {C}}$
is inferentially classical if and only if for every pair of sets of formulae
$\vDash _{\mathbf {X}}^{\mathcal {C}}$
is inferentially classical if and only if for every pair of sets of formulae
![]() $\Gamma , \Delta $
, we have
$\Gamma , \Delta $
, we have
![]() $\Gamma \vDash _{ \mathbf {X}}^{\mathcal {C}} \Delta $
if and only if
$\Gamma \vDash _{ \mathbf {X}}^{\mathcal {C}} \Delta $
if and only if
![]() $\Gamma \models _2 \Delta $
.
$\Gamma \models _2 \Delta $
.
Before stating the main result of this paper, we justify the choice of the properties of the schemes highlighted above. Boolean normality provides an upper bound for classicality: for every consequence relation, it ensures that the arguments it supports involving negation, conjunction, and disjunction are a subset of the classical arguments (see Lemma A.1), and it is furthermore a necessary property for this to hold with
![]() $st$
-consequence relations (see Lemma A.6). Monotonicity, for the specific case of
$st$
-consequence relations (see Lemma A.6). Monotonicity, for the specific case of
![]() $st$
, provides a lower bound: it ensures that the classical inferences are a subset of the ones supported (Lemma A.4). Collapsibility, finally, provides either a lower bound or an upper bound, depending on which consequence is considered (Lemmas A.3, A.2, A.12, and A.9).
$st$
, provides a lower bound: it ensures that the classical inferences are a subset of the ones supported (Lemma A.4). Collapsibility, finally, provides either a lower bound or an upper bound, depending on which consequence is considered (Lemmas A.3, A.2, A.12, and A.9).
3 Main characterization results
With these ingredients in place we are ready to present the main results of this paper. The results fall in two main classes: each of the consequence relations
![]() $st, ss, tt$
supports a positive characterization of classical logic;
$st, ss, tt$
supports a positive characterization of classical logic;
![]() $ss\cap tt$
and
$ss\cap tt$
and
![]() $ts$
, on the other hand, fail to support classical logic for any scheme. We start with the presentation of those negative results, for which the explanation is straightforward, reading Figure 2 bottom up.
$ts$
, on the other hand, fail to support classical logic for any scheme. We start with the presentation of those negative results, for which the explanation is straightforward, reading Figure 2 bottom up.
3.1 Negative results:
 $ts$
and
$ts$
and
 $ss \cap tt$
$ss \cap tt$
As is well-known, the consequence relation
![]() $ts$
is nonreflexive; hence, no scheme can combine with it to make it classical.
$ts$
is nonreflexive; hence, no scheme can combine with it to make it classical.
Theorem 3.1.
![]() $\vDash ^{ts}_{\mathbf {X}} \ \neq \ \vDash _{2}$
, for every three-valued scheme
$\vDash ^{ts}_{\mathbf {X}} \ \neq \ \vDash _{2}$
, for every three-valued scheme
![]() $\mathbf {X}$
.
$\mathbf {X}$
.
Proof. For an atomic proposition p, independently of
![]() $\mathbf {X}$
,
$\mathbf {X}$
,
![]() $p \vDash ^{ts}_{\mathbf {X}} p$
does not hold, whereas
$p \vDash ^{ts}_{\mathbf {X}} p$
does not hold, whereas
![]() $p \vDash _{2} p$
does.
$p \vDash _{2} p$
does.
In Section 4.1 and in Appendix B we will show that inferential classicality can be obtained inductively from two parts, essentially distinguishing the role of formulae with and without connectives: (i) a structural property for atomic propositions (namely reflexivity) and (ii) Gentzen-regularity for the connectives. Here, with
![]() $ts$
we see how the first condition is broken and prevents inferential classicality, independently of the connectives.
$ts$
we see how the first condition is broken and prevents inferential classicality, independently of the connectives.
From a structural point of view,
![]() $ss\cap tt$
is a Tarskian relation, unlike
$ss\cap tt$
is a Tarskian relation, unlike
![]() $ts$
: it is reflexive, monotonic, and transitive. Despite that, it fails to support classical logic. As the following result shows, it cannot support both the Law of Excluded Middle and the principle of Explosion in a way that makes negation coherent.
$ts$
: it is reflexive, monotonic, and transitive. Despite that, it fails to support classical logic. As the following result shows, it cannot support both the Law of Excluded Middle and the principle of Explosion in a way that makes negation coherent.
Theorem 3.2.
![]() $\vDash ^{ss\cap tt}_{\mathbf {X}} \ \neq \ \vDash _{2}$
, for every three-valued scheme
$\vDash ^{ss\cap tt}_{\mathbf {X}} \ \neq \ \vDash _{2}$
, for every three-valued scheme
![]() $\mathbf {X}$
.
$\mathbf {X}$
.
Proof. First, consider a formula p and a valuation v in which
![]() . For the classical inference
. For the classical inference
![]() $\vDash _{2} p, \neg p$
to
$\vDash _{2} p, \neg p$
to
![]() $ss \cap tt$
-hold, it must be that
$ss \cap tt$
-hold, it must be that
![]() $v(\neg p)=1$
, that is,
$v(\neg p)=1$
, that is,
![]() . Second, consider atomic formulae p, q and a valuation v in which
. Second, consider atomic formulae p, q and a valuation v in which
![]() and
and
![]() $v(q)=0$
. For the classical inference
$v(q)=0$
. For the classical inference
![]() $p, \neg p \vDash _{2} q$
to
$p, \neg p \vDash _{2} q$
to
![]() $ss \cap tt$
-hold, it must be the case that
$ss \cap tt$
-hold, it must be the case that
![]() . Contradiction.
. Contradiction.
This result is closely related to Theorem 4.3 of [Reference Chemla and Égré6], showing that
![]() $ss\cap tt$
admits no Gentzen-regular negation. The result holds even when the consequence relation is restricted to single conclusions. To validate explosion, the negation of
$ss\cap tt$
admits no Gentzen-regular negation. The result holds even when the consequence relation is restricted to single conclusions. To validate explosion, the negation of
![]() $1$
and of
$1$
and of
![]() must be
must be
![]() $0$
. To satisfy the entailment from p to
$0$
. To satisfy the entailment from p to
![]() $\neg \neg p$
the negation of
$\neg \neg p$
the negation of
![]() $0$
must be different from
$0$
must be different from
![]() $0$
when p is valued to
$0$
when p is valued to
![]() . To satisfy the converse entailment from
. To satisfy the converse entailment from
![]() $\neg \neg p$
to p, the negation of
$\neg \neg p$
to p, the negation of
![]() $0$
cannot be 1, so must be
$0$
cannot be 1, so must be
![]() . But then when p is valued to
. But then when p is valued to
![]() $1$
,
$1$
,
![]() $\neg \neg p$
is valued to
$\neg \neg p$
is valued to
![]() , so p cannot entail
, so p cannot entail
![]() $\neg \neg p$
in all cases.
$\neg \neg p$
in all cases.
A takeaway message from this result is that when entertaining the
![]() $ss \cap tt$
definition of logical consequence, there isn’t any three-valued scheme
$ss \cap tt$
definition of logical consequence, there isn’t any three-valued scheme
![]() $\mathbf {X}$
that supports the same valid inferences as the two-valued presentation of classical logic, mainly because there isn’t a truth table for negation that supports the same valid inferences in that respect. But the problem isn’t restricted to negation: as shown in [Reference Chemla and Égré6], other connectives also cannot find an appropriate truth table so as to validate the intended inferences, for example, the material conditional. Interestingly enough, however, in [Reference Chemla and Égré6] it is shown that some connectives (like conjunction and disjunction) do have compatible truth tables that validate the target inferences—at least in the restricted language where only those connectives are featured.Footnote
6
$\mathbf {X}$
that supports the same valid inferences as the two-valued presentation of classical logic, mainly because there isn’t a truth table for negation that supports the same valid inferences in that respect. But the problem isn’t restricted to negation: as shown in [Reference Chemla and Égré6], other connectives also cannot find an appropriate truth table so as to validate the intended inferences, for example, the material conditional. Interestingly enough, however, in [Reference Chemla and Égré6] it is shown that some connectives (like conjunction and disjunction) do have compatible truth tables that validate the target inferences—at least in the restricted language where only those connectives are featured.Footnote
6
Before turning to the positive results, it is important to mention that the negative results presented in this section can be easily generalized to many-valued semantics with more than three values, since the proofs of these statements appear to be independent of the number of nonclassical values. The natural requirement for this generalization is that the
![]() $ts$
-consequence relation defined for this many-valued semantics be nonreflexive and that the
$ts$
-consequence relation defined for this many-valued semantics be nonreflexive and that the
![]() $ss\cap tt$
be such that
$ss\cap tt$
be such that
![]() $ss$
lacks tautologies and
$ss$
lacks tautologies and
![]() $tt$
lacks logical contradictions.
$tt$
lacks logical contradictions.
3.2 Positive results:
 $ss$
,
$ss$
,
 $tt$
, and
$tt$
, and
 $st$
$st$
The fact that
![]() $ss$
and
$ss$
and
![]() $tt$
can support classical logic separately follows from the simple fact that the value
$tt$
can support classical logic separately follows from the simple fact that the value
![]() can be made to mirror the role of either
can be made to mirror the role of either
![]() $0$
or
$0$
or
![]() $1$
in a given scheme. This is the sense in which collapsibility (whether for falsity, or truth) yields classical logic.
$1$
in a given scheme. This is the sense in which collapsibility (whether for falsity, or truth) yields classical logic.
Theorem 3.3. Let
![]() $\mathbf {X}$
be a three-valued scheme.
$\mathbf {X}$
be a three-valued scheme.
![]() $\vDash ^{ss}_{\mathbf {X}} \ = \ \vDash _{2}$
if and only if
$\vDash ^{ss}_{\mathbf {X}} \ = \ \vDash _{2}$
if and only if
![]() $\mathbf {X}$
is falsity-collapsible
$\mathbf {X}$
is falsity-collapsible
![]() $($
see Figure 6
$($
see Figure 6
![]() $)$
.
$)$
.
Theorem 3.4. Let
![]() $\mathbf {X}$
be a three-valued scheme.
$\mathbf {X}$
be a three-valued scheme.
![]() $\vDash ^{tt}_{\mathbf {X}} \ = \ \vDash _{2}$
if and only if
$\vDash ^{tt}_{\mathbf {X}} \ = \ \vDash _{2}$
if and only if
![]() $\mathbf {X}$
is truth-collapsible
$\mathbf {X}$
is truth-collapsible
![]() $($
see Figure 5
$($
see Figure 5
![]() $)$
.
$)$
.
One direction to those two results—the one stating the sufficient conditions—is not surprising, arguably:
![]() $ss$
and
$ss$
and
![]() $tt$
are pure consequence relations, i.e., can be formulated as preservation of some set of values, usually called designated values. In this sense, the set of designated values that characterizes
$tt$
are pure consequence relations, i.e., can be formulated as preservation of some set of values, usually called designated values. In this sense, the set of designated values that characterizes
![]() $ss$
-validity consists in the singleton
$ss$
-validity consists in the singleton
![]() $\{1\}$
, while
$\{1\}$
, while
![]() $tt$
-validity can be characterized as preserving the values in the set
$tt$
-validity can be characterized as preserving the values in the set
![]() . If we think of designated values as representing truth and undesignated values as representing falsity, the results above are foreseeable. In
. If we think of designated values as representing truth and undesignated values as representing falsity, the results above are foreseeable. In
![]() $ss$
, the intermediate value doesn’t belong to the set of designated values: that is why the falsity-collapsible schema works. On the other hand, in
$ss$
, the intermediate value doesn’t belong to the set of designated values: that is why the falsity-collapsible schema works. On the other hand, in
![]() $tt$
, the intermediate value belongs to the set of designated values, and in this case, the truth-collapsible schema works. However, the other direction of these results—the one stating the necessary conditions—is more surprising in that no other schemes than those collapsible work in the intended way.
$tt$
, the intermediate value belongs to the set of designated values, and in this case, the truth-collapsible schema works. However, the other direction of these results—the one stating the necessary conditions—is more surprising in that no other schemes than those collapsible work in the intended way.
The case of
![]() $st$
is the least straightforward among the five trivalent consequence relations examined here. For this scheme we get a disjunctive characterization involving collapsibility and monotonicity as separate conditions. One way in which this may be understood is by looking at negation first: when negation is monotonic, the value
$st$
is the least straightforward among the five trivalent consequence relations examined here. For this scheme we get a disjunctive characterization involving collapsibility and monotonicity as separate conditions. One way in which this may be understood is by looking at negation first: when negation is monotonic, the value
![]() cannot be interpreted uniformly as
cannot be interpreted uniformly as
![]() $1$
or
$1$
or
![]() $0$
, and likewise for the other connectives. When negation is collapsible, then
$0$
, and likewise for the other connectives. When negation is collapsible, then
![]() can be thought of as playing the role of
can be thought of as playing the role of
![]() $1$
or
$1$
or
![]() $0$
across connectives.
$0$
across connectives.
Theorem 3.5. Let
![]() $\mathbf {X}$
be a three-valued scheme.
$\mathbf {X}$
be a three-valued scheme.
![]() $\vDash ^{st}_{\mathbf {X}} \ = \ \vDash _{2}$
if and only if
$\vDash ^{st}_{\mathbf {X}} \ = \ \vDash _{2}$
if and only if
![]() $\mathbf {X}$
is Boolean normal and either monotonic
$\mathbf {X}$
is Boolean normal and either monotonic
![]() $($
see Figure 4
$($
see Figure 4
![]() $)$
or collapsible
$)$
or collapsible
![]() $($
see Figures 7 and 8
$($
see Figures 7 and 8
![]() $)$
.
$)$
.
It follows from Theorem 3.3, using the
![]() $ss$
-consequence relation, that there are 8192 different three-valued presentations of classical logic. Similarly, according to Theorem 3.4, we can obtain also 8192 different three-valued presentations of classical logic using the
$ss$
-consequence relation, that there are 8192 different three-valued presentations of classical logic. Similarly, according to Theorem 3.4, we can obtain also 8192 different three-valued presentations of classical logic using the
![]() $tt$
-consequence relation. Finally, as a consequence of Theorem 3.5 there are 528 different three-valued presentations of classical logic, with the
$tt$
-consequence relation. Finally, as a consequence of Theorem 3.5 there are 528 different three-valued presentations of classical logic, with the
![]() $st$
-consequence relation.
$st$
-consequence relation.
In the next section, we explore how all of these results can be connected with similar investigations about whether
![]() $ss$
,
$ss$
,
![]() $tt$
,
$tt$
,
![]() $st$
and
$st$
and
![]() $ts$
and
$ts$
and
![]() $ss\cap tt$
can support the operational rules of Gentzen’s proof system for classical logic.
$ss\cap tt$
can support the operational rules of Gentzen’s proof system for classical logic.
4 Comparisons and perspectives
The results of the previous sections tell us, given a three-valued definition of validity, exactly which three-valued truth tables for negation, conjunction, and disjunction warrant classical inferences for the resulting logic. In Section 4.1, we compare this finding to results established in [Reference Chemla and Égré6]. In Section 4.2 we discuss some philosophical implications of our work regarding the definition of classical logic.
4.1 Gentzen-regular connectives
In [Reference Chemla and Égré6], a goal partly related to the one discussed here was pursued. Namely, given a three-valued definition of validity, it was asked which three-valued operators are Gentzen-regular relative to it. Basically, a Gentzen-regular connective is a connective whose behavior can be characterized in terms of the bidirectional rules of Gentzen’s
![]() $\mathbf {LK}$
—these rules can therefore be understood as introduction and elimination sequent rules, respectively. For example, the rule whereby
$\mathbf {LK}$
—these rules can therefore be understood as introduction and elimination sequent rules, respectively. For example, the rule whereby
![]() $\Gamma , A, B\vdash \Delta $
iff
$\Gamma , A, B\vdash \Delta $
iff
![]() $\Gamma , A\wedge B\vdash \Delta $
corresponds to Gentzen’s rule when conjunction occurs in premise position. And the rule whereby
$\Gamma , A\wedge B\vdash \Delta $
corresponds to Gentzen’s rule when conjunction occurs in premise position. And the rule whereby
![]() $\Gamma \vdash A\wedge B, \Delta $
iff
$\Gamma \vdash A\wedge B, \Delta $
iff
![]() $\Gamma \vdash A, \Delta $
and
$\Gamma \vdash A, \Delta $
and
![]() $\Gamma \vdash B, \Delta $
corresponds to Gentzen’s rule for conjunction in conclusion position (see also Figure 1). We give a more precise definition of Gentzen-regularity in Appendix B, since the definition applies to any n-ary connective, beyond negation, conjunction, and disjunction.
$\Gamma \vdash B, \Delta $
corresponds to Gentzen’s rule for conjunction in conclusion position (see also Figure 1). We give a more precise definition of Gentzen-regularity in Appendix B, since the definition applies to any n-ary connective, beyond negation, conjunction, and disjunction.
Clearly, when dealing with the usual two-valued semantics for classical logic, all connectives are Gentzen-regular. However, a consequence relation can fail to be classical at the structural level, but still admit Gentzen-regular connectives. This means that unlike us here, [Reference Chemla and Égré6] did not seek a three-valued characterization of classical logic qua combination of operational and structural rules. Instead they focused merely on the operational side of Gentzen’s proof system for classical logic.
Furthermore, [Reference Chemla and Égré6]’s results did not seek to characterize schemes (namely sets of truth tables), but they look at connectives one by one. Consequently, their approach is not limited to negation, conjunction and disjunction, or to a particular set of operators, but it covers arbitrary n-ary truth-functional operators. However, they assume the language to be constant-expressive, which means that the constants
![]() $1$
,
$1$
,
![]() $0$
and
$0$
and
![]() are expressible by means of constant symbols.
are expressible by means of constant symbols.
For comparison, let us consider
![]() $st$
and
$st$
and
![]() $ts$
first. Under the assumption of constant expressiveness, [Reference Chemla and Égré6] proved that
$ts$
first. Under the assumption of constant expressiveness, [Reference Chemla and Égré6] proved that
![]() $st$
and
$st$
and
![]() $ts$
admit a unique Gentzen-regular negation, a unique Gentzen-regular conjunction, and a unique Gentzen-regular disjunction, described by the Strong Kleene tables. In the case of
$ts$
admit a unique Gentzen-regular negation, a unique Gentzen-regular conjunction, and a unique Gentzen-regular disjunction, described by the Strong Kleene tables. In the case of
![]() $ts$
, it therefore admits exactly one Gentzen-regular scheme involving negation, disjunction and conjunction. Above we saw that
$ts$
, it therefore admits exactly one Gentzen-regular scheme involving negation, disjunction and conjunction. Above we saw that
![]() $ts$
admits no trivalent scheme supporting classical logic. There is no contradiction there, since Gentzen-regularity pertains only to the operational rules of a proof system for classical logic, and not to structural rules. This situation may be interpreted by saying that although
$ts$
admits no trivalent scheme supporting classical logic. There is no contradiction there, since Gentzen-regularity pertains only to the operational rules of a proof system for classical logic, and not to structural rules. This situation may be interpreted by saying that although
![]() $ts$
does not support classical inferences, it can support Gentzen-regular connectives that describe, in a way, classical connectives.
$ts$
does not support classical inferences, it can support Gentzen-regular connectives that describe, in a way, classical connectives.
For
![]() $st$
, the situation is different: as mentioned in the previous section, Figures 4, 7 and 8 together indicate that
$st$
, the situation is different: as mentioned in the previous section, Figures 4, 7 and 8 together indicate that
![]() $st$
admits 528 distinct schemes involving negation, conjunction and disjunction, supporting classical inferences, including the Weak Kleene scheme and more (512 collapsible schemes and 16 monotone schemes). However, [Reference Chemla and Égré6]’s result implies that
$st$
admits 528 distinct schemes involving negation, conjunction and disjunction, supporting classical inferences, including the Weak Kleene scheme and more (512 collapsible schemes and 16 monotone schemes). However, [Reference Chemla and Égré6]’s result implies that
![]() $st$
admits a unique Gentzen-regular scheme, namely the Strong Kleene one. Whence comes the difference? Here the answer concerns the assumption of constant expressiveness. In [Reference Chemla and Égré6], Chemla and Egré left as an open issue the characterization of Gentzen-regular three-valued operators when the language does not admit constants for all truth-values. The present inventory can be seen as answering this problem for the case in which the constants are not expressible.
$st$
admits a unique Gentzen-regular scheme, namely the Strong Kleene one. Whence comes the difference? Here the answer concerns the assumption of constant expressiveness. In [Reference Chemla and Égré6], Chemla and Egré left as an open issue the characterization of Gentzen-regular three-valued operators when the language does not admit constants for all truth-values. The present inventory can be seen as answering this problem for the case in which the constants are not expressible.
These comparisons raise the more general question of what may be needed beside the Gentzen-regularity of a connective in order to guarantee that the logic be inferentially classical. The following result gives an answer to this question:
Lemma 4.1. A propositional logic
![]() $L=\langle \vdash , C\rangle $
is
$L=\langle \vdash , C\rangle $
is
![]() $($
inferentially
$($
inferentially
![]() $)$
classical if and only if its connectives in C are Gentzen-regular and
$)$
classical if and only if its connectives in C are Gentzen-regular and
![]() $\vdash $
is such that for
$\vdash $
is such that for
![]() $\Gamma $
and
$\Gamma $
and
![]() $\Delta $
two sets of atomic propositions,
$\Delta $
two sets of atomic propositions,
![]() $\Gamma \vdash \Delta $
iff
$\Gamma \vdash \Delta $
iff
![]() $\Gamma \cap \Delta \neq \emptyset $
.
$\Gamma \cap \Delta \neq \emptyset $
.
Proof. See Appendix B.
A consequence relation like
![]() $ts$
obviously fails the structural condition expressed in this lemma, and so cannot support classical logic despite admitting Gentzen-regular connectives. On the other hand,
$ts$
obviously fails the structural condition expressed in this lemma, and so cannot support classical logic despite admitting Gentzen-regular connectives. On the other hand,
![]() $st$
satisfies the condition, just like
$st$
satisfies the condition, just like
![]() $ss$
and
$ss$
and
![]() $tt$
. Finally, while
$tt$
. Finally, while
![]() $ss\cap tt$
too satisfies it, it is shown in [Reference Chemla and Égré6] that it does not admit a Gentzen-regular negation.
$ss\cap tt$
too satisfies it, it is shown in [Reference Chemla and Égré6] that it does not admit a Gentzen-regular negation.
More generally, we believe the above lemma could be used to answer the question we posed relative to arbitrary connectives beside negation, conjunction and disjunction, drawing on the fact that the notion of Gentzen-regularity can be defined for arbitrary finite operators as discussed in [Reference Chemla and Égré6]. We leave this investigation for future work.
4.2 Philosophical perspectives
The results of this paper show that classical logic can be obtained in a variety of ways in a three-valued setting. This raises the following question: from these various presentations of classical logic, is one of them more fundamental than the others? Besides, aren’t all of them just superfluous in comparison to the standard two-valued presentation of classical logic?
Let us consider
![]() $ss$
and
$ss$
and
![]() $tt$
first. Relative to those systems, Theorems 3.3 and 3.4 establish that the collapsible schemes support exactly the classical inferences. But they are also schemes in which the middle value mirrors exactly one of the classical values. Hence, this middle value may be judged entirely redundant. We can find instances of this observation in the literature. In [Reference Cantwell3], for instance, Cantwell puts forward a system of trivalent truth tables for negation, conjunction, disjunction, and a conditional operator. This system turns out to encapsulate exactly one of the truth-collapsible schemes of Figure 5, and it is called “Non-Bivalent Classical” by Cantwell, precisely because it yields classical logic when paired with
$tt$
first. Relative to those systems, Theorems 3.3 and 3.4 establish that the collapsible schemes support exactly the classical inferences. But they are also schemes in which the middle value mirrors exactly one of the classical values. Hence, this middle value may be judged entirely redundant. We can find instances of this observation in the literature. In [Reference Cantwell3], for instance, Cantwell puts forward a system of trivalent truth tables for negation, conjunction, disjunction, and a conditional operator. This system turns out to encapsulate exactly one of the truth-collapsible schemes of Figure 5, and it is called “Non-Bivalent Classical” by Cantwell, precisely because it yields classical logic when paired with
![]() $tt$
-validity, as presented in [Reference Cantwell3, Theorem 4.4]. In this regard, the interest of Cantwell’s conditional operator—proposed earlier by [Reference Cooper10] (see [Reference Égré, Rossi and Sprenger13] for a comparison)—shows up precisely when his conjunction, disjunction and conditional are paired with the Strong Kleene negation so as to yield a noncollapsible, nonclassical system.
$tt$
-validity, as presented in [Reference Cantwell3, Theorem 4.4]. In this regard, the interest of Cantwell’s conditional operator—proposed earlier by [Reference Cooper10] (see [Reference Égré, Rossi and Sprenger13] for a comparison)—shows up precisely when his conjunction, disjunction and conditional are paired with the Strong Kleene negation so as to yield a noncollapsible, nonclassical system.
More generally, the collapsible schemes can be applied a reduction technique on truth values presented as a “grouping reduction” in [Reference Chemla and Égré5, Appendix C], whose goal is precisely to merge truth values that play the same role in premise position and in conclusion positions of arguments. As shown there, for
![]() $ss$
and
$ss$
and
![]() $tt$
, grouping reductions basically fulfill Suszko’s goal in [Reference Suszko31]: they suggest that an appeal to three truth values is idle when it comes to representing classical inferences in a compositional way, and that two values are all we need.
$tt$
, grouping reductions basically fulfill Suszko’s goal in [Reference Suszko31]: they suggest that an appeal to three truth values is idle when it comes to representing classical inferences in a compositional way, and that two values are all we need.
What about
![]() $st$
? It was proved that the determination of the minimum number of truth values needed to represent a reflexive, monotonic and transitive consequence relation is exactly two, but that it is three if the relation is reflexive and monotonic but nontransitive (viz. [Reference Chemla and Égré5, Corollary 4.7]). But as shown by [Reference Barrio, Rosenblatt and Tajer1, Reference Cobreros, Égré, Ripley and van Rooij8, Reference Dicher, Paoli, Başkent and Ferguson11],
$st$
? It was proved that the determination of the minimum number of truth values needed to represent a reflexive, monotonic and transitive consequence relation is exactly two, but that it is three if the relation is reflexive and monotonic but nontransitive (viz. [Reference Chemla and Égré5, Corollary 4.7]). But as shown by [Reference Barrio, Rosenblatt and Tajer1, Reference Cobreros, Égré, Ripley and van Rooij8, Reference Dicher, Paoli, Başkent and Ferguson11],
![]() $st$
is not a transitive consequence relation. For
$st$
is not a transitive consequence relation. For
![]() $st$
, therefore, we cannot argue in the same way as for
$st$
, therefore, we cannot argue in the same way as for
![]() $ss$
- and
$ss$
- and
![]() $tt$
-systems that three values are idle in comparison to using just two values. Besides, as argued by [Reference Cobreros, Égré, Ripley and van Rooij8, Reference Szmuc and Ferguson32], the use of a third truth value is independently motivated to represent special semantic status, such as vagueness, or absurdity, or paradoxicality. And for systems of inferences involving sentences with this third semantic status, preserving classical logic for inferences is a conservative benefit.Footnote
7
$tt$
-systems that three values are idle in comparison to using just two values. Besides, as argued by [Reference Cobreros, Égré, Ripley and van Rooij8, Reference Szmuc and Ferguson32], the use of a third truth value is independently motivated to represent special semantic status, such as vagueness, or absurdity, or paradoxicality. And for systems of inferences involving sentences with this third semantic status, preserving classical logic for inferences is a conservative benefit.Footnote
7
We can therefore answer the questions raised above as follows: for consequence relations like
![]() $ss$
and
$ss$
and
![]() $tt$
, collapsible schemes constitute roundabout ways of representing classical logic compared to the two-valued definition. In the case of
$tt$
, collapsible schemes constitute roundabout ways of representing classical logic compared to the two-valued definition. In the case of
![]() $st$
, the situation is more complex: while the two-valued approach to classical logic sets a benchmark for the definition of classicality all across the board, we may find different foundations for classicality at the inferential level. At this point, however, some work remains to be done to generalize the present results to more connectives, but also to many-valued logics beyond three values.Footnote
8
Furthermore, the present investigations are limited to the propositional case, but one may also be interested in looking at the question of which are all the three-valued presentations of classical logic when such a system is understood as first-order logic. Interestingly enough, the generalizations of the previously discussed results are not always immediate, and the issue is somehow related to the understanding of the universal and existential quantifiers as infinitary versions of conjunction and disjunction, respectively.Footnote
9
$st$
, the situation is more complex: while the two-valued approach to classical logic sets a benchmark for the definition of classicality all across the board, we may find different foundations for classicality at the inferential level. At this point, however, some work remains to be done to generalize the present results to more connectives, but also to many-valued logics beyond three values.Footnote
8
Furthermore, the present investigations are limited to the propositional case, but one may also be interested in looking at the question of which are all the three-valued presentations of classical logic when such a system is understood as first-order logic. Interestingly enough, the generalizations of the previously discussed results are not always immediate, and the issue is somehow related to the understanding of the universal and existential quantifiers as infinitary versions of conjunction and disjunction, respectively.Footnote
9
A Appendix: proofs
A.1 Proofs common to several consequence relations
Lemma A.1. Let
![]() $\mathbf {X}$
be a three-valued scheme. If
$\mathbf {X}$
be a three-valued scheme. If
![]() $\mathbf {X}$
is Boolean normal, then
$\mathbf {X}$
is Boolean normal, then
![]() $\vDash ^{\mathcal {C}}_{\mathbf {X}} \ \subseteq \ \vDash _{2}$
, with
$\vDash ^{\mathcal {C}}_{\mathbf {X}} \ \subseteq \ \vDash _{2}$
, with
![]() $\mathcal {C}\in \{ss,tt,st\}$
.
$\mathcal {C}\in \{ss,tt,st\}$
.
Proof. We need to prove that if
![]() $\Gamma \nvDash _{2} \Delta $
then
$\Gamma \nvDash _{2} \Delta $
then
![]() $\Gamma \nvDash ^{\mathcal {C}}_{\mathbf {X}} \Delta $
, for every
$\Gamma \nvDash ^{\mathcal {C}}_{\mathbf {X}} \Delta $
, for every
![]() $\Gamma , \Delta $
. By a straightforward induction, under the assumption of Boolean normality, it is easy to show that for every classical two-valued valuation
$\Gamma , \Delta $
. By a straightforward induction, under the assumption of Boolean normality, it is easy to show that for every classical two-valued valuation
![]() $v$
, there is a three-valued
$v$
, there is a three-valued
![]() $\mathbf {X}$
valuation
$\mathbf {X}$
valuation
![]() $v^{*}$
such that
$v^{*}$
such that
![]() $v=v^{*}$
. Thus given the notions of
$v=v^{*}$
. Thus given the notions of
![]() $ss$
-,
$ss$
-,
![]() $tt$
- and
$tt$
- and
![]() $st$
-consequence relations, if v is a witness of
$st$
-consequence relations, if v is a witness of
![]() $\Gamma \nvDash _{2} \Delta $
, then
$\Gamma \nvDash _{2} \Delta $
, then
![]() $v^{*}$
is a witness of
$v^{*}$
is a witness of
![]() $\Gamma \nvDash ^{\mathcal {C}}_{\mathbf {X}} \Delta $
.
$\Gamma \nvDash ^{\mathcal {C}}_{\mathbf {X}} \Delta $
.
Lemma A.2. Let
![]() $\mathbf {X}$
be a three-valued scheme. If
$\mathbf {X}$
be a three-valued scheme. If
![]() $\mathbf {X}$
is falsity-collapsible, then
$\mathbf {X}$
is falsity-collapsible, then
![]() $ \vDash _{2} \ \subseteq \ \vDash ^{sy}_{\mathbf {X}}$
, with
$ \vDash _{2} \ \subseteq \ \vDash ^{sy}_{\mathbf {X}}$
, with
![]() $y \in \{s,t\}$
.
$y \in \{s,t\}$
.
Proof. Suppose
![]() $\Gamma \nvDash ^{sy}_{\mathbf {X}} \Delta $
, i.e., either there is a three-valued valuation
$\Gamma \nvDash ^{sy}_{\mathbf {X}} \Delta $
, i.e., either there is a three-valued valuation
![]() $v$
such that
$v$
such that
![]() $v(A)=1$
and
$v(A)=1$
and
![]() $v(B)=0$
, for every
$v(B)=0$
, for every
![]() $A \in \Gamma $
and
$A \in \Gamma $
and
![]() $B \in \Delta $
, if
$B \in \Delta $
, if
![]() $y=t$
, or there is a three-valued valuation
$y=t$
, or there is a three-valued valuation
![]() $v$
such that
$v$
such that
![]() $v(A)=1$
and
$v(A)=1$
and
![]() , for every
, for every
![]() $A \in \Gamma $
and
$A \in \Gamma $
and
![]() $B \in \Delta $
, if
$B \in \Delta $
, if
![]() $y=s$
.
$y=s$
.
Now we will show that in both cases
![]() $\Gamma \nvDash _{2} \Delta $
, i.e., that there is a classical two-valued valuation
$\Gamma \nvDash _{2} \Delta $
, i.e., that there is a classical two-valued valuation
![]() $v^{*}$
such that
$v^{*}$
such that
![]() $v^{*}(A)=1$
and
$v^{*}(A)=1$
and
![]() $v^{*}(B)=0$
, for every
$v^{*}(B)=0$
, for every
![]() $A \in \Gamma $
and
$A \in \Gamma $
and
![]() $B \in \Delta $
. Consider any of the cases and take
$B \in \Delta $
. Consider any of the cases and take
![]() $v^{*}$
to be defined as follows:
$v^{*}$
to be defined as follows:

Now we show by induction on the complexity of the formula that, on the one hand, if
![]() $v(A)=1$
, then
$v(A)=1$
, then
![]() $v^{*}(A)=1$
and, on the other hand, if
$v^{*}(A)=1$
and, on the other hand, if
![]() , then
, then
![]() $v^{*}(A)=0$
.
$v^{*}(A)=0$
.
Base case: If A is a propositional letter, then it holds by definition of the valuation
![]() $v^{*}$
.
$v^{*}$
.
Inductive step: Here we need to consider three cases:
-
•
 $A = \neg B$
.
$A = \neg B$
.-
– If
 $v(\neg B)= 1$
then
$v(\neg B)= 1$
then
 . By IH
. By IH
 $v^{*}(B)=0$
, then
$v^{*}(B)=0$
, then
 $v^{*}(\neg B)=1$
.
$v^{*}(\neg B)=1$
. -
– If
 then
then
 $v(B)= 1$
. By IH
$v(B)= 1$
. By IH
 $v^{*}(B)=1$
, then
$v^{*}(B)=1$
, then
 $v^{*}(\neg B)=0$
.
$v^{*}(\neg B)=0$
.
-
-
•
 $A = B \wedge C$
.
$A = B \wedge C$
.-
– If
 $v(B \wedge C)= 1$
then
$v(B \wedge C)= 1$
then
 $v(B)=v(C)=1$
. By IH
$v(B)=v(C)=1$
. By IH
 $v^{*}(B)=v^{*}(C)=1$
, then
$v^{*}(B)=v^{*}(C)=1$
, then
 $v^{*}(B \wedge C)=1$
.
$v^{*}(B \wedge C)=1$
. -
– If
 then
then
 and
and
 . By IH
. By IH
 $v^{*}(B)=v^{*}(C)=0$
, and then
$v^{*}(B)=v^{*}(C)=0$
, and then
 $v^{*}(B \wedge C)=0$
.
$v^{*}(B \wedge C)=0$
.
-
-
•
 $A = B \vee C$
.
$A = B \vee C$
.-
– If
 $v(B \vee C)= 1$
then
$v(B \vee C)= 1$
then
 $v(B)=1$
or
$v(B)=1$
or
 $v(C)=1$
. So, depending on which of these two is the case, by IH
$v(C)=1$
. So, depending on which of these two is the case, by IH
 $v^{*}(B)=1$
or
$v^{*}(B)=1$
or
 $v^{*}(C)=1$
, and then
$v^{*}(C)=1$
, and then
 $v^{*}(B \vee C)=1$
.
$v^{*}(B \vee C)=1$
. -
– If
 then
then
 and
and
 . By IH
. By IH
 $v^{*}(B)=v^{*}(C)=0$
, then
$v^{*}(B)=v^{*}(C)=0$
, then
 $v^{*}(B \vee C)=0$
.
$v^{*}(B \vee C)=0$
.
-
This shows
![]() $v^{*}$
is a classical two-valued valuation witnessing
$v^{*}$
is a classical two-valued valuation witnessing
![]() $\Gamma \nvDash _{2} \Delta $
, and therefore that
$\Gamma \nvDash _{2} \Delta $
, and therefore that
![]() $\vDash _{2} \ \subseteq \ \vDash ^{st}_{\mathbf {X}}$
as desired.
$\vDash _{2} \ \subseteq \ \vDash ^{st}_{\mathbf {X}}$
as desired.
Lemma A.3. Let
![]() $\mathbf {X}$
be a three-valued scheme. If
$\mathbf {X}$
be a three-valued scheme. If
![]() $\mathbf {X}$
is truth-collapsible, then
$\mathbf {X}$
is truth-collapsible, then
![]() $ \vDash _{2} \ \subseteq \ \vDash ^{yt}_{\mathbf {X}}$
, with
$ \vDash _{2} \ \subseteq \ \vDash ^{yt}_{\mathbf {X}}$
, with
![]() $y \in \{s,t\}$
.
$y \in \{s,t\}$
.
Proof. The proof is similar to the previous lemma, and so we leave it to the reader.
A.2 The proofs for
 $st$
$st$
Lemma A.4. Let
![]() $\mathbf {X}$
be a three-valued scheme. If
$\mathbf {X}$
be a three-valued scheme. If
![]() $\mathbf {X}$
is monotonic, then
$\mathbf {X}$
is monotonic, then
![]() $ \vDash _{2} \ \subseteq \ \vDash ^{st}_{\mathbf {X}}$
.
$ \vDash _{2} \ \subseteq \ \vDash ^{st}_{\mathbf {X}}$
.
Proof. Assume there is an inference such that
![]() $\Gamma \nvDash ^{st}_{\mathbf {X}}\Delta $
. Then, there is a valuation
$\Gamma \nvDash ^{st}_{\mathbf {X}}\Delta $
. Then, there is a valuation
![]() $v$
, such that
$v$
, such that
![]() $v(A)=1$
for every
$v(A)=1$
for every
![]() $A \in \Gamma $
and
$A \in \Gamma $
and
![]() $v(B)=0$
for every
$v(B)=0$
for every
![]() $B \in \Delta $
. Now we will show that
$B \in \Delta $
. Now we will show that
![]() $\Gamma \nvDash _{2} \Delta $
, i.e., that there is a classical two-valued valuation
$\Gamma \nvDash _{2} \Delta $
, i.e., that there is a classical two-valued valuation
![]() $v^{*}$
such that
$v^{*}$
such that
![]() $v^{*}(A)=1$
and
$v^{*}(A)=1$
and
![]() $v^{*}(B)=0$
, for every
$v^{*}(B)=0$
, for every
![]() $A \in \Gamma $
and
$A \in \Gamma $
and
![]() $B \in \Delta $
. We take
$B \in \Delta $
. We take
![]() $v^{*}$
to be defined as follows:
$v^{*}$
to be defined as follows:

Now we show by induction on the complexity of the formula that, on the one hand, if
![]() $v(A)=1$
, then
$v(A)=1$
, then
![]() $v^{*}(A)=1$
and, on the other hand, if
$v^{*}(A)=1$
and, on the other hand, if
![]() $v(A)=0$
, then
$v(A)=0$
, then
![]() $v^{*}(A)=0$
.
$v^{*}(A)=0$
.
Base case: If A is a propositional letter, then it holds by definition of the valuation
![]() $v^{*}$
.
$v^{*}$
.
Inductive step: Here we need to consider three cases:
-
•
 $A = \neg B$
.
$A = \neg B$
.-
– If
 $v(\neg B)= 1$
then
$v(\neg B)= 1$
then
 $v(B)=0$
. By IH
$v(B)=0$
. By IH
 $v^{*}(B)=0$
, then
$v^{*}(B)=0$
, then
 $v^{*}(\neg B)=1$
.
$v^{*}(\neg B)=1$
. -
– If
 $v(\neg B)= 0$
then
$v(\neg B)= 0$
then
 $v(B)= 1$
. By IH
$v(B)= 1$
. By IH
 $v^{*}(B)=1$
, then
$v^{*}(B)=1$
, then
 $v^{*}(\neg B)=0$
.
$v^{*}(\neg B)=0$
.
-
-
•
 $A = B \wedge C$
.
$A = B \wedge C$
.-
– If
 $v(B \wedge C)= 1$
then
$v(B \wedge C)= 1$
then
 $v(B)=v(C)=1$
. By IH
$v(B)=v(C)=1$
. By IH
 $v^{*}(B)=v^{*}(C)=1$
, then
$v^{*}(B)=v^{*}(C)=1$
, then
 $v^{*}(B \wedge C)=1$
.
$v^{*}(B \wedge C)=1$
. -
– If
 $v(B \wedge C)= 0$
then
$v(B \wedge C)= 0$
then
 $v(B)=0$
or
$v(B)=0$
or
 $v(C)=0$
. Then depending on which of the disjuncts holds, by IH
$v(C)=0$
. Then depending on which of the disjuncts holds, by IH
 $v^{*}(B)=0$
or
$v^{*}(B)=0$
or
 $v^{*}(C)=0$
, and then
$v^{*}(C)=0$
, and then
 $v^{*}(B \wedge C)=0$
.
$v^{*}(B \wedge C)=0$
.
-
-
•
 $A = B \vee C$
.
$A = B \vee C$
.-
– If
 $v(B \vee C)= 1$
then
$v(B \vee C)= 1$
then
 $v(B)=1$
or
$v(B)=1$
or
 $v(C)=1$
. So, depending on which of these two is the case, by IH
$v(C)=1$
. So, depending on which of these two is the case, by IH
 $v^{*}(B)=1$
or
$v^{*}(B)=1$
or
 $v^{*}(C)=1$
, and then
$v^{*}(C)=1$
, and then
 $v^{*}(B \vee C)=1$
.
$v^{*}(B \vee C)=1$
. -
– If
 $v(B \vee C)= 0$
then
$v(B \vee C)= 0$
then
 $v(B) =0$
and
$v(B) =0$
and
 $v(C)=0$
. By IH
$v(C)=0$
. By IH
 $v^{*}(B)=v^{*}(C)=0$
, then
$v^{*}(B)=v^{*}(C)=0$
, then
 $v^{*}(B \vee C)=0$
.
$v^{*}(B \vee C)=0$
.
-
This shows
![]() $v^{*}$
is a classical two-valued valuation witnessing
$v^{*}$
is a classical two-valued valuation witnessing
![]() $\Gamma \nvDash _{2}\Delta $
, and therefore that
$\Gamma \nvDash _{2}\Delta $
, and therefore that
![]() $\vDash _{2} \ \subseteq \ \vDash ^{st}_{\mathbf {X}}$
as desired.
$\vDash _{2} \ \subseteq \ \vDash ^{st}_{\mathbf {X}}$
as desired.
Theorem A.5. Let
![]() $\mathbf {X}$
be a three-valued scheme. If
$\mathbf {X}$
be a three-valued scheme. If
![]() $\mathbf {X}$
is Boolean normal monotonic, or Boolean normal collapsible, then
$\mathbf {X}$
is Boolean normal monotonic, or Boolean normal collapsible, then
![]() $\vDash ^{st}_{\mathbf {X}} \ = \ \vDash _{2}$
.
$\vDash ^{st}_{\mathbf {X}} \ = \ \vDash _{2}$
.
Up until now we proved that certain three-valued schemes—belonging in particular to the class of normal Boolean monotonic, or normal Boolean collapsible schemes—render classical logic when equipped with the
![]() $st$
definition of logical consequence. We proceed to prove the converse. That is to say, that if a three-valued scheme renders classical logic when equipped with the
$st$
definition of logical consequence. We proceed to prove the converse. That is to say, that if a three-valued scheme renders classical logic when equipped with the
![]() $st$
definition of logical consequence, then it belongs in one and only one of the two classes described before. However, to prove this we need some definitions and some important lemmata, that will do all the heavy-lifting for us.
$st$
definition of logical consequence, then it belongs in one and only one of the two classes described before. However, to prove this we need some definitions and some important lemmata, that will do all the heavy-lifting for us.
Lemma A.6. Let
![]() $\mathbf {X}$
be a three-valued scheme. If
$\mathbf {X}$
be a three-valued scheme. If
![]() $\mathbf {X}$
is not Boolean normal, then
$\mathbf {X}$
is not Boolean normal, then
![]() $\vDash ^{st}_{\mathbf {X}} \ \nsubseteq \ \vDash _{2}$
.
$\vDash ^{st}_{\mathbf {X}} \ \nsubseteq \ \vDash _{2}$
.
Proof. Suppose
![]() $\mathbf {X}$
is not Boolean normal, then some operation behaves in a way such that some classically invalid inferences are valid in
$\mathbf {X}$
is not Boolean normal, then some operation behaves in a way such that some classically invalid inferences are valid in
![]() $\mathbf {X}$
.
$\mathbf {X}$
.
-
1. Let’s start with negation. If
 $\mathbf {X}$
is such that
$\mathbf {X}$
is such that
 then
then
 $ p \vDash ^{st}_{\mathbf {X}}\neg p$
. On the other hand if
$ p \vDash ^{st}_{\mathbf {X}}\neg p$
. On the other hand if
 , then
, then
 $ \neg p \vDash ^{st}_{\mathbf {X}} p$
.
$ \neg p \vDash ^{st}_{\mathbf {X}} p$
. -
2. So, having proved that negation must be Boolean normal, if it is
 $\vee $
which is not Boolean normal, then
$\vee $
which is not Boolean normal, then
 $ \neg p \vee \neg p \vDash ^{st}_{\mathbf {X}} p$
, or
$ \neg p \vee \neg p \vDash ^{st}_{\mathbf {X}} p$
, or
 $\neg p \vee p \vDash ^{st}_{\mathbf {X}} p$
, or
$\neg p \vee p \vDash ^{st}_{\mathbf {X}} p$
, or
 $ p \vDash ^{st}_{\mathbf {X}} \neg p \vee \neg p$
$ p \vDash ^{st}_{\mathbf {X}} \neg p \vee \neg p$
-
3. Again, knowing that negation is Boolean normal, if it is
 $\wedge $
which is not Boolean normal, then
$\wedge $
which is not Boolean normal, then
 $ p \vDash ^{st}_{\mathbf {X}} p \wedge \neg p$
, or
$ p \vDash ^{st}_{\mathbf {X}} p \wedge \neg p$
, or
 $ \neg p \wedge \neg p \vDash ^{st}_{\mathbf {X}} p$
, or
$ \neg p \wedge \neg p \vDash ^{st}_{\mathbf {X}} p$
, or
 $p \vDash ^{st}_{\mathbf {X}} \neg p \wedge \neg p$
$p \vDash ^{st}_{\mathbf {X}} \neg p \wedge \neg p$
But none of these are valid in classical logic, whence
![]() $\vDash ^{st}_{\mathbf {X}} \ \nsubseteq \ \vDash _{2}$
.
$\vDash ^{st}_{\mathbf {X}} \ \nsubseteq \ \vDash _{2}$
.
From this lemma, since the classical values are determined, we can conclude that there are in principle at most three possible negations to consider:
![]() . What we prove next is that each of these negations selects exactly the truth tables needed to obtain classical logic.
. What we prove next is that each of these negations selects exactly the truth tables needed to obtain classical logic.
Lemma A.7. Let
![]() $\mathbf {X}$
be a three-valued scheme. If
$\mathbf {X}$
be a three-valued scheme. If
![]() $\vDash ^{st}_{\mathbf {X}} \ = \ \vDash _{2}$
we have three cases
$\vDash ^{st}_{\mathbf {X}} \ = \ \vDash _{2}$
we have three cases
![]() $:$
$:$
-
(1) If
 then conjunction and disjunction are Boolean normal monotonic
then conjunction and disjunction are Boolean normal monotonic
 $($
the operations in Figure 4
$($
the operations in Figure 4
 $)$
.
$)$
. -
(2) If
 then conjunction and disjunction are operations of a Boolean normal truth-collapsible scheme (the operations in Figure 7).
then conjunction and disjunction are operations of a Boolean normal truth-collapsible scheme (the operations in Figure 7). -
(3) If
 then conjunction and disjunction are operations of a Boolean normal falsity-collapsible scheme (the operations in Figure 8).
then conjunction and disjunction are operations of a Boolean normal falsity-collapsible scheme (the operations in Figure 8).
Proof. By Lemma A.6 we assume Boolean normality. We will prove cases (1) and (2), since (3) is similar.
-
Case (1) Assume then that
 . We will show that the other operations are monotonic.
. We will show that the other operations are monotonic.-
• The case of conjunction:
-
– First we show that in every
 $\textbf {X}$
,
$\textbf {X}$
,
 .
.-
* Assume on the contrary that
 . Then we would have a counterexample to the following classically valid inference:
. Then we would have a counterexample to the following classically valid inference:
 $ p \wedge \neg p\nvDash ^{st}_{\mathbf {X}} q$
(
$ p \wedge \neg p\nvDash ^{st}_{\mathbf {X}} q$
(
 $v(q)=0$
,
$v(q)=0$
,
 ).
). -
* Assume now that
 . Then we would have a counterexample to the following classically valid inference:
. Then we would have a counterexample to the following classically valid inference:
 $\neg (\neg p \wedge \neg p) \nvDash ^{st}_{\mathbf {X}} p \wedge p$
(
$\neg (\neg p \wedge \neg p) \nvDash ^{st}_{\mathbf {X}} p \wedge p$
(
 ).
).
-
-
– Now, having proved the previous case, we show that
 (we leave to the reader the case
(we leave to the reader the case
 ).
).-
* Assume on the contrary that
 . Then we would have a counterexample to the following classically valid inference:
. Then we would have a counterexample to the following classically valid inference:
 $ p \nvDash ^{st}_{\mathbf {X}} \neg (q \wedge \neg q)\wedge p $
(
$ p \nvDash ^{st}_{\mathbf {X}} \neg (q \wedge \neg q)\wedge p $
(
 $v(p)=1$
,
$v(p)=1$
,
 ).
). -
* Assume now that
 . Then we would have a counterexample to the following classically valid inference:
. Then we would have a counterexample to the following classically valid inference:
 $ (p \wedge \neg p) \wedge q \nvDash ^{st}_{\mathbf {X}} \neg q$
(
$ (p \wedge \neg p) \wedge q \nvDash ^{st}_{\mathbf {X}} \neg q$
(
 ,
,
 $v(q)=1$
).
$v(q)=1$
).
-
-
– We show now that
 (we leave to the reader the case
(we leave to the reader the case
 ). If it were the case that
). If it were the case that
 then we would have a counterexample to the following classically valid inference:
then we would have a counterexample to the following classically valid inference:
 $ p \wedge q \nvDash ^{st}_{\mathbf {X}} q$
(
$ p \wedge q \nvDash ^{st}_{\mathbf {X}} q$
(
 ,
,
 $v(q)=0$
).
$v(q)=0$
).
-
-
• The case of disjunction:
-
– First we show that in every
 $\textbf {X}$
,
$\textbf {X}$
,
 .
.-
* Assume on the contrary that
 . Then we would have a counterexample to the following classically valid inference:
. Then we would have a counterexample to the following classically valid inference:
 $ p \vee p\nvDash ^{st}_{\mathbf {X}} \neg (\neg p \vee \neg p) $
(
$ p \vee p\nvDash ^{st}_{\mathbf {X}} \neg (\neg p \vee \neg p) $
(
 ).
). -
* Assume now that
 . Then we would have a counterexample to the following classically valid inference:
. Then we would have a counterexample to the following classically valid inference:
 $\nvDash ^{st}_{\mathbf {X}}p \vee \neg p$
(
$\nvDash ^{st}_{\mathbf {X}}p \vee \neg p$
(
 ).
).
-
-
– Now, having proved the previous case, we show that
 (we leave to the reader the case
(we leave to the reader the case
 ). If it were the case that
). If it were the case that
 then we would have a counterexample to the following classically valid inference:
then we would have a counterexample to the following classically valid inference:
 $q \nvDash ^{st}_{\mathbf {X}} p \vee q$
(
$q \nvDash ^{st}_{\mathbf {X}} p \vee q$
(
 ,
,
 $v(q)=1$
).
$v(q)=1$
). -
– We show now that
 (we leave to the reader the case
(we leave to the reader the case
 ).
).-
* Assume on the contrary that
 . Then we would have a counterexample to the following classically valid inference:
. Then we would have a counterexample to the following classically valid inference:
 $\neg (p \vee \neg p) \vee q \nvDash ^{st}_{\mathbf {X}} q $
(
$\neg (p \vee \neg p) \vee q \nvDash ^{st}_{\mathbf {X}} q $
(
 ,
,
 $v(q)=0$
).
$v(q)=0$
). -
* Assume now that
 . Then we would have a counterexample to the following classically valid inference:
. Then we would have a counterexample to the following classically valid inference:
 $ \nvDash ^{st}_{\mathbf {X}} (p \vee \neg p) \vee q$
(
$ \nvDash ^{st}_{\mathbf {X}} (p \vee \neg p) \vee q$
(
 ,
,
 $v(q)=0$
).
$v(q)=0$
).
-
-
-
-
Case (2) Assume now that
 . We will show that the other operations belong to some of the truth-collapsible schemes.
. We will show that the other operations belong to some of the truth-collapsible schemes.-
• The case of conjunction:
-
– First we show that
 (we leave to the reader the case
(we leave to the reader the case
 ). Assume on the contrary that
). Assume on the contrary that
 . Then we would have a counterexample to the following classically valid inference:
. Then we would have a counterexample to the following classically valid inference:
 $\neg (p \wedge q), p \nvDash ^{st}_{\mathbf {X}} \neg q$
(
$\neg (p \wedge q), p \nvDash ^{st}_{\mathbf {X}} \neg q$
(
 $v(p)=1$
,
$v(p)=1$
,
 ).
). -
– Now, we show that
 . Assume on the contrary that
. Assume on the contrary that
 . Then we would have a counterexample to the following classically valid inference:
. Then we would have a counterexample to the following classically valid inference:
 $ \neg \neg p \nvDash ^{st}_{\mathbf {X}} p \wedge p$
(
$ \neg \neg p \nvDash ^{st}_{\mathbf {X}} p \wedge p$
(
 ).
). -
– We show now that
 (we leave to the reader the case
(we leave to the reader the case
 ).
).-
* Assume on the contrary that
 . Then we would have a counterexample to the following classically valid inference:
. Then we would have a counterexample to the following classically valid inference:
 $ p \wedge \neg p \nvDash ^{st}_{\mathbf {X}} q $
(
$ p \wedge \neg p \nvDash ^{st}_{\mathbf {X}} q $
(
 ,
,
 $v(q)=0$
).
$v(q)=0$
). -
* Assume now that
 . Then we would have a counterexample to the following classically valid inference:
. Then we would have a counterexample to the following classically valid inference:
 $\nvDash ^{st}_{\mathbf {X}} \neg (p \wedge \neg p)$
(
$\nvDash ^{st}_{\mathbf {X}} \neg (p \wedge \neg p)$
(
 ).
).
-
-
-
• The case of disjunction:
-
– First we show that
 (we leave to the reader the case
(we leave to the reader the case
 ). Assume on the contrary that
). Assume on the contrary that
 . Then we would have a counterexample to the following classically valid inference:
. Then we would have a counterexample to the following classically valid inference:
 $p \nvDash ^{st}_{\mathbf {X}} p \vee q$
(
$p \nvDash ^{st}_{\mathbf {X}} p \vee q$
(
 $v(p)=1$
,
$v(p)=1$
,
 ).
). -
– Now, we show that
 . Assume on the contrary that
. Assume on the contrary that
 . Then we would have a counterexample to the following classically valid inference:
. Then we would have a counterexample to the following classically valid inference:
 $\neg \neg p \nvDash ^{st}_{\mathbf {X}} p \vee p$
(
$\neg \neg p \nvDash ^{st}_{\mathbf {X}} p \vee p$
(
 ).
). -
– We show now that
 (we leave to the reader the case
(we leave to the reader the case
 ). Assume on the contrary that
). Assume on the contrary that
 . Then we would have a counterexample to the following classically valid inference:
. Then we would have a counterexample to the following classically valid inference:
 $\nvDash ^{st}_{\mathbf {X}} p \vee \neg p$
(
$\nvDash ^{st}_{\mathbf {X}} p \vee \neg p$
(
 ).
).
-
-
-
Case (3) Similar to the case (2), so we leave it to the reader.
Theorem A.8. Let
![]() $\mathbf {X}$
be a three-valued scheme. If
$\mathbf {X}$
be a three-valued scheme. If
![]() $\vDash ^{st}_{\mathbf {X}} \ = \ \vDash _{2}$
, then
$\vDash ^{st}_{\mathbf {X}} \ = \ \vDash _{2}$
, then
![]() $\mathbf {X}$
is Boolean normal, and either monotonic, or collapsible.
$\mathbf {X}$
is Boolean normal, and either monotonic, or collapsible.
A.3 The proofs for
 $ss$
$ss$
Lemma A.9. Let
![]() $\mathbf {X}$
be a three-valued scheme. If
$\mathbf {X}$
be a three-valued scheme. If
![]() $\mathbf {X}$
is falsity-collapsible, then
$\mathbf {X}$
is falsity-collapsible, then
![]() $\vDash ^{ss}_{\mathbf {X}} \ \subseteq \ \vDash _{2}$
.
$\vDash ^{ss}_{\mathbf {X}} \ \subseteq \ \vDash _{2}$
.
Proof. Suppose
![]() $\Gamma \nvDash _{2} \Delta $
, i.e., there is a two-valued valuation
$\Gamma \nvDash _{2} \Delta $
, i.e., there is a two-valued valuation
![]() $v$
such that
$v$
such that
![]() $v(A)=1$
and
$v(A)=1$
and
![]() $v(B)=0$
, for every
$v(B)=0$
, for every
![]() $A \in \Gamma $
and
$A \in \Gamma $
and
![]() $B \in \Delta $
. Now we will show that
$B \in \Delta $
. Now we will show that
![]() $\Gamma \nvDash ^{ss}_{\mathbf {X}}\Delta $
, i.e., that there is a three-valued valuation
$\Gamma \nvDash ^{ss}_{\mathbf {X}}\Delta $
, i.e., that there is a three-valued valuation
![]() $v^{*}$
such that
$v^{*}$
such that
![]() $v^{*}(A)=1$
and
$v^{*}(A)=1$
and
![]() , for every
, for every
![]() $A \in \Gamma $
and
$A \in \Gamma $
and
![]() $B \in \Delta $
. We take
$B \in \Delta $
. We take
![]() $v^{*}$
to be defined as follows:
$v^{*}$
to be defined as follows:
Now we show by induction on the complexity of the formula that, on the one hand, if
![]() $v(A)=0$
, then
$v(A)=0$
, then
![]() and, on the other hand, if
and, on the other hand, if
![]() $v(A)=1$
, then
$v(A)=1$
, then
![]() $v^{*}(A)=1$
.
$v^{*}(A)=1$
.
Base case: If A is a propositional letter, then it holds by definition of the valuation
![]() $v^{*}$
.
$v^{*}$
.
Inductive step: Here we need to consider three cases:
-
•
 $A = \neg B$
.
$A = \neg B$
.-
– If
 $v(\neg B)= 0$
then
$v(\neg B)= 0$
then
 $v(B)=1$
. By IH
$v(B)=1$
. By IH
 $v^{*}(B)=1$
, then since
$v^{*}(B)=1$
, then since
 $\mathbf {X}$
is falsity-collapsible
$\mathbf {X}$
is falsity-collapsible
 .
. -
– If
 $v(\neg B)= 1$
then
$v(\neg B)= 1$
then
 $v(B)= 0$
. By IH
$v(B)= 0$
. By IH
 , then since
, then since
 $\mathbf {X}$
is falsity-collapsible
$\mathbf {X}$
is falsity-collapsible
 $v^{*}(\neg B)=1$
.
$v^{*}(\neg B)=1$
.
-
-
•
 $A = B \wedge C$
.
$A = B \wedge C$
.-
– If
 $v(B \wedge C)= 0$
then
$v(B \wedge C)= 0$
then
 $v(B)=0$
or
$v(B)=0$
or
 $v(C)=0$
. By IH
$v(C)=0$
. By IH
 or
or
 , then since
, then since
 $\mathbf {X}$
is falsity-collapsible
$\mathbf {X}$
is falsity-collapsible
 .
. -
– If
 $v(B \wedge C)= 1$
then
$v(B \wedge C)= 1$
then
 $v(B)= v(C)= 1$
. Then, by IH
$v(B)= v(C)= 1$
. Then, by IH
 $v^{*}(B)= v^{*}(C)= 1$
. Thus, since
$v^{*}(B)= v^{*}(C)= 1$
. Thus, since
 $\mathbf {X}$
is falsity-collapsible
$\mathbf {X}$
is falsity-collapsible
 $v^{*}(B \wedge C)=1$
.
$v^{*}(B \wedge C)=1$
.
-
-
•
 $A = B \vee C$
.
$A = B \vee C$
.-
– If
 $v(B \vee C)= 1$
then
$v(B \vee C)= 1$
then
 $v(B)=1$
or
$v(B)=1$
or
 $v(C)=1$
. So, depending on which of these two is the case, by IH
$v(C)=1$
. So, depending on which of these two is the case, by IH
 $v^{*}(B)=1$
or
$v^{*}(B)=1$
or
 $v^{*}(C)=1$
, and then since
$v^{*}(C)=1$
, and then since
 $\mathbf {X}$
is falsity-collapsible
$\mathbf {X}$
is falsity-collapsible
 $v^{*}(B \vee C)=1$
.
$v^{*}(B \vee C)=1$
. -
– If
 $v(B \vee C)= 0$
then
$v(B \vee C)= 0$
then
 $v(B)=v(C)=0$
. By IH
$v(B)=v(C)=0$
. By IH
 and
and
 , then since
, then since
 $\mathbf {X}$
is falsity-collapsible
$\mathbf {X}$
is falsity-collapsible
 .
.
-
This shows
![]() $v^{*}$
is a three-valued valuation witnessing
$v^{*}$
is a three-valued valuation witnessing
![]() $\Gamma \nvDash ^{ss}_{\mathbf {X}} \Delta $
, and therefore that
$\Gamma \nvDash ^{ss}_{\mathbf {X}} \Delta $
, and therefore that
![]() $ \vDash ^{ss}_{\mathbf {X}} \ \subseteq \ \vDash _{2} $
as desired.
$ \vDash ^{ss}_{\mathbf {X}} \ \subseteq \ \vDash _{2} $
as desired.
Theorem A.10. Let
![]() $\mathbf {X}$
be a three-valued scheme. If
$\mathbf {X}$
be a three-valued scheme. If
![]() $\mathbf {X}$
is falsity-collapsible, then
$\mathbf {X}$
is falsity-collapsible, then
![]() $\vDash ^{ss}_{\mathbf {X}} \ = \ \vDash _{2}$
.
$\vDash ^{ss}_{\mathbf {X}} \ = \ \vDash _{2}$
.
Theorem A.11. Let
![]() $\mathbf {X}$
be a three-valued scheme. If
$\mathbf {X}$
be a three-valued scheme. If
![]() $\vDash ^{ss}_{\mathbf {X}} \ = \ \vDash _{2}$
, then
$\vDash ^{ss}_{\mathbf {X}} \ = \ \vDash _{2}$
, then
![]() $\mathbf {X}$
is falsity-collapsible
$\mathbf {X}$
is falsity-collapsible
![]() $($
i.e., the operations are those of the schemes in Figure 6
$($
i.e., the operations are those of the schemes in Figure 6
![]() $)$
.
$)$
.
Proof. We will show that if a three-valued scheme
![]() $\mathbf {X}$
is not falsity-collapsible then
$\mathbf {X}$
is not falsity-collapsible then
![]() $\ \vDash _{2}\ \nsubseteq \vDash ^{ss}_{\mathbf {X}} $
. We will show it by cases, considering in order each of the connectives of each possible non-falsity-collapsible scheme.
$\ \vDash _{2}\ \nsubseteq \vDash ^{ss}_{\mathbf {X}} $
. We will show it by cases, considering in order each of the connectives of each possible non-falsity-collapsible scheme.
-
• The case of negation:
-
1. Assume
 $\mathbf {X}$
is such that
$\mathbf {X}$
is such that
 $\neg 1 = 1$
. Then,
$\neg 1 = 1$
. Then,
 $ p, \neg p \nvDash ^{ss}_{\mathbf {X}} q$
, but of course
$ p, \neg p \nvDash ^{ss}_{\mathbf {X}} q$
, but of course
 $p, \neg p \vDash _{2} q$
.
$p, \neg p \vDash _{2} q$
. -
2. Assume
 $\mathbf {X}$
is such that
$\mathbf {X}$
is such that
 . Then,
. Then,
 $ q \nvDash ^{ss}_{\mathbf {X}} p, \neg p$
, but of course
$ q \nvDash ^{ss}_{\mathbf {X}} p, \neg p$
, but of course
 $q \vDash _{2} p, \neg p$
.
$q \vDash _{2} p, \neg p$
. -
3. Assume
 $\mathbf {X}$
is such that
$\mathbf {X}$
is such that
 $\neg 0 \neq 1$
. Then,
$\neg 0 \neq 1$
. Then,
 $ q \nvDash ^{ss}_{\mathbf {X}} p, \neg p$
, but of course
$ q \nvDash ^{ss}_{\mathbf {X}} p, \neg p$
, but of course
 $q \vDash _{2} p, \neg p$
.
$q \vDash _{2} p, \neg p$
.
-
-
• The case of conjunction:
-
1. Assume
 $\mathbf {X}$
is such that
$\mathbf {X}$
is such that
 $x \wedge y \neq 1$
, for
$x \wedge y \neq 1$
, for
 $x=1$
and
$x=1$
and
 $y=1$
. Then,
$y=1$
. Then,
 $ p, q \nvDash ^{ss}_{\mathbf {X}}p \wedge q$
, but of course
$ p, q \nvDash ^{ss}_{\mathbf {X}}p \wedge q$
, but of course
 $ p, q \vDash _{2}p \wedge q$
.
$ p, q \vDash _{2}p \wedge q$
. -
2. Assume
 $\mathbf {X}$
is such that
$\mathbf {X}$
is such that
 $x \wedge y = 1$
, for
$x \wedge y = 1$
, for
 $x\neq 1$
. Then,
$x\neq 1$
. Then,
 $ p \wedge q \nvDash ^{ss}_{\mathbf {X}} p$
, but of course
$ p \wedge q \nvDash ^{ss}_{\mathbf {X}} p$
, but of course
 $ p \wedge q \vDash _{2} p$
.
$ p \wedge q \vDash _{2} p$
. -
3. Assume
 $\mathbf {X}$
is such that
$\mathbf {X}$
is such that
 $x \wedge y = 1$
, for
$x \wedge y = 1$
, for
 $y\neq 1$
. Then,
$y\neq 1$
. Then,
 $ p \wedge q \nvDash ^{ss}_{\mathbf {X}} q$
, but of course
$ p \wedge q \nvDash ^{ss}_{\mathbf {X}} q$
, but of course
 $ p \wedge q \vDash _{2} q$
.
$ p \wedge q \vDash _{2} q$
.
-
-
• The case of disjunction:
-
1. Assume
 $\mathbf {X}$
is such that
$\mathbf {X}$
is such that
 $x \vee y \neq 1$
, for
$x \vee y \neq 1$
, for
 $x= 1$
. Then,
$x= 1$
. Then,
 $ p \nvDash ^{ss}_{\mathbf {X}} p \vee q$
, but of course
$ p \nvDash ^{ss}_{\mathbf {X}} p \vee q$
, but of course
 $ p \vDash _{2} p \vee q$
.
$ p \vDash _{2} p \vee q$
. -
2. Assume
 $\mathbf {X}$
is such that
$\mathbf {X}$
is such that
 $x \vee y \neq 1$
, for
$x \vee y \neq 1$
, for
 $y= 1$
. Then,
$y= 1$
. Then,
 $ q \nvDash ^{ss}_{\mathbf {X}} p \vee q$
, but of course
$ q \nvDash ^{ss}_{\mathbf {X}} p \vee q$
, but of course
 $ q \vDash _{2}p \vee q$
.
$ q \vDash _{2}p \vee q$
. -
3. Assume
 $\mathbf {X}$
is such that
$\mathbf {X}$
is such that
 $x \vee y = 1$
, for
$x \vee y = 1$
, for
 $x \neq 1$
and
$x \neq 1$
and
 $y \neq 1$
. Then,
$y \neq 1$
. Then,
 $ p \vee q \nvDash ^{ss}_{\mathbf {X}} p, q$
, but of course
$ p \vee q \nvDash ^{ss}_{\mathbf {X}} p, q$
, but of course
 $ p \vee q \vDash _{2} p, q$
. here
$ p \vee q \vDash _{2} p, q$
. here
-
A.4 The proofs for
 $tt$
$tt$
We omit all the proofs of this section, since basically they are dual to those for
![]() $ss$
.
$ss$
.
Lemma A.12. Let
![]() $\mathbf {X}$
be a three-valued scheme. If
$\mathbf {X}$
be a three-valued scheme. If
![]() $\mathbf {X}$
is truth-collapsible, then
$\mathbf {X}$
is truth-collapsible, then
![]() $\vDash ^{tt}_{\mathbf {X}} \ \subseteq \ \vDash _{2}$
.
$\vDash ^{tt}_{\mathbf {X}} \ \subseteq \ \vDash _{2}$
.
Theorem A.13. Let
![]() $\mathbf {X}$
be a three-valued scheme. If
$\mathbf {X}$
be a three-valued scheme. If
![]() $\mathbf {X}$
is truth-collapsible, then
$\mathbf {X}$
is truth-collapsible, then
![]() $\vDash ^{tt}_{\mathbf {X}} \ = \ \vDash _{2}$
.
$\vDash ^{tt}_{\mathbf {X}} \ = \ \vDash _{2}$
.
Theorem A.14. Let
![]() $\mathbf {X}$
be a three-valued scheme. If
$\mathbf {X}$
be a three-valued scheme. If
![]() $\vDash ^{tt}_{\mathbf {X}} \ = \ \vDash _{2}$
, then
$\vDash ^{tt}_{\mathbf {X}} \ = \ \vDash _{2}$
, then
![]() $\mathbf {X}$
is truth-collapsible
$\mathbf {X}$
is truth-collapsible
![]() $($
i.e., the operations are those of the schemes in Figure 5
$($
i.e., the operations are those of the schemes in Figure 5
![]() $)$
.
$)$
.
B Gentzen-regularity and classical logic
Following [Reference Chemla and Égré6], we call a connective Gentzen-regular if its behavior, whether in the conclusions or in the premises of an argument, can be explained fully in terms of conjunction of sequents involving the subformulae related by that connective. Formally, the definition is the following:
Definition B.1 (Gentzen-regular connectives)
Given a consequence relation
![]() $\vdash $
, an n-ary connective C (for
$\vdash $
, an n-ary connective C (for
![]() $n\geq 0$
) is Gentzen-regular for it if there exist
$n\geq 0$
) is Gentzen-regular for it if there exist
![]() $\mathcal {B}^p\subseteq \mathcal {P}(\{1,..., n\})\times \mathcal {P}(\{1,..., n\})$
and
$\mathcal {B}^p\subseteq \mathcal {P}(\{1,..., n\})\times \mathcal {P}(\{1,..., n\})$
and
![]() $\mathcal {B}^c\subseteq \mathcal {P}(\{1,..., n\})\times \mathcal {P}(\{1,..., n\})$
such that
$\mathcal {B}^c\subseteq \mathcal {P}(\{1,..., n\})\times \mathcal {P}(\{1,..., n\})$
such that
![]() $\forall \Gamma , \Delta , \forall F_1, ..., F_n:$
$\forall \Gamma , \Delta , \forall F_1, ..., F_n:$
 $$\begin{align*}\begin{array}{c@{\textrm{ iff }}c} \Gamma, C(F_1, ..., F_n) \vdash \Delta & \bigwedge\limits_{(B_p,B_c)\in \mathcal{B}^p} {\Gamma, \{F_i: i\in B_p\}\vdash \{F_i: i\in B_c\}, \Delta}\\ \Gamma \vdash C(F_1, ..., F_n) , \Delta & \bigwedge\limits_{(B_p,B_c)\in \mathcal{B}^c} {\Gamma, \{F_i: i\in B_p\}\vdash \{F_i: i\in B_c\}, \Delta}\\ \end{array}\end{align*}$$
$$\begin{align*}\begin{array}{c@{\textrm{ iff }}c} \Gamma, C(F_1, ..., F_n) \vdash \Delta & \bigwedge\limits_{(B_p,B_c)\in \mathcal{B}^p} {\Gamma, \{F_i: i\in B_p\}\vdash \{F_i: i\in B_c\}, \Delta}\\ \Gamma \vdash C(F_1, ..., F_n) , \Delta & \bigwedge\limits_{(B_p,B_c)\in \mathcal{B}^c} {\Gamma, \{F_i: i\in B_p\}\vdash \{F_i: i\in B_c\}, \Delta}\\ \end{array}\end{align*}$$
The next lemma relates this feature of the connectives, what it is for a logic to be classical, and a structural condition on sets of atomic propositions (atom-sharing between premises and conclusions).
Lemma B.2. A propositional logic
![]() $L=\langle {\mathcal {L}}, \vdash , C\rangle $
is inferentially classical if and only if its connectives in C are Gentzen-regular and
$L=\langle {\mathcal {L}}, \vdash , C\rangle $
is inferentially classical if and only if its connectives in C are Gentzen-regular and
![]() $\vdash $
is such that for
$\vdash $
is such that for
![]() $\Gamma $
and
$\Gamma $
and
![]() $\Delta $
any two sets of atomic propositions,
$\Delta $
any two sets of atomic propositions,
![]() $\Gamma \vdash \Delta $
iff
$\Gamma \vdash \Delta $
iff
![]() $\Gamma \cap \Delta \neq \emptyset $
.
$\Gamma \cap \Delta \neq \emptyset $
.
Proof. The left-to-right direction holds because in classical logic, and in any logic that satisfies the same inferences, connectives are Gentzen-regular, and inferences involving only atomic propositions behave as described.
Conversely, suppose the right-hand-side holds for a logic L. Consider then sets of premises and conclusions
![]() $\Gamma $
and
$\Gamma $
and
![]() $\Delta $
. If
$\Delta $
. If
![]() $\Gamma $
and
$\Gamma $
and
![]() $\Delta $
only contain atomic propositions, then
$\Delta $
only contain atomic propositions, then
![]() $\Gamma \vdash \Delta $
holds in L iff
$\Gamma \vdash \Delta $
holds in L iff
![]() $\Gamma \cap \Delta \neq \emptyset $
, by hypothesis, iff it holds in classical logic then.
$\Gamma \cap \Delta \neq \emptyset $
, by hypothesis, iff it holds in classical logic then.
By induction on the complexity of the formulae involved, the assumption of Gentzen-regularity allows us to generalize this equivalence between L and classical logic to inferences with non-atomic propositions. Indeed, the Gentzen regularity rules reduce the validity of any inference
![]() $\Gamma \vdash \Delta $
to the validity of a conjunction of inferences involving formulae of strictly lower syntactic complexity.Footnote
10
$\Gamma \vdash \Delta $
to the validity of a conjunction of inferences involving formulae of strictly lower syntactic complexity.Footnote
10
For concreteness, consider
![]() $\Gamma ', A\vee B\vdash \Delta $
. This holds if and only if both
$\Gamma ', A\vee B\vdash \Delta $
. This holds if and only if both
![]() $\Gamma ', A\vdash \Delta $
and
$\Gamma ', A\vdash \Delta $
and
![]() $\Gamma ', B\vdash \Delta $
hold. This shows how the Gentzen premise-rule reduces the verification of inferences with disjunction in premises, to the verification of strictly simpler inferences, with no disjunctions in premises. Eliminating connectives one after the other thanks to Gentzen rules, in premises and in conclusion, we can recursively reduce the complexity of the inferences until no more reduction is possible. That is, we can find sets of atomic propositions
$\Gamma ', B\vdash \Delta $
hold. This shows how the Gentzen premise-rule reduces the verification of inferences with disjunction in premises, to the verification of strictly simpler inferences, with no disjunctions in premises. Eliminating connectives one after the other thanks to Gentzen rules, in premises and in conclusion, we can recursively reduce the complexity of the inferences until no more reduction is possible. That is, we can find sets of atomic propositions
![]() $\Gamma _i, \Delta _i$
such that
$\Gamma _i, \Delta _i$
such that
![]() $\Gamma \vdash \Delta $
holds if and only if the conjunction of the
$\Gamma \vdash \Delta $
holds if and only if the conjunction of the
![]() $\Gamma _i\vdash \Delta _i$
holds.
$\Gamma _i\vdash \Delta _i$
holds.
Three remarks may be made about this result. The first is that a logic can obey the conditions of Lemma B.2 without coinciding exactly with classical logic. For instance, if
![]() $C=\{\neg , \leftrightarrow \}$
, with
$C=\{\neg , \leftrightarrow \}$
, with
![]() $\neg $
and
$\neg $
and
![]() $\leftrightarrow $
obeying the expected Gentzen rules, then the resulting logic is inferentially classical but is only a fragment of classical logic (because it is functionally incomplete). The second is that irrespective of how Gentzen-regular connectives are named in
$\leftrightarrow $
obeying the expected Gentzen rules, then the resulting logic is inferentially classical but is only a fragment of classical logic (because it is functionally incomplete). The second is that irrespective of how Gentzen-regular connectives are named in
![]() $\mathcal {L}$
, what matters concerns which operations they correspond to. To use the same example as in the proof, if
$\mathcal {L}$
, what matters concerns which operations they correspond to. To use the same example as in the proof, if
![]() $\Gamma ', A\wedge B\vdash \Delta $
holds iff
$\Gamma ', A\wedge B\vdash \Delta $
holds iff
![]() $\Gamma ', A\vdash \Delta $
and
$\Gamma ', A\vdash \Delta $
and
![]() $\Gamma ', B\vdash \Delta $
hold in
$\Gamma ', B\vdash \Delta $
hold in
![]() $\mathcal {L}$
, then it means that “
$\mathcal {L}$
, then it means that “
![]() $\wedge $
” is actually just another name for disjunction in that logic. The third finally is that the structural condition in the lemma simply corresponds to a form of (strong) Reflexivity on the atoms. It can be verified that it directly implies the admissibility of other classical structural rules, including Exchange, Contraction, Weakening, and Cut, for sequents involving only atoms. For example, if
$\wedge $
” is actually just another name for disjunction in that logic. The third finally is that the structural condition in the lemma simply corresponds to a form of (strong) Reflexivity on the atoms. It can be verified that it directly implies the admissibility of other classical structural rules, including Exchange, Contraction, Weakening, and Cut, for sequents involving only atoms. For example, if
![]() $\Gamma , \Gamma ', \Delta , \Delta '$
are sets of atoms, then it follows that
$\Gamma , \Gamma ', \Delta , \Delta '$
are sets of atoms, then it follows that
![]() $\Gamma \vdash \Delta , p$
and
$\Gamma \vdash \Delta , p$
and
![]() $\Gamma ', p\vdash \Delta '$
imply
$\Gamma ', p\vdash \Delta '$
imply
![]() $\Gamma , \Gamma '\vdash \Delta , \Delta '$
.
$\Gamma , \Gamma '\vdash \Delta , \Delta '$
.
C Monotonic operators
Fact C.1. Given a truth table for a unary or binary operator f, the operator is monotonic only if no two horizontally or vertically adjacent cells of the corresponding matrix contain a 1 and a 0.
Proof. In the unary case, suppose as a particular case that
![]() $f(1/2)=0$
and
$f(1/2)=0$
and
![]() $f(1)=1$
. Then, although
$f(1)=1$
. Then, although
![]() $1/2<_{\mathrm I}1$
, their images by f are incomparable. The other cases are symmetric. In the binary case, suppose as a particular case of vertical adjacent cells that
$1/2<_{\mathrm I}1$
, their images by f are incomparable. The other cases are symmetric. In the binary case, suppose as a particular case of vertical adjacent cells that
![]() $f(1/2,1)=0$
when
$f(1/2,1)=0$
when
![]() $f(0,1)=1$
. Then although
$f(0,1)=1$
. Then although
![]() $(1/2,1)<^{comp}_{\mathrm I}(0,1)$
, their images by f are incomparable, which violates monotonicity. The other cases are symmetric.
$(1/2,1)<^{comp}_{\mathrm I}(0,1)$
, their images by f are incomparable, which violates monotonicity. The other cases are symmetric.
Fact C.2. A binary normal Boolean operator
![]() $f$
is monotonic if and only if no two adjacent cells of its matrix get values
$f$
is monotonic if and only if no two adjacent cells of its matrix get values
![]() $1$
and
$1$
and
![]() $0$
and if
$0$
and if
![]() $f(1/2,1/2)$
is not greater than or incomparable with the value of any other cell.
$f(1/2,1/2)$
is not greater than or incomparable with the value of any other cell.
Proof. From left-to-right, suppose that
![]() $f(1/2,1/2)$
is incomparable with or greater than the value of some other cell. Since
$f(1/2,1/2)$
is incomparable with or greater than the value of some other cell. Since
![]() $(1/2,1/2)<^{comp}_{\mathrm I}(x,y)$
for all other cells
$(1/2,1/2)<^{comp}_{\mathrm I}(x,y)$
for all other cells
![]() $(x,y)$
, this violates monotonicity. The other condition is entailed by Fact C.1.
$(x,y)$
, this violates monotonicity. The other condition is entailed by Fact C.1.
From right-to-left, suppose that f is normal but not monotonic. Then there exist
![]() $(x,y)\leq ^{comp}_{\mathrm I} (x',y')$
, but either
$(x,y)\leq ^{comp}_{\mathrm I} (x',y')$
, but either
![]() $f(x,y)\geq ^{comp}_{\mathrm I}f(x',y')$
, or
$f(x,y)\geq ^{comp}_{\mathrm I}f(x',y')$
, or
![]() $f(x,y)$
and
$f(x,y)$
and
![]() $f(x',y')$
are incomparable. If
$f(x',y')$
are incomparable. If
![]() $(x,y)$
is of type
$(x,y)$
is of type
![]() $(c,1/2)$
or
$(c,1/2)$
or
![]() $(1/2,c)$
with c classical, and
$(1/2,c)$
with c classical, and
![]() $(x',y')$
of type
$(x',y')$
of type
![]() $(c,c)$
, then necessarily one of them is 1 and the other 0. If
$(c,c)$
, then necessarily one of them is 1 and the other 0. If
![]() $(x,y)$
is
$(x,y)$
is
![]() $(1/2, 1/2)$
, then the violation is necessary because
$(1/2, 1/2)$
, then the violation is necessary because
![]() $f(x,y)=c$
and
$f(x,y)=c$
and
![]() $f(x',y')$
is
$f(x',y')$
is
![]() $1/2$
or incomparable.
$1/2$
or incomparable.
Acknowledgments
We acknowledge Rohan French (our Editor) and two anonymous referees for detailed and very helpful comments. We are grateful to a referee for catching and allowing us to correct a mistake in a definition. Thanks also to the members of the Buenos Aires Logic Group for very helpful feedback on earlier versions of this paper, and to several audiences, in particular at the 2021 Navarra workshop on logical consequence held in Pamplona.
Funding
The authors received support from the French programs ANR-17-EURE0017 (FrontCog) and ANR-19-CE28-0019-01 (Ambisense), and from PLEXUS (grant agreement no. 101086295), a Marie Skłodowska-Curie action funded by the EU under the Horizon Europe Research and Innovation Programme. BDR acknowledges a postdoctoral scholarship from CONICET during the time this paper was written.
Author contributions
This collaboration was initiated during a visit of DS to ENS Paris in 2020, based on preliminary findings by BDR and DS. All four authors contributed substantially to the results, writing, and shape of this paper.
Conflict of interest
The authors declare no conflict of interest.