For a graph 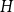$H$ and a hypercube 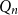$Q_n$, 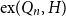$\textrm{ex}(Q_n, H)$ is the largest number of edges in an 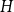$H$-free subgraph of 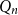$Q_n$. If 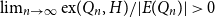$\lim _{n \rightarrow \infty } \textrm{ex}(Q_n, H)/|E(Q_n)| \gt 0$, 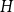$H$ is said to have a positive Turán density in a hypercube or simply a positive Turán density; otherwise, it has zero Turán density. Determining 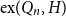$\textrm{ex}(Q_n, H)$ and even identifying whether 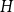$H$ has a positive or zero Turán density remains a widely open question for general 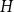$H$. By relating extremal numbers in a hypercube and certain corresponding hypergraphs, Conlon found a large class of graphs, ones having so-called partite representation, that have zero Turán density. He asked whether this gives a characterisation, that is, whether a graph has zero Turán density if and only if it has partite representation. Here, we show that, as suspected by Conlon, this is not the case. We give an example of a class of graphs which have no partite representation, but on the other hand, have zero Turán density. In addition, we show that any graph whose every block has partite representation has zero Turán density in a hypercube.

We consider subgraph counts in general preferential attachment models with power-law degree exponent $\tau > 2$. For all subgraphs H, we find the scaling of the expected number of subgraphs as a power of the number of vertices. We prove our results on the expected number of subgraphs by defining an optimization problem that finds the optimal subgraph structure in terms of the indices of the vertices that together span it and by using the representation of the preferential attachment model as a Pólya urn model.