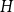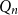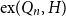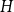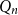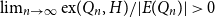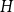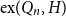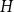1. Introduction
A hypercube
![]() $Q_n$
with a ground set
$Q_n$
with a ground set
![]() $X$
of size
$X$
of size
![]() $n$
is a graph on a vertex set
$n$
is a graph on a vertex set
![]() $\{A\,:\, A\subseteq X\}$
and an edge set consisting of all pairs
$\{A\,:\, A\subseteq X\}$
and an edge set consisting of all pairs
![]() $\{A,B\}$
, where
$\{A,B\}$
, where
![]() $A\subseteq B$
and
$A\subseteq B$
and
![]() $|A|=|B|-1$
. Unless specified,
$|A|=|B|-1$
. Unless specified,
![]() $X=[n]$
, where
$X=[n]$
, where
![]() $[n]= \{1, \ldots, n\}$
. We often identify vertices of
$[n]= \{1, \ldots, n\}$
. We often identify vertices of
![]() $Q_n$
with binary vectors that are indicator vectors of respective sets. If a graph is a subgraph of
$Q_n$
with binary vectors that are indicator vectors of respective sets. If a graph is a subgraph of
![]() $Q_n$
, for some
$Q_n$
, for some
![]() $n$
, it is called cubical. We denote the number of vertices and the number of edges in a graph
$n$
, it is called cubical. We denote the number of vertices and the number of edges in a graph
![]() $H$
by
$H$
by
![]() $|H|$
and
$|H|$
and
![]() $||H||$
, respectively. The degree of a vertex
$||H||$
, respectively. The degree of a vertex
![]() $y$
in a graph
$y$
in a graph
![]() $H$
is denoted
$H$
is denoted
![]() $d(y)$
or
$d(y)$
or
![]() $d_H(y)$
. A block in a graph is a maximal connected subgraph without a cut-vertex. Note that two distinct blocks in a graph share at most one vertex. We shall need the notion of layers. The
$d_H(y)$
. A block in a graph is a maximal connected subgraph without a cut-vertex. Note that two distinct blocks in a graph share at most one vertex. We shall need the notion of layers. The
![]() $i$
th vertex layer of
$i$
th vertex layer of
![]() $Q_n$
, denoted
$Q_n$
, denoted
![]() $V_i$
, is the set of vertices
$V_i$
, is the set of vertices
![]() $\binom{[n]}{i}$
,
$\binom{[n]}{i}$
,
![]() $i=0, \ldots, n$
. The
$i=0, \ldots, n$
. The
![]() $i$
th edge layer
$i$
th edge layer
![]() $L_i$
of
$L_i$
of
![]() $Q_n$
is a graph induced by
$Q_n$
is a graph induced by
![]() $V_i\cup V_{i-1}$
,
$V_i\cup V_{i-1}$
,
![]() $i\in [n]$
. A cycle of length
$i\in [n]$
. A cycle of length
![]() $n$
is denoted by
$n$
is denoted by
![]() $C_n$
.
$C_n$
.
For a graph
![]() $H$
, let the extremal number of
$H$
, let the extremal number of
![]() $H$
in
$H$
in
![]() $Q_n$
, denoted
$Q_n$
, denoted
![]() $\textrm{ex}(Q_n, H)$
, be the largest number of edges in a subgraph
$\textrm{ex}(Q_n, H)$
, be the largest number of edges in a subgraph
![]() $G$
of
$G$
of
![]() $Q_n$
such that there is no subgraph of
$Q_n$
such that there is no subgraph of
![]() $G$
isomorphic to
$G$
isomorphic to
![]() $H$
. A graph
$H$
. A graph
![]() $H$
is said to have zero Turán density in a hypercube if
$H$
is said to have zero Turán density in a hypercube if
![]() $\textrm{ex}(Q_n, H) = o(||Q_n||)$
. Otherwise, we say that
$\textrm{ex}(Q_n, H) = o(||Q_n||)$
. Otherwise, we say that
![]() $H$
has a positive Turán density in a hypercube. Note that by using a standard double counting argument, the sequence
$H$
has a positive Turán density in a hypercube. Note that by using a standard double counting argument, the sequence
![]() $\textrm{ex}(Q_n, H)/||Q_n||$
is non-increasing; thus, the above density notions are well defined. When clear from context, we simply say Turán density instead of Turán density in a hypercube. The behaviour of the function
$\textrm{ex}(Q_n, H)/||Q_n||$
is non-increasing; thus, the above density notions are well defined. When clear from context, we simply say Turán density instead of Turán density in a hypercube. The behaviour of the function
![]() $\textrm{ex}(Q_n, H)$
is not well understood in general, and it is not even known what graphs have positive or zero Turán density. Currently, the only known cubical graphs of positive Turán density are those containing
$\textrm{ex}(Q_n, H)$
is not well understood in general, and it is not even known what graphs have positive or zero Turán density. Currently, the only known cubical graphs of positive Turán density are those containing
![]() $C_4$
or
$C_4$
or
![]() $C_6$
as a subgraph, [Reference Chung8, Reference Conder9], and one special graph of girth
$C_6$
as a subgraph, [Reference Chung8, Reference Conder9], and one special graph of girth
![]() $8$
[Reference Axenovich, Martin and Winter2]. Conlon [Reference Conlon10] observed a connection between extremal numbers in a hypercube and classical extremal numbers for uniform hypergraphs. This connection proved that graphs in a large class, including some subdivisions, have zero Turán density, see [Reference Axenovich, Martin and Winter2]. For more results on extremal numbers in a hypercube, see [Reference Alon, Krech and Szabó1, Reference Baber5, Reference Balogh, Hu, Lidický and Liu6, Reference Offner16, Reference Thomason and Wagner17].
$8$
[Reference Axenovich, Martin and Winter2]. Conlon [Reference Conlon10] observed a connection between extremal numbers in a hypercube and classical extremal numbers for uniform hypergraphs. This connection proved that graphs in a large class, including some subdivisions, have zero Turán density, see [Reference Axenovich, Martin and Winter2]. For more results on extremal numbers in a hypercube, see [Reference Alon, Krech and Szabó1, Reference Baber5, Reference Balogh, Hu, Lidický and Liu6, Reference Offner16, Reference Thomason and Wagner17].
A graph
![]() $H$
has a
$H$
has a
![]() $k$
-partite representation
$k$
-partite representation
![]() $\mathcal{H}$
, where
$\mathcal{H}$
, where
![]() $\mathcal{H}$
is
$\mathcal{H}$
is
![]() $k$
-partite
$k$
-partite
![]() $k$
-uniform hypergraph, if for some
$k$
-uniform hypergraph, if for some
![]() $n$
,
$n$
,
![]() $H$
is isomorphic to a subgraph
$H$
is isomorphic to a subgraph
![]() $H^{\prime}$
of the
$H^{\prime}$
of the
![]() $k$
th layer
$k$
th layer
![]() $L_k$
of
$L_k$
of
![]() $Q_n$
such that
$Q_n$
such that
![]() $V(H^{\prime}) \cap V_k$
is an edge set of
$V(H^{\prime}) \cap V_k$
is an edge set of
![]() $\mathcal{H}$
. The graph
$\mathcal{H}$
. The graph
![]() $H^{\prime}$
is called a representing graph. If
$H^{\prime}$
is called a representing graph. If
![]() $H$
has a
$H$
has a
![]() $k$
-partite representation for some
$k$
-partite representation for some
![]() $k$
, we say that
$k$
, we say that
![]() $H$
has a partite representation. Here, a
$H$
has a partite representation. Here, a
![]() $k$
-uniform hypergraph is
$k$
-uniform hypergraph is
![]() $k$
-partite if the vertex set can be partitioned into
$k$
-partite if the vertex set can be partitioned into
![]() $k$
parts such that each hyperedge has exactly one vertex in each part. Here, we omit the brackets and commas denoting sets, when clear from context, that is, for a set
$k$
parts such that each hyperedge has exactly one vertex in each part. Here, we omit the brackets and commas denoting sets, when clear from context, that is, for a set
![]() $\{1,2\}$
we simply write
$\{1,2\}$
we simply write
![]() $12$
. For example, if
$12$
. For example, if
![]() $H=C_8$
, it has a
$H=C_8$
, it has a
![]() $2$
-partite representation
$2$
-partite representation
![]() $\mathcal{H}$
with hyperedges
$\mathcal{H}$
with hyperedges
![]() $12, 23, 34, 14$
corresponding to an
$12, 23, 34, 14$
corresponding to an
![]() $C_8$
with vertices
$C_8$
with vertices
![]() $1, 12, 2, 23, 3, 34, 4, 14, 1$
, in order. For a
$1, 12, 2, 23, 3, 34, 4, 14, 1$
, in order. For a
![]() $k$
-uniform hypergraph
$k$
-uniform hypergraph
![]() $\mathcal{H}$
,
$\mathcal{H}$
,
![]() $\textrm{ex}_k(n, \mathcal{H})$
denotes the largest number of edges in a
$\textrm{ex}_k(n, \mathcal{H})$
denotes the largest number of edges in a
![]() $k$
-uniform
$k$
-uniform
![]() $n$
-vertex hypergraph with no subgraph isomorphic to
$n$
-vertex hypergraph with no subgraph isomorphic to
![]() $\mathcal{H}$
.
$\mathcal{H}$
.
Using a theorem by Erdős [Reference Erdős11], that states that
![]() $\textrm{ex}_k(n, \mathcal{H}) = o_n(n^k)$
for any
$\textrm{ex}_k(n, \mathcal{H}) = o_n(n^k)$
for any
![]() $k$
-partite hypergraph
$k$
-partite hypergraph
![]() $\mathcal{H}$
, Conlon [Reference Conlon10] proved that if a graph
$\mathcal{H}$
, Conlon [Reference Conlon10] proved that if a graph
![]() $H$
has partite representation, then
$H$
has partite representation, then
![]() $\textrm{ex}(Q_n, H) = o(||Q_n||)$
. In the same paper, Conlon [Reference Conlon10] asked whether cubical graphs that have no partite representation have positive Turán density. Here, we show that it is not the case, that is, having a partite representation is not a characterisation for zero Turán density in a hypercube. For that, we construct a family of cubical graphs that have no partite representation but have zero Turán density. These graphs are formed by two copies of so-called theta-graphs that we define below.
$\textrm{ex}(Q_n, H) = o(||Q_n||)$
. In the same paper, Conlon [Reference Conlon10] asked whether cubical graphs that have no partite representation have positive Turán density. Here, we show that it is not the case, that is, having a partite representation is not a characterisation for zero Turán density in a hypercube. For that, we construct a family of cubical graphs that have no partite representation but have zero Turán density. These graphs are formed by two copies of so-called theta-graphs that we define below.
For a graph
![]() $G$
, let
$G$
, let
![]() $G(1)$
be a
$G(1)$
be a
![]() $1$
-subdivision of
$1$
-subdivision of
![]() $G$
, that is, a graph
$G$
, that is, a graph
![]() $G^{\prime}$
with a vertex set
$G^{\prime}$
with a vertex set
![]() $V(G) \cup E(G)$
and an edge set
$V(G) \cup E(G)$
and an edge set
![]() $\{ue, ev\,:\, e=uv\in E(G)\}$
. We call the vertices from
$\{ue, ev\,:\, e=uv\in E(G)\}$
. We call the vertices from
![]() $V(G)$
in
$V(G)$
in
![]() $G^{\prime}$
, the poles of
$G^{\prime}$
, the poles of
![]() $G^{\prime}$
and other vertices, the subdivision vertices. Let
$G^{\prime}$
and other vertices, the subdivision vertices. Let
![]() $K_{s,t}$
denote a complete bipartite graph with parts of sizes
$K_{s,t}$
denote a complete bipartite graph with parts of sizes
![]() $s$
and
$s$
and
![]() $t$
, respectively. We shall be considering the
$t$
, respectively. We shall be considering the
![]() $1$
-subdivision of
$1$
-subdivision of
![]() $K_{q,2}$
,
$K_{q,2}$
,
![]() $q\geq 3$
. We shall call the two vertices of degree
$q\geq 3$
. We shall call the two vertices of degree
![]() $q$
in
$q$
in
![]() $K_{q, 2}(1)$
, the main poles. Note that
$K_{q, 2}(1)$
, the main poles. Note that
![]() $K_{q,2}(1)$
is also referred to as a theta graph with
$K_{q,2}(1)$
is also referred to as a theta graph with
![]() $q$
legs of length
$q$
legs of length
![]() $4$
. Here, the legs are paths with end points being main poles. We shall use a shorter notation
$4$
. Here, the legs are paths with end points being main poles. We shall use a shorter notation
![]() $\Theta (q)$
for
$\Theta (q)$
for
![]() $K_{q, 2}(1)$
, when appropriate. If a graph
$K_{q, 2}(1)$
, when appropriate. If a graph
![]() $G$
contains a subgraph isomorphic to
$G$
contains a subgraph isomorphic to
![]() $H$
, we call such a subgraph a copy of
$H$
, we call such a subgraph a copy of
![]() $H$
.
$H$
.
A characterisation by Havel and Moravek [Reference Havel and Morávek14] states that a graph is cubical if and only if it has a nice edge-colouring. Here, an edge-colouring is nice if any cycle uses each colour an even number of times and each nontrivial path uses some colour an odd number of times.
Let
![]() $H(q)$
be a union of two copies of
$H(q)$
be a union of two copies of
![]() $\Theta (q)$
sharing exactly one vertex that is a main pole of one copy and a subdivision vertex in another copy, see Fig. 1.
$\Theta (q)$
sharing exactly one vertex that is a main pole of one copy and a subdivision vertex in another copy, see Fig. 1.

Figure 1. A graph
![]() $H(3)$
with the grey vertex being a main pole of the top theta graph and a subdivision vertex the bottom theta graph. The labelling of the edges and a corresponding colouring is a nice edge-colouring of one theta graph. Larger vertices correspond to the poles.
$H(3)$
with the grey vertex being a main pole of the top theta graph and a subdivision vertex the bottom theta graph. The labelling of the edges and a corresponding colouring is a nice edge-colouring of one theta graph. Larger vertices correspond to the poles.
Marquardt [Reference Marquardt15] showed that
![]() $H(q)$
has no partite representation for
$H(q)$
has no partite representation for
![]() $q=3$
. Here, we give a slightly different proof of this fact for any
$q=3$
. Here, we give a slightly different proof of this fact for any
![]() $q\geq 3$
and show that
$q\geq 3$
and show that
![]() $H(q)$
has zero Turán density. In doing so, we prove a result of an independent interest that gives a new class of cubical graphs of zero Turán density. Note that this class contains all previously known graphs of zero Turán density, as well as new such graphs.
$H(q)$
has zero Turán density. In doing so, we prove a result of an independent interest that gives a new class of cubical graphs of zero Turán density. Note that this class contains all previously known graphs of zero Turán density, as well as new such graphs.
Theorem 1.
Let
![]() $H$
be a graph whose every block has a partite representation. Then
$H$
be a graph whose every block has a partite representation. Then
![]() $H$
has zero Turán density in a hypercube.
$H$
has zero Turán density in a hypercube.
Theorem 2.
For any
![]() $q\geq 3$
the graph
$q\geq 3$
the graph
![]() $H(q)$
is cubical, has no partite representation, but has zero Turán density in a hypercube.
$H(q)$
is cubical, has no partite representation, but has zero Turán density in a hypercube.
2. Proofs of main results
We shall need the following lemmas. Lemma 3 gives a property of graphs with partite representations, formulated by Marquardt [Reference Marquardt15], we include it here for completeness. Lemma 4 is a slight variation of a result of Conlon [Reference Conlon10], about an embedding of a graph in a layer in two different ways. Finally, Lemma 5 is the main lemma needed for Theorem 1. If a graph
![]() $H$
has a
$H$
has a
![]() $k$
-partite representation with representing graph
$k$
-partite representation with representing graph
![]() $H^{\prime}$
, then the vertices of
$H^{\prime}$
, then the vertices of
![]() $H$
corresponding to
$H$
corresponding to
![]() $V(H^{\prime})\cap V_k$
are called top vertices with respect to this representation, and all other vertices are called bottom vertices. Note that if a graph has a
$V(H^{\prime})\cap V_k$
are called top vertices with respect to this representation, and all other vertices are called bottom vertices. Note that if a graph has a
![]() $k$
-partite representation, it has a
$k$
-partite representation, it has a
![]() $(k+1)$
-partite representation that could be seen by simply adding a new element to every vertex of a representing graph.
$(k+1)$
-partite representation that could be seen by simply adding a new element to every vertex of a representing graph.
Lemma 3.
Let
![]() $H$
and
$H$
and
![]() $G$
be connected graphs, each having a
$G$
be connected graphs, each having a
![]() $k$
-partite representation. Assume that
$k$
-partite representation. Assume that
![]() $V(H)\cap V(G)=\{v\}$
, where
$V(H)\cap V(G)=\{v\}$
, where
![]() $v$
is a top vertex for both
$v$
is a top vertex for both
![]() $H$
and
$H$
and
![]() $G$
or a bottom vertex for both
$G$
or a bottom vertex for both
![]() $H$
and
$H$
and
![]() $G$
. Then
$G$
. Then
![]() $H\cup G$
has a partite representation.
$H\cup G$
has a partite representation.
Proof. Let
![]() $H^{\prime}$
and
$H^{\prime}$
and
![]() $G^{\prime}$
be copies of
$G^{\prime}$
be copies of
![]() $H$
and
$H$
and
![]() $G$
that are subgraphs of the
$G$
that are subgraphs of the
![]() $k$
th edge layers in hypercubes with ground sets
$k$
th edge layers in hypercubes with ground sets
![]() $X$
and
$X$
and
![]() $Y$
, respectively, such that
$Y$
, respectively, such that
![]() $V(H^{\prime}) \cap \binom{X}{k}$
and
$V(H^{\prime}) \cap \binom{X}{k}$
and
![]() $V(H^{\prime}) \cap \binom{Y}{k}$
are the edge sets of
$V(H^{\prime}) \cap \binom{Y}{k}$
are the edge sets of
![]() $k$
-partite hypergraphs with parts
$k$
-partite hypergraphs with parts
![]() $U_1,\ldots,U_k$
and parts
$U_1,\ldots,U_k$
and parts
![]() $W_1,\ldots, W_k$
, respectively. Let
$W_1,\ldots, W_k$
, respectively. Let
![]() $u$
and
$u$
and
![]() $w$
be respective copies of
$w$
be respective copies of
![]() $v$
in
$v$
in
![]() $H^{\prime}$
and
$H^{\prime}$
and
![]() $G^{\prime}$
. We shall specify
$G^{\prime}$
. We shall specify
![]() $X$
and
$X$
and
![]() $Y$
in two cases below.
$Y$
in two cases below.
Assume first that
![]() $v$
is a top vertex of
$v$
is a top vertex of
![]() $H$
and of
$H$
and of
![]() $G$
. Let
$G$
. Let
![]() $X$
and
$X$
and
![]() $Y$
be chosen such that
$Y$
be chosen such that
![]() $X\cap Y=\emptyset$
. Let
$X\cap Y=\emptyset$
. Let
![]() $F$
be an induced subgraph of a hypercube
$F$
be an induced subgraph of a hypercube
![]() $Q$
with ground set
$Q$
with ground set
![]() $X\cup Y$
and vertex set
$X\cup Y$
and vertex set
![]() $\{x\cup w\,:\, x\in V(H^{\prime})\}\cup \{u\cup y\,:\, y\in V(G^{\prime})\}$
. We see that
$\{x\cup w\,:\, x\in V(H^{\prime})\}\cup \{u\cup y\,:\, y\in V(G^{\prime})\}$
. We see that
![]() $F$
contains a copy
$F$
contains a copy
![]() $F^{\prime}$
of
$F^{\prime}$
of
![]() $H\cup G$
and is contained in the edge layer
$H\cup G$
and is contained in the edge layer
![]() $2k$
of
$2k$
of
![]() $Q$
with the vertex
$Q$
with the vertex
![]() $u\cup w$
playing a role of
$u\cup w$
playing a role of
![]() $v$
. Moreover,
$v$
. Moreover,
![]() $V(F^{\prime})\cap \binom{X\cup Y}{2k}$
is an edge set of a
$V(F^{\prime})\cap \binom{X\cup Y}{2k}$
is an edge set of a
![]() $2k$
-partite hypergraph with parts
$2k$
-partite hypergraph with parts
![]() $U_1,\ldots,U_k, W_1,\ldots, W_k$
.
$U_1,\ldots,U_k, W_1,\ldots, W_k$
.
Assume now that
![]() $v$
is a bottom vertex of
$v$
is a bottom vertex of
![]() $H$
and of
$H$
and of
![]() $G$
. Let
$G$
. Let
![]() $X$
and
$X$
and
![]() $Y$
be chosen such that
$Y$
be chosen such that
![]() $X\cap Y=[k-1]$
and
$X\cap Y=[k-1]$
and
![]() $u=w=[k-1]$
. Assume further that
$u=w=[k-1]$
. Assume further that
![]() $i\in U_i$
,
$i\in U_i$
,
![]() $i\in W_i$
, for each
$i\in W_i$
, for each
![]() $i\in [k-1]$
. Let
$i\in [k-1]$
. Let
![]() $F$
be an induced subgraph of a hypercube
$F$
be an induced subgraph of a hypercube
![]() $Q$
with ground set
$Q$
with ground set
![]() $X\cup Y$
and vertex set
$X\cup Y$
and vertex set
![]() $V(H^{\prime}) \cup V(G^{\prime})$
. We see that
$V(H^{\prime}) \cup V(G^{\prime})$
. We see that
![]() $F$
contains a copy
$F$
contains a copy
![]() $F^{\prime}$
of
$F^{\prime}$
of
![]() $H\cup G$
and is contained in the edge layer
$H\cup G$
and is contained in the edge layer
![]() $k$
of
$k$
of
![]() $Q$
with vertex
$Q$
with vertex
![]() $v^{\prime}=[k-1]$
playing a role of
$v^{\prime}=[k-1]$
playing a role of
![]() $v$
. Moreover,
$v$
. Moreover,
![]() $V(F^{\prime})\cap \binom{X\cup Y}{k}$
is an edge set of a
$V(F^{\prime})\cap \binom{X\cup Y}{k}$
is an edge set of a
![]() $k$
-partite hypergraph with parts
$k$
-partite hypergraph with parts
![]() $U_1\cup W_1,\ldots,U_k\cup W_k$
.
$U_1\cup W_1,\ldots,U_k\cup W_k$
.
Lemma 4.
Let
![]() $Z$
be a connected bipartite graph with a partite representation. Fix one of the two partite set of
$Z$
be a connected bipartite graph with a partite representation. Fix one of the two partite set of
![]() $Z$
arbitrarily and call its vertices odd. Then for any
$Z$
arbitrarily and call its vertices odd. Then for any
![]() $\gamma \gt 0$
there is
$\gamma \gt 0$
there is
![]() $n_1=n_1(\gamma,Z)$
such that for any
$n_1=n_1(\gamma,Z)$
such that for any
![]() $n\gt n_1$
the following holds. Let
$n\gt n_1$
the following holds. Let
![]() $L_j$
be the
$L_j$
be the
![]() $j$
th edge layer of
$j$
th edge layer of
![]() $Q_n$
, where
$Q_n$
, where
![]() $n/2 -n^{2/3} \leq j\leq n/2 + n^{2/3}$
. Let
$n/2 -n^{2/3} \leq j\leq n/2 + n^{2/3}$
. Let
![]() $G\subseteq L_j$
be a graph such that
$G\subseteq L_j$
be a graph such that
![]() $||G||\geq \gamma ||L_j||$
. Then there is a copy of
$||G||\geq \gamma ||L_j||$
. Then there is a copy of
![]() $Z$
with odd vertices in
$Z$
with odd vertices in
![]() $V_j$
and there is a copy of
$V_j$
and there is a copy of
![]() $Z$
in
$Z$
in
![]() $G$
with odd vertices in
$G$
with odd vertices in
![]() $V_{j-1}$
.
$V_{j-1}$
.
Proof. Let
![]() $Z$
have a
$Z$
have a
![]() $k$
-partite representation in a hypercube
$k$
-partite representation in a hypercube
![]() $Q_n$
with ground set
$Q_n$
with ground set
![]() $[n]$
. We need the following notation. For any
$[n]$
. We need the following notation. For any
![]() $x\in V(Q_n)$
, let
$x\in V(Q_n)$
, let
![]() $\textrm{Up}(x)$
be the up set of
$\textrm{Up}(x)$
be the up set of
![]() $x$
, that is,
$x$
, that is,
![]() $\textrm{Up}(x) = \{ y \subseteq [n]\,:$
$\textrm{Up}(x) = \{ y \subseteq [n]\,:$
![]() $x\subseteq y\}$
. Note that
$x\subseteq y\}$
. Note that
![]() $\textrm{Up}(x)$
induces a graph isomorphic to
$\textrm{Up}(x)$
induces a graph isomorphic to
![]() $Q_m$
, for
$Q_m$
, for
![]() $m= n-|x|$
.
$m= n-|x|$
.
We need to consider four cases according to whether the odd vertices of
![]() $Z$
correspond to
$Z$
correspond to
![]() $k$
- or
$k$
- or
![]() $(k-1)$
-element sets in the representation and whether we are embedding the odd vertices in
$(k-1)$
-element sets in the representation and whether we are embedding the odd vertices in
![]() $V_j$
or in
$V_j$
or in
![]() $V_{j-1}$
. Note, however, that we can assume that the odd vertices correspond to the
$V_{j-1}$
. Note, however, that we can assume that the odd vertices correspond to the
![]() $k$
-element sets of the representation by selecting the vertices of other partite set of
$k$
-element sets of the representation by selecting the vertices of other partite set of
![]() $Z$
as odd vertices instead.
$Z$
as odd vertices instead.
So, from now on, we assume first that the odd vertices of
![]() $Z$
correspond to the
$Z$
correspond to the
![]() $k$
-element sets of the representation.
$k$
-element sets of the representation.
We shall first a copy of
![]() $Z$
in
$Z$
in
![]() $G$
with odd vertices in
$G$
with odd vertices in
![]() $V_{j}$
.
$V_{j}$
.
Let
![]() $U_x= U_{x,k}$
be the intersection of
$U_x= U_{x,k}$
be the intersection of
![]() $G$
and the
$G$
and the
![]() $k$
th edge layer of the hypercube
$k$
th edge layer of the hypercube
![]() $Q$
induced by
$Q$
induced by
![]() $\textrm{Up}(x)$
, for each
$\textrm{Up}(x)$
, for each
![]() $x\in V_{j-k}$
. Note that
$x\in V_{j-k}$
. Note that
![]() $U_x$
is a subgraph of
$U_x$
is a subgraph of
![]() $L_j$
, the
$L_j$
, the
![]() $j$
th layer of
$j$
th layer of
![]() $Q_n$
. We call a vertex
$Q_n$
. We call a vertex
![]() $y$
of
$y$
of
![]() $U_x$
a full vertex if it has degree
$U_x$
a full vertex if it has degree
![]() $k$
in
$k$
in
![]() $U_x$
, the largest possible degree. Let
$U_x$
, the largest possible degree. Let
![]() $u_x$
be the number of full vertices in
$u_x$
be the number of full vertices in
![]() $U_x$
. We shall argue that there is a vertex
$U_x$
. We shall argue that there is a vertex
![]() $x \in V_{j-k}$
such that
$x \in V_{j-k}$
such that
![]() $u_x$
is large.
$u_x$
is large.
Let
![]() $t$
be the number of
$t$
be the number of
![]() $k$
-edge stars in
$k$
-edge stars in
![]() $G$
with the centre in
$G$
with the centre in
![]() $V_{j}$
. Then
$V_{j}$
. Then
 \begin{equation*}t = \sum _{y\in V_{j}} \binom {d_G(y)}{k} \geq |V_{j}| \binom {\gamma ||L_j||/|V_{j}|}{k}.\end{equation*}
\begin{equation*}t = \sum _{y\in V_{j}} \binom {d_G(y)}{k} \geq |V_{j}| \binom {\gamma ||L_j||/|V_{j}|}{k}.\end{equation*}
Each such a star corresponds to a full vertex in
![]() $U_x$
, for some
$U_x$
, for some
![]() $x$
. Thus,
$x$
. Thus,
![]() $\sum _{x\in V_{j-k}} u_x \geq t$
and there is a vertex
$\sum _{x\in V_{j-k}} u_x \geq t$
and there is a vertex
![]() $x$
such that
$x$
such that
Since
![]() $n/2 -n^{2/3} \leq j\leq n/2 + n^{2/3}$
and
$n/2 -n^{2/3} \leq j\leq n/2 + n^{2/3}$
and
![]() $k$
is a fixed constant, we have that
$k$
is a fixed constant, we have that
![]() $||L_j||/|V_j| = \frac{n}{2}(1+o(1))$
and
$||L_j||/|V_j| = \frac{n}{2}(1+o(1))$
and
![]() $|V_j|/|V_{j-k}| \geq c^{\prime}(k)$
, so
$|V_j|/|V_{j-k}| \geq c^{\prime}(k)$
, so
for positive constants
![]() $c(k)$
and
$c(k)$
and
![]() $c^{\prime}(k)$
. Consider the full vertices in
$c^{\prime}(k)$
. Consider the full vertices in
![]() $U_x$
. They correspond to
$U_x$
. They correspond to
![]() $u_x$
hyperedges in a
$u_x$
hyperedges in a
![]() $k$
-uniform hypergraph with the vertex set
$k$
-uniform hypergraph with the vertex set
![]() $[n]-x$
of size
$[n]-x$
of size
![]() $n-j+k = \frac{n}{2} (1+o(1))$
. By a theorem of Erdős [Reference Erdős11], such a hypergraph contains any fixed
$n-j+k = \frac{n}{2} (1+o(1))$
. By a theorem of Erdős [Reference Erdős11], such a hypergraph contains any fixed
![]() $k$
-partite
$k$
-partite
![]() $k$
-uniform hypergraph, and thus in particular the one representing
$k$
-uniform hypergraph, and thus in particular the one representing
![]() $Z$
. Therefore,
$Z$
. Therefore,
![]() $G$
contains a copy of
$G$
contains a copy of
![]() $Z$
with odd vertices in
$Z$
with odd vertices in
![]() $V_j$
.
$V_j$
.
Next, we shall find a copy of
![]() $Z$
in
$Z$
in
![]() $G$
with odd vertices in
$G$
with odd vertices in
![]() $V_{j-1}$
. To do this, we repeat the above argument by considering the vertices
$V_{j-1}$
. To do this, we repeat the above argument by considering the vertices
![]() $x$
in
$x$
in
![]() $V_{j+k-1}$
and their downsets. Alternatively, we see that
$V_{j+k-1}$
and their downsets. Alternatively, we see that
![]() $L_j$
corresponds to
$L_j$
corresponds to
![]() $L_{j^{\prime}}$
, a “symmetric” layer, where
$L_{j^{\prime}}$
, a “symmetric” layer, where
![]() $j^{\prime}=n+1-j$
,
$j^{\prime}=n+1-j$
,
![]() $V_{j^{\prime}}$
corresponds to
$V_{j^{\prime}}$
corresponds to
![]() $V_{j-1}$
, and
$V_{j-1}$
, and
![]() $V_{j^{\prime}-1}$
corresponds to
$V_{j^{\prime}-1}$
corresponds to
![]() $V_j$
. Thus, finding a copy of
$V_j$
. Thus, finding a copy of
![]() $Z$
in
$Z$
in
![]() $L_{j^{\prime}}$
with odd vertices in
$L_{j^{\prime}}$
with odd vertices in
![]() $V_{j^{\prime}}$
corresponds to finding a copy of
$V_{j^{\prime}}$
corresponds to finding a copy of
![]() $Z$
in
$Z$
in
![]() $L_j$
with odd vertices in
$L_j$
with odd vertices in
![]() $V_{j-1}$
. Since
$V_{j-1}$
. Since
![]() $j^{\prime}$
satisfies the same conditions as
$j^{\prime}$
satisfies the same conditions as
![]() $j$
, that is,
$j$
, that is,
![]() $n/2 -n^{2/3} \leq j^{\prime} \leq n/2 + n^{2/3}$
, we thus could use the first part of the Lemma to obtain the second one.
$n/2 -n^{2/3} \leq j^{\prime} \leq n/2 + n^{2/3}$
, we thus could use the first part of the Lemma to obtain the second one.
Lemma 5.
Let
![]() $H$
be a connected bipartite graph with
$H$
be a connected bipartite graph with
![]() $\ell$
blocks, where every block has a partite representation. Then for any
$\ell$
blocks, where every block has a partite representation. Then for any
![]() $\gamma \gt 0$
there is
$\gamma \gt 0$
there is
![]() $n_0=n_0(\gamma, H)$
such that for any
$n_0=n_0(\gamma, H)$
such that for any
![]() $n\gt n_0$
the following holds. Let
$n\gt n_0$
the following holds. Let
![]() $L_j$
be the
$L_j$
be the
![]() $j$
th edge layer of
$j$
th edge layer of
![]() $Q_n$
, where
$Q_n$
, where
![]() $n/2 -n^{2/3} \leq j\leq n/2 + n^{2/3}$
. Let
$n/2 -n^{2/3} \leq j\leq n/2 + n^{2/3}$
. Let
![]() $G\subseteq L_j$
be a graph with
$G\subseteq L_j$
be a graph with
![]() $||G||= \gamma ||L_j||$
. Fix one of two partite sets of
$||G||= \gamma ||L_j||$
. Fix one of two partite sets of
![]() $H$
arbitrarily and call its vertices odd. Then there is a copy of
$H$
arbitrarily and call its vertices odd. Then there is a copy of
![]() $H$
in
$H$
in
![]() $G$
with odd vertices in
$G$
with odd vertices in
![]() $V_j$
and there is a copy of
$V_j$
and there is a copy of
![]() $H$
in
$H$
in
![]() $G$
with odd vertices in
$G$
with odd vertices in
![]() $V_{j-1}$
.
$V_{j-1}$
.
Proof. We shall prove the statement by induction on
![]() $\ell$
with the base case
$\ell$
with the base case
![]() $\ell =1$
directly following from Lemma 4.
$\ell =1$
directly following from Lemma 4.
If
![]() $H$
has
$H$
has
![]() $\ell$
blocks,
$\ell$
blocks,
![]() $\ell \geq 2$
, such that each has a
$\ell \geq 2$
, such that each has a
![]() $k$
-partite representation, let
$k$
-partite representation, let
![]() $H=H^{\prime}\cup H^{\prime\prime}$
, where
$H=H^{\prime}\cup H^{\prime\prime}$
, where
![]() $H^{\prime}$
and
$H^{\prime}$
and
![]() $H^{\prime\prime}$
share a single vertex
$H^{\prime\prime}$
share a single vertex
![]() $v^{\prime}$
, and
$v^{\prime}$
, and
![]() $H^{\prime\prime}$
is a block of
$H^{\prime\prime}$
is a block of
![]() $H$
, that is, a leaf block. Let
$H$
, that is, a leaf block. Let
![]() $F$
be a graph that is a union of
$F$
be a graph that is a union of
![]() $q\gt |V(H^{\prime})|$
copies
$q\gt |V(H^{\prime})|$
copies
![]() $F_1, \ldots, F_q$
of
$F_1, \ldots, F_q$
of
![]() $H^{\prime\prime}$
that pairwise share only a vertex corresponding to
$H^{\prime\prime}$
that pairwise share only a vertex corresponding to
![]() $v^{\prime}$
. Let
$v^{\prime}$
. Let
![]() $\gamma \gt 0$
and
$\gamma \gt 0$
and
![]() $n_0$
be sufficiently large (we shall specify how large later). Let
$n_0$
be sufficiently large (we shall specify how large later). Let
![]() $G\subseteq L_j$
,
$G\subseteq L_j$
,
![]() $||G||=\gamma ||L_j||$
.
$||G||=\gamma ||L_j||$
.
Assume first that
![]() $v^{\prime}$
is an odd vertex.
$v^{\prime}$
is an odd vertex.
The idea of the proof is as follows. We shall first find many copies of
![]() $H^{\prime}$
in
$H^{\prime}$
in
![]() $G$
for which the vertex corresponding to
$G$
for which the vertex corresponding to
![]() $v^{\prime}$
is in
$v^{\prime}$
is in
![]() $V_j$
. Then we shall find a copy
$V_j$
. Then we shall find a copy
![]() $F^*$
of
$F^*$
of
![]() $F$
and a copy
$F$
and a copy
![]() $H^*$
of
$H^*$
of
![]() $H^{\prime}$
such that
$H^{\prime}$
such that
![]() $V(F^*)\cap V(H^*) \cap V_j = \{v\}$
, where
$V(F^*)\cap V(H^*) \cap V_j = \{v\}$
, where
![]() $v$
plays a role of
$v$
plays a role of
![]() $v^{\prime}$
. Finally, since
$v^{\prime}$
. Finally, since
![]() $q$
is large enough, we shall claim that there is a copy
$q$
is large enough, we shall claim that there is a copy
![]() $F_i^*$
of
$F_i^*$
of
![]() $F_i$
for some
$F_i$
for some
![]() $i$
such that
$i$
such that
![]() $V(F_i^*)\cap V(H^*) \cap V_{j-1} = \emptyset$
. This will imply that
$V(F_i^*)\cap V(H^*) \cap V_{j-1} = \emptyset$
. This will imply that
![]() $F^*_i \cup H^*$
is a copy of
$F^*_i \cup H^*$
is a copy of
![]() $H$
. Next, we shall give the details of this argument:
$H$
. Next, we shall give the details of this argument:
First, we shall construct sets
![]() $V^{(1)}, V^{(2)},$
and
$V^{(1)}, V^{(2)},$
and
![]() $V^{(3)}$
, such that
$V^{(3)}$
, such that
![]() $V^{(3)}\subseteq V^{(2)} \subseteq V^{(1)}\subseteq V_j$
as follows:
$V^{(3)}\subseteq V^{(2)} \subseteq V^{(1)}\subseteq V_j$
as follows:
Assume that
![]() $n_0\gt n_0(\gamma/4, H^{\prime})$
. Consider all copies of
$n_0\gt n_0(\gamma/4, H^{\prime})$
. Consider all copies of
![]() $H^{\prime}$
in
$H^{\prime}$
in
![]() $G$
with a vertex playing a role of
$G$
with a vertex playing a role of
![]() $v^{\prime}$
in
$v^{\prime}$
in
![]() $V_j$
. Let
$V_j$
. Let
![]() $V^{(1)}\subseteq V_j$
be the set of all such vertices playing a role of
$V^{(1)}\subseteq V_j$
be the set of all such vertices playing a role of
![]() $v^{\prime}$
in some copy of
$v^{\prime}$
in some copy of
![]() $H^{\prime}$
in
$H^{\prime}$
in
![]() $G$
. Note that
$G$
. Note that
![]() $\big|\big|G\big[\big(V_j-V^{(1)}\big) \cup V_{j-1}\big]\big|\big| \lt \frac{1}{4} \gamma ||L_j||$
, otherwise by induction we can find another copy of
$\big|\big|G\big[\big(V_j-V^{(1)}\big) \cup V_{j-1}\big]\big|\big| \lt \frac{1}{4} \gamma ||L_j||$
, otherwise by induction we can find another copy of
![]() $H^{\prime}$
with a vertex
$H^{\prime}$
with a vertex
![]() $w\in V_j-V^{(1)}$
playing a role of
$w\in V_j-V^{(1)}$
playing a role of
![]() $v^{\prime}$
, contradicting the definition of
$v^{\prime}$
, contradicting the definition of
![]() $V^{(1)}$
. Note, that for each
$V^{(1)}$
. Note, that for each
![]() $v\in V^{(1)}$
, there could be several copies of
$v\in V^{(1)}$
, there could be several copies of
![]() $H^{\prime}$
with
$H^{\prime}$
with
![]() $v$
playing a role of
$v$
playing a role of
![]() $v^{\prime}$
. We choose one such copy arbitrarily and denote it
$v^{\prime}$
. We choose one such copy arbitrarily and denote it
![]() $H^{\prime}_v$
. Let
$H^{\prime}_v$
. Let
The total number of edges of
![]() $G$
not incident to
$G$
not incident to
![]() $V^{(2)}$
is at most
$V^{(2)}$
is at most
![]() $\frac{1}{4}\gamma ||L_j||+ \frac{1}{2}||G||= \frac{3}{4}\gamma ||L_j||$
. Thus,
$\frac{1}{4}\gamma ||L_j||+ \frac{1}{2}||G||= \frac{3}{4}\gamma ||L_j||$
. Thus,
![]() $\big|\big|G\big[V^{(2)} \cup V_{j-1}\big]\big|\big| \geq \frac{\gamma }{4}||L_j||$
. Since all vertices from
$\big|\big|G\big[V^{(2)} \cup V_{j-1}\big]\big|\big| \geq \frac{\gamma }{4}||L_j||$
. Since all vertices from
![]() $V_j$
in
$V_j$
in
![]() $L_j$
have the same degree,
$L_j$
have the same degree,
Let for each
![]() $v\in V^{(2)}$
,
$v\in V^{(2)}$
,
![]() $A_v\subseteq V_j$
and
$A_v\subseteq V_j$
and
![]() $B_v\subseteq V_{j-1}$
be sets of vertices such that
$B_v\subseteq V_{j-1}$
be sets of vertices such that
![]() $V(H^{\prime}_v)=A_v\cup B_v\cup \{v\}$
,
$V(H^{\prime}_v)=A_v\cup B_v\cup \{v\}$
,
![]() $v\not \in A_v$
. Randomly colour each vertex in
$v\not \in A_v$
. Randomly colour each vertex in
![]() $V^{(2)}$
with red or blue independently with equal probability and colour the vertices in
$V^{(2)}$
with red or blue independently with equal probability and colour the vertices in
![]() $V_j-V^{(2)}$
blue. We say that a vertex
$V_j-V^{(2)}$
blue. We say that a vertex
![]() $v\in V^{(2)}$
is good if
$v\in V^{(2)}$
is good if
![]() $v$
is red and each vertex in
$v$
is red and each vertex in
![]() $A_v$
is blue. Then, the expected number of good
$A_v$
is blue. Then, the expected number of good
![]() $v$
’s is at least
$v$
’s is at least
![]() $|V^{(2)}|2^{-t}$
, where
$|V^{(2)}|2^{-t}$
, where
![]() $|A_v|=t-1$
. Thus, there is a set
$|A_v|=t-1$
. Thus, there is a set
![]() $V^{(3)}\subseteq V^{(2)}$
, corresponding to a set of good
$V^{(3)}\subseteq V^{(2)}$
, corresponding to a set of good
![]() $v$
’s, with
$v$
’s, with
![]() $|V^{(3)}|\geq |V^{(2)}|2^{-t}$
, such that for each
$|V^{(3)}|\geq |V^{(2)}|2^{-t}$
, such that for each
![]() $v\in V^{(3)}$
,
$v\in V^{(3)}$
,
![]() $A_v \cap V^{(3)} = \emptyset$
.
$A_v \cap V^{(3)} = \emptyset$
.
We see that
Consider the graph
![]() $F$
defined above. By Lemma 3,
$F$
defined above. By Lemma 3,
![]() $F$
has a partite representation. Then by Lemma 4, there is a copy
$F$
has a partite representation. Then by Lemma 4, there is a copy
![]() $F^*$
of
$F^*$
of
![]() $F$
in
$F$
in
![]() $G\big[V^{(3)}\cup V_{j-1}\big]$
with a vertex
$G\big[V^{(3)}\cup V_{j-1}\big]$
with a vertex
![]() $v\in V^{(3)}$
corresponding to
$v\in V^{(3)}$
corresponding to
![]() $v^{\prime}$
. Here, we assume that
$v^{\prime}$
. Here, we assume that
![]() $n_0\gt n_1\big(\gamma ^2 2^{-t-3}, F\big)$
. Let
$n_0\gt n_1\big(\gamma ^2 2^{-t-3}, F\big)$
. Let
![]() $F_i^*$
be a respective copy of
$F_i^*$
be a respective copy of
![]() $F_i$
, for each
$F_i$
, for each
![]() $i\in [q]$
. By construction of
$i\in [q]$
. By construction of
![]() $V^{(3)}$
, there is a copy
$V^{(3)}$
, there is a copy
![]() $H^*$
of
$H^*$
of
![]() $H^{\prime}$
in
$H^{\prime}$
in
![]() $G$
with all vertices except for
$G$
with all vertices except for
![]() $v$
not in
$v$
not in
![]() $V^{(3)}$
. Let
$V^{(3)}$
. Let
![]() $B_v$
be the set of vertices of
$B_v$
be the set of vertices of
![]() $H^*$
in
$H^*$
in
![]() $V_{j-1}$
. We see that
$V_{j-1}$
. We see that
![]() $V(F^*) \cap V(H^*) \cap V_j = \{v\}$
. Since
$V(F^*) \cap V(H^*) \cap V_j = \{v\}$
. Since
![]() $q\gt |V(H^{\prime})|\gt |B_v|$
, there is
$q\gt |V(H^{\prime})|\gt |B_v|$
, there is
![]() $i \in [q]$
, such that
$i \in [q]$
, such that
![]() $V(F^*_i)\cap B_v\cap V_{j-1} = \emptyset$
. Then
$V(F^*_i)\cap B_v\cap V_{j-1} = \emptyset$
. Then
![]() $H^*\cup F_i^*$
is a copy of
$H^*\cup F_i^*$
is a copy of
![]() $H$
in
$H$
in
![]() $G$
.
$G$
.
The case when
![]() $v^{\prime}$
is not an odd vertex is treated similarly by first finding many copies of
$v^{\prime}$
is not an odd vertex is treated similarly by first finding many copies of
![]() $H^{\prime}$
with a vertex corresponding to
$H^{\prime}$
with a vertex corresponding to
![]() $v^{\prime}$
in
$v^{\prime}$
in
![]() $V_{j-1}$
.
$V_{j-1}$
.
Proof of Theorem 1. Let
![]() $G^{\prime}$
be a subgraph of
$G^{\prime}$
be a subgraph of
![]() $Q_n$
such that
$Q_n$
such that
![]() $||G^{\prime}|| = 2\gamma ||Q_n||$
, for some constant
$||G^{\prime}|| = 2\gamma ||Q_n||$
, for some constant
![]() $\gamma \gt 0$
and sufficiently large
$\gamma \gt 0$
and sufficiently large
![]() $n$
. By a standard argument, see for example Lemma 1 [Reference Axenovich, Manske and Martin4],
$n$
. By a standard argument, see for example Lemma 1 [Reference Axenovich, Manske and Martin4],
 \begin{equation*}\sum _{i:|i-n/2|\gt n^{2/3}} \binom {n}{i} = o(2^n).\end{equation*}
\begin{equation*}\sum _{i:|i-n/2|\gt n^{2/3}} \binom {n}{i} = o(2^n).\end{equation*}
Since the degree of each vertex in
![]() $Q_n$
is
$Q_n$
is
![]() $n$
, the total number of edges in
$n$
, the total number of edges in
![]() $G^{\prime}$
, incident to vertices in
$G^{\prime}$
, incident to vertices in
![]() $V_i$
’s, for
$V_i$
’s, for
![]() $i\lt n/2 - n^{2/3}$
or
$i\lt n/2 - n^{2/3}$
or
![]() $ i \gt n/2 +n^{2/3}$
is
$ i \gt n/2 +n^{2/3}$
is
![]() $o(n2^n) = o(||Q_n||) = o(||G||)$
. Then there is
$o(n2^n) = o(||Q_n||) = o(||G||)$
. Then there is
![]() $j\in \big\{n/2 - n^{2/3}, n/2 + n^{2/3}\big\}$
such that
$j\in \big\{n/2 - n^{2/3}, n/2 + n^{2/3}\big\}$
such that
![]() $L_j$
contains at least
$L_j$
contains at least
![]() $\gamma ||L_i||$
edges of
$\gamma ||L_i||$
edges of
![]() $G^{\prime}$
. Lemma 5 applied to
$G^{\prime}$
. Lemma 5 applied to
![]() $G= G^{\prime}\cap L_j$
concludes the proof.
$G= G^{\prime}\cap L_j$
concludes the proof.
Proof of Theorem
2. Let
![]() $H=H(q)$
be a union of two copies
$H=H(q)$
be a union of two copies
![]() $\Theta _1$
and
$\Theta _1$
and
![]() $\Theta _2$
of
$\Theta _2$
of
![]() $\Theta (q)$
sharing exactly one vertex that is a main pole of
$\Theta (q)$
sharing exactly one vertex that is a main pole of
![]() $\Theta _2$
and a subdivision vertex of
$\Theta _2$
and a subdivision vertex of
![]() $\Theta _1$
.
$\Theta _1$
.
First, we need to check that
![]() $H(q)$
is cubical. Marquardt [Reference Marquardt15] gave an explicit embedding of
$H(q)$
is cubical. Marquardt [Reference Marquardt15] gave an explicit embedding of
![]() $H(3)$
in a hypercube. We show that
$H(3)$
in a hypercube. We show that
![]() $H(q)$
is cubical by constructing its nice colouring by taking nice colourings of
$H(q)$
is cubical by constructing its nice colouring by taking nice colourings of
![]() $\Theta _1$
and
$\Theta _1$
and
![]() $\Theta _2$
using disjoint sets of colours. These colourings were given in [Reference Havel and Morávek14] and we show one in Fig. 1.
$\Theta _2$
using disjoint sets of colours. These colourings were given in [Reference Havel and Morávek14] and we show one in Fig. 1.
Next, we shall show that
![]() $H(q)$
has no partite representation. The Hamming distance between two binary vectors
$H(q)$
has no partite representation. The Hamming distance between two binary vectors
![]() $u$
and
$u$
and
![]() $v$
, denoted
$v$
, denoted
![]() $d_H(u,v)$
is the number of positions where the vectors differ. In [Reference Axenovich, Martin and Winter2], it is shown that if
$d_H(u,v)$
is the number of positions where the vectors differ. In [Reference Axenovich, Martin and Winter2], it is shown that if
![]() $q\geq 3$
and
$q\geq 3$
and
![]() $v, v^{\prime}$
are the main poles of a copy of
$v, v^{\prime}$
are the main poles of a copy of
![]() $\Theta (q)$
embedded in a layer of a hypercube, then
$\Theta (q)$
embedded in a layer of a hypercube, then
![]() $d_H(v, v^{\prime})=2$
. Let the main poles of
$d_H(v, v^{\prime})=2$
. Let the main poles of
![]() $\Theta _1$
and
$\Theta _1$
and
![]() $\Theta _2$
be denoted
$\Theta _2$
be denoted
![]() $v_i, v^{\prime}_i$
, respectively,
$v_i, v^{\prime}_i$
, respectively,
![]() $i=1,2$
. Assume that
$i=1,2$
. Assume that
![]() $H$
has a
$H$
has a
![]() $k$
-partite representation for some
$k$
-partite representation for some
![]() $k$
, that is,
$k$
, that is,
![]() $V(H)\subseteq \binom{[n]}{k}\cup \binom{[n]}{k-1}$
, for some
$V(H)\subseteq \binom{[n]}{k}\cup \binom{[n]}{k-1}$
, for some
![]() $n$
and
$n$
and
![]() $V(H)\cap \binom{[n]}{k}$
corresponds to the edges of a
$V(H)\cap \binom{[n]}{k}$
corresponds to the edges of a
![]() $k$
-partite hypergraph, denote it by
$k$
-partite hypergraph, denote it by
![]() $\mathcal{H}$
. We have that
$\mathcal{H}$
. We have that
![]() $d_H(v_i, v^{\prime}_i)=2$
,
$d_H(v_i, v^{\prime}_i)=2$
,
![]() $i=1,2$
. Since a main pole of
$i=1,2$
. Since a main pole of
![]() $\Theta _1$
and a main pole of
$\Theta _1$
and a main pole of
![]() $\Theta _2$
are adjacent, the main poles of
$\Theta _2$
are adjacent, the main poles of
![]() $\Theta _1$
are in one vertex layer and the main poles of
$\Theta _1$
are in one vertex layer and the main poles of
![]() $\Theta _2$
are in another vertex layer, without loss of generality,
$\Theta _2$
are in another vertex layer, without loss of generality,
![]() $v_1, v^{\prime}_1 \in \binom{[n]}{k}$
and
$v_1, v^{\prime}_1 \in \binom{[n]}{k}$
and
![]() $v_2, v^{\prime}_2 \in \binom{[n]}{k-1}$
. Assume further that
$v_2, v^{\prime}_2 \in \binom{[n]}{k-1}$
. Assume further that
![]() $v_1$
and
$v_1$
and
![]() $v^{\prime}_1$
equal to
$v^{\prime}_1$
equal to
![]() $10$
and
$10$
and
![]() $01$
in the first two positions of their binary representation and coincide on all other positions. Consider neighbours of
$01$
in the first two positions of their binary representation and coincide on all other positions. Consider neighbours of
![]() $v_1$
in
$v_1$
in
![]() $\Theta _1$
. At least one of these neighbours, say
$\Theta _1$
. At least one of these neighbours, say
![]() $w$
differs from
$w$
differs from
![]() $v_1$
in a position that is not one of the first two ones, say in the third position. Then, restricted to the first three position
$v_1$
in a position that is not one of the first two ones, say in the third position. Then, restricted to the first three position
![]() $v_1$
is
$v_1$
is
![]() $101$
,
$101$
,
![]() $w$
is
$w$
is
![]() $100$
, and
$100$
, and
![]() $v^{\prime}_1$
is
$v^{\prime}_1$
is
![]() $011$
. Thus, the remaining two vertices on the
$011$
. Thus, the remaining two vertices on the
![]() $v_1, v^{\prime}_1$
path, that contains
$v_1, v^{\prime}_1$
path, that contains
![]() $w$
, must be equal to
$w$
, must be equal to
![]() $110$
and
$110$
and
![]() $010$
in these three position. All vertices of this leg are the same in positions
$010$
in these three position. All vertices of this leg are the same in positions
![]() $4, \ldots, n$
, say they are equal to
$4, \ldots, n$
, say they are equal to
![]() $1$
on a set of positions
$1$
on a set of positions
![]() $A\subseteq \{4, \ldots, n\}$
,
$A\subseteq \{4, \ldots, n\}$
,
![]() $|A|=k-2$
. Thus, we have that
$|A|=k-2$
. Thus, we have that
![]() $\mathcal{H}^{\prime}$
contains hyperedges
$\mathcal{H}^{\prime}$
contains hyperedges
![]() $\{1, 2\}\cup A$
,
$\{1, 2\}\cup A$
,
![]() $\{2,3\} \cup A$
, and
$\{2,3\} \cup A$
, and
![]() $\{1, 3\} \cup A$
. If
$\{1, 3\} \cup A$
. If
![]() $\mathcal{H}$
were to be
$\mathcal{H}$
were to be
![]() $k$
-partite,
$k$
-partite,
![]() $1, 2, 3$
and each element of
$1, 2, 3$
and each element of
![]() $A$
would belong to distinct parts, that is, to
$A$
would belong to distinct parts, that is, to
![]() $k+1$
parts, a contradiction. This shows that
$k+1$
parts, a contradiction. This shows that
![]() $H(q)$
has no partite representation.
$H(q)$
has no partite representation.
Finally, we shall show that
![]() $H(q)$
has zero Turán density in a hypercube. Using Theorem 1 it is sufficient to show that
$H(q)$
has zero Turán density in a hypercube. Using Theorem 1 it is sufficient to show that
![]() $\Theta (q)$
has partite representation. Note that
$\Theta (q)$
has partite representation. Note that
![]() $\Theta (q) = K_{2,q}(1)$
, a subdivision of
$\Theta (q) = K_{2,q}(1)$
, a subdivision of
![]() $K_{2,q}$
. We claim that
$K_{2,q}$
. We claim that
![]() $\mathcal{H} = K_{2,q}$
gives a
$\mathcal{H} = K_{2,q}$
gives a
![]() $2$
-partite representation of
$2$
-partite representation of
![]() $\Theta (q)$
. Indeed, let
$\Theta (q)$
. Indeed, let
![]() $n= q+2$
and let
$n= q+2$
and let
![]() $\mathcal{H}$
be a hypergraph on a vertex set
$\mathcal{H}$
be a hypergraph on a vertex set
![]() $[n]$
with the edge set
$[n]$
with the edge set
![]() $\{ij\,:\, i\in [2], j\in [n]\setminus [2]\}$
. So,
$\{ij\,:\, i\in [2], j\in [n]\setminus [2]\}$
. So,
![]() $\mathcal{H}$
is a bipartite graph, that is,
$\mathcal{H}$
is a bipartite graph, that is,
![]() $2$
-partite
$2$
-partite
![]() $2$
-uniform hypergraph. Let the edges of
$2$
-uniform hypergraph. Let the edges of
![]() $\mathcal{H}$
correspond to subdivision vertices of
$\mathcal{H}$
correspond to subdivision vertices of
![]() $K_{2,q}(1)$
. Let vertices
$K_{2,q}(1)$
. Let vertices
![]() $v$
and
$v$
and
![]() $v^{\prime}$
correspond to the main poles of
$v^{\prime}$
correspond to the main poles of
![]() $\Theta (q)$
and vertices
$\Theta (q)$
and vertices
![]() $1, \ldots, q$
correspond to other vertices. Then, the two parts of
$1, \ldots, q$
correspond to other vertices. Then, the two parts of
![]() $\mathcal{H}$
are
$\mathcal{H}$
are
![]() $\{v,v^{\prime}\}$
and
$\{v,v^{\prime}\}$
and
![]() $\{1, \ldots, q\}$
. This concludes the proof of Theorem 2.
$\{1, \ldots, q\}$
. This concludes the proof of Theorem 2.
Conclusions
We showed that there are cubical graphs that have no partite representation and have zero Turán density in a hypercube. On the other hand, we proved that any graph whose every block has a partite representation has zero Turán density in a hypercube. This leads to a followup question:
Open question
Is it true that each cubical graph that is
![]() $2$
-connected and has zero Turán density in a hypercube has a partite representation?
$2$
-connected and has zero Turán density in a hypercube has a partite representation?
Acknowledgements
The author thanks Christian Winter and the anonymous referee for several very constructive comments on the manuscript. The research was supported in part by a DFG grant FKZ AX 93/2-1.