Many screening tests dichotomize a measurement to classify subjects. Typically a cut-off value is chosen in a way that allows identification of an acceptable number of cases relative to a reference procedure, but does not produce too many false positives at the same time. Thus for the same sample many pairs of sensitivities and false positive rates result as the cut-off is varied. The curve of these points is called the receiver operating characteristic (ROC) curve. One goal of diagnostic meta-analysis is to integrate ROC curves and arrive at a summary ROC (SROC) curve. Holling, Böhning, and Böhning (Psychometrika 77:106–126, 2012a) demonstrated that finite semiparametric mixtures can describe the heterogeneity in a sample of Lehmann ROC curves well; this approach leads to clusters of SROC curves of a particular shape. We extend this work with the help of the $t_{\mathit{\alpha }}$\documentclass[12pt]{minimal}\usepackage{amsmath}\usepackage{wasysym}\usepackage{amsfonts}\usepackage{amssymb}\usepackage{amsbsy}\usepackage{mathrsfs}\usepackage{upgreek}\setlength{\oddsidemargin}{-69pt}\begin{document}$$t_{\alpha }$$\end{document}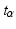 transformation, a flexible family of transformations for proportions. A collection of SROC curves is constructed that approximately contains the Lehmann family but in addition allows the modeling of shapes beyond the Lehmann ROC curves. We introduce two rationales for determining the shape from the data. Using the fact that each curve corresponds to a natural univariate measure of diagnostic accuracy, we show how covariate adjusted mixtures lead to a meta-regression on SROC curves. Three worked examples illustrate the method.