Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Zapf, Antonia
2018.
Diagnostic Meta-Analysis.
p.
125.
Doebler, Philipp
Bürkner, Paul-Christian
and
Rücker, Gerta
2018.
Diagnostic Meta-Analysis.
p.
161.
Bürkner, Paul-Christian
2018.
Diagnostic Meta-Analysis.
p.
115.
Platzek, Ivan
Sieron, Dominik
Plodeck, Verena
Borkowetz, Angelika
Laniado, Michael
and
Hoffmann, Ralf-Thorsten
2019.
Chemical shift imaging for evaluation of adrenal masses: a systematic review and meta-analysis.
European Radiology,
Vol. 29,
Issue. 2,
p.
806.
Holling, Heinz
Böhning, Walailuck
Masoudi, Ehsan
Böhning, Dankmar
and
Sangnawakij, Patarawan
2020.
Evaluation of a new version of I2 with emphasis on diagnostic problems.
Communications in Statistics - Simulation and Computation,
Vol. 49,
Issue. 4,
p.
942.
Yang, Cheng-Hong
Moi, Sin-Hua
Chuang, Li-Yeh
and
Chen, Jin-Bor
2020.
Higher-order clinical risk factor interaction analysis for overall mortality in maintenance hemodialysis patients.
Therapeutic Advances in Chronic Disease,
Vol. 11,
Issue. ,
Hopkins, Danielle
Rickwood, Debra J.
Hallford, David J.
and
Watsford, Clare
2022.
Structured data vs. unstructured data in machine learning prediction models for suicidal behaviors: A systematic review and meta-analysis.
Frontiers in Digital Health,
Vol. 4,
Issue. ,
Holling, Heinz
Jansen, Katrin
Böhning, Walailuck
Böhning, Dankmar
Martin, Susan
and
Sangnawakij, Patarawan
2022.
Estimation of Effect Heterogeneity in Rare Events Meta-Analysis.
Psychometrika,
Vol. 87,
Issue. 3,
p.
1081.
Sehovic, Emir
Urru, Sara
Chiorino, Giovanna
and
Doebler, Philipp
2022.
Meta-analysis of diagnostic cell-free circulating microRNAs for breast cancer detection.
BMC Cancer,
Vol. 22,
Issue. 1,
Luo, Chongliang
Marks‐Anglin, Arielle
Duan, Rui
Lin, Lifeng
Hong, Chuan
Chu, Haitao
and
Chen, Yong
2022.
Accounting for publication bias using a bivariate trim and fill meta‐analysis procedure.
Statistics in Medicine,
Vol. 41,
Issue. 18,
p.
3466.
Holling, Heinz
and
Jansen, Katrin
2023.
Quantitative Psychology.
Vol. 422,
Issue. ,
p.
197.
Lee, Jenny
van Es, Nick
Takada, Toshihiko
Klok, Frederikus A.
Geersing, Geert-Jan
Blume, Jeffrey
and
Bossuyt, Patrick M.
2023.
Covariate-specific ROC curve analysis can accommodate differences between covariate subgroups in the evaluation of diagnostic accuracy.
Journal of Clinical Epidemiology,
Vol. 160,
Issue. ,
p.
14.
Babačić, Haris
Christ, Wanda
Araújo, José Eduardo
Mermelekas, Georgios
Sharma, Nidhi
Tynell, Janne
García, Marina
Varnaite, Renata
Asgeirsson, Hilmir
Glans, Hedvig
Lehtiö, Janne
Gredmark-Russ, Sara
Klingström, Jonas
and
Pernemalm, Maria
2023.
Comprehensive proteomics and meta-analysis of COVID-19 host response.
Nature Communications,
Vol. 14,
Issue. 1,
Sangnawakij, Patarawan
Böhning, Dankmar
Holling, Heinz
and
Jansen, Katrin
2024.
Nonparametric estimation of the random effects distribution for the risk or rate ratio in rare events meta‐analysis with the arm‐based and contrast‐based approaches.
Statistics in Medicine,
Vol. 43,
Issue. 4,
p.
706.
Garaba, Alexandru
Aslam, Nummra
Ponzio, Francesco
Panciani, Pier Paolo
Brinjikji, Waleed
Fontanella, Marco
and
De Maria, Lucio
2024.
Radiomics for differentiation of gliomas from primary central nervous system lymphomas: a systematic review and meta-analysis.
Frontiers in Oncology,
Vol. 14,
Issue. ,
Guedj, Danaé
Neveü, Sophie
Becker, Minerva
and
Mermod, Maxime
2024.
FDG PET-CT for the Detection of Occult Nodal Metastases in Head and Neck Cancer: A Systematic Review and Meta-Analysis.
Cancers,
Vol. 16,
Issue. 17,
p.
2954.
De Maria, Lucio
Ponzio, Francesco
Cho, Hwan-ho
Skogen, Karoline
Tsougos, Ioannis
Gasparini, Mauro
Zeppieri, Marco
Ius, Tamara
Ugga, Lorenzo
Panciani, Pier Paolo
Fontanella, Marco Maria
Brinjikji, Waleed
and
Agosti, Edoardo
2024.
The Current Diagnostic Performance of MRI-Based Radiomics for Glioma Grading: A Meta-Analysis.
Journal of Integrative Neuroscience,
Vol. 23,
Issue. 5,
Granieri, Stefano
Altomare, Michele
Bonomi, Alessandro
Panagini, Giada
Frassini, Simone
Cioffi, Stefano Piero Bernardo
Basta, Giorgio
Spota, Andrea
Sammartano, Fabrizio
Bini, Roberto
Renzi, Federica
Reitano, Elisa
Chiara, Osvaldo
and
Cimbanassi, Stefania
2024.
Contrast-enhanced CT scan (CECT) for the detection of hollow viscus and mesenteric injuries in blunt trauma - an updated systematic review of the literature and meta-analysis of diagnostic test accuracy.
European Journal of Trauma and Emergency Surgery,
Vol. 50,
Issue. 6,
p.
2709.
Müller, Katharina J.
Schmidbauer, Moritz L.
Schönecker, Sonja
Kamm, Katharina
Pelz, Johann O.
Holzapfel, Korbinian
Papadopoulou, Marianna
Bakola, Eleni
Tsivgoulis, Georgios
Naumann, Markus
Hermann, Andreas
Walter, Uwe
Dimitriadis, Konstantinos
Reilich, Peter
and
Schöberl, Florian
2024.
Diagnostic accuracy and confounders of vagus nerve ultrasound in amyotrophic lateral sclerosis—a single-center case series and pooled individual patient data meta-analysis.
Journal of Neurology,
Vol. 271,
Issue. 9,
p.
6255.
Ganzenmüller, Johanna Louise
Ballmann, Cora
von Nessen-Lapp, Regina Margarethe Wehrstedt
Schulze, Marcel
Sanftenberg, Linda
Berger, Mathias
Philipsen, Alexandra
and
Gensichen, Jochen
2024.
Screening tools for adult ADHD patients in primary care.
Journal of Affective Disorders Reports,
Vol. 17,
Issue. ,
p.
100800.
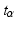 transformation, a flexible family of transformations for proportions. A collection of SROC curves is constructed that approximately contains the Lehmann family but in addition allows the modeling of shapes beyond the Lehmann ROC curves. We introduce two rationales for determining the shape from the data. Using the fact that each curve corresponds to a natural univariate measure of diagnostic accuracy, we show how covariate adjusted mixtures lead to a meta-regression on SROC curves. Three worked examples illustrate the method.
transformation, a flexible family of transformations for proportions. A collection of SROC curves is constructed that approximately contains the Lehmann family but in addition allows the modeling of shapes beyond the Lehmann ROC curves. We introduce two rationales for determining the shape from the data. Using the fact that each curve corresponds to a natural univariate measure of diagnostic accuracy, we show how covariate adjusted mixtures lead to a meta-regression on SROC curves. Three worked examples illustrate the method.

