1 results
ON THE CROSSING NUMBER OF THE CARTESIAN PRODUCT OF A SUNLET GRAPH AND A STAR GRAPH
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 08 February 2019, pp. 5-12
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
-
The exact crossing number is only known for a small number of families of graphs. Many of the families for which crossing numbers have been determined correspond to cartesian products of two graphs. Here, the cartesian product of the sunlet graph, denoted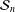
${\mathcal{S}}_{n}$, and the star graph, denoted 
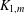$K_{1,m}$, is considered for the first time. It is proved that the crossing number of 
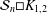${\mathcal{S}}_{n}\Box K_{1,2}$ is 
$n$, and the crossing number of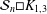 
${\mathcal{S}}_{n}\Box K_{1,3}$ is 
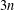$3n$. An upper bound for the crossing number of 
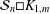${\mathcal{S}}_{n}\Box K_{1,m}$ is also given.
