Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-28T00:28:05.763Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE CROSSING NUMBER OF THE CARTESIAN PRODUCT OF A SUNLET GRAPH AND A STAR GRAPH

Part of: Graph theory Discrete mathematics in relation to computer science

Published online by Cambridge University Press:  08 February 2019

MICHAEL HAYTHORPE Open the ORCID record for MICHAEL HAYTHORPE [Opens in a new window]  and
ALEX NEWCOMBE Open the ORCID record for ALEX NEWCOMBE [Opens in a new window]
MICHAEL HAYTHORPE*
Affiliation:
1284 South Road, Clovelly Park, 5042, College of Science and Engineering, Flinders University, Australia email michael.haythorpe@flinders.edu.au
ALEX NEWCOMBE
Affiliation:
1284 South Road, Clovelly Park, 5042, College of Science and Engineering, Flinders University, Australia email alex.newcombe@flinders.edu.au
*
✉michael.haythorpe@flinders.edu.au
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The exact crossing number is only known for a small number of families of graphs. Many of the families for which crossing numbers have been determined correspond to cartesian products of two graphs. Here, the cartesian product of the sunlet graph, denoted 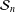${\mathcal{S}}_{n}$, and the star graph, denoted 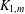$K_{1,m}$, is considered for the first time. It is proved that the crossing number of 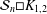${\mathcal{S}}_{n}\Box K_{1,2}$ is $n$, and the crossing number of 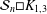${\mathcal{S}}_{n}\Box K_{1,3}$ is 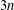$3n$. An upper bound for the crossing number of 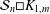${\mathcal{S}}_{n}\Box K_{1,m}$ is also given.

Keywords

crossing numbercartesian productstarsunlet graph

MSC classification

Primary: 05C10: Planar graphs; geometric and topological aspects of graph theory
Secondary: 68R10: Graph theory (including graph drawing)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 1 , August 2019 , pp. 5 - 12
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

References

Ábrego, B. M., Aichholzer, O., Fernández-Merchant, S., Hackl, T., Pammer, J., Pilz, A., Ramos, P., Salazar, G. and Vogtenhuber, B., ‘All good drawings of small complete graphs’, in: Proc. 31st European Workshop on Computational Geometry (EuroCG) 2015, Book of Abstracts , eurocg15.fri.uni-lj.si/pub/eurocg15-book-of-abstracts.pdf, 57–60.Google Scholar
Anderson, M., Richter, R. B. and Rodney, P., ‘The crossing number of C 6 × C 6 ’, Congr. Numer. 117 (1996), 97–107.Google Scholar
Anderson, M., Richter, R. B. and Rodney, P., ‘The crossing number of C 7 × C 7 ’, Congr. Numer. 125 (1996), 97–117.Google Scholar
Asano, K., ‘The crossing number of K 1, 3, n and K 2, 3, n ’, J. Graph Theory 10 (1986), 1–8.Google Scholar
Beineke, L. W. and Ringeisen, R. D., ‘On the crossing numbers of products of cycles and graphs of order four’, J. Graph Theory 4(2) (1980), 145–155.Google Scholar
Bokal, D., ‘On the crossing number of Cartesian products with paths’, J. Combin. Theory Ser. B 97(3) (2007), 381–384.Google Scholar
Cabello, S. and Mohar, B., ‘Adding one edge to planar graphs makes crossing number and 1-planarity hard’, SIAM J. Comput. 42(5) (2013), 1803–1829.Google Scholar
Chimani, M. and Wiedera, T., ‘An ILP-based proof system for the crossing number problem’, in: 24th European Symposium on Algorithms (ESA 2016), Aarhus, Denmark, Leibniz International Proceedings in Informatics, 56 (Schloss Dagstuhl, Dagstuhl, Germany, 2016), 29.1–29.13.Google Scholar
Clancy, K., Haythorpe, M. and Newcombe, A., ‘An effective crossing minimisation heuristic based on star insertion’, preprint available at arXiv:abs/1804.09900.Google Scholar
Dean, A. M. and Richter, R. B., ‘The crossing number of C 4 × C 4 ’, J. Graph Theory 19(1) (1995), 125–129.Google Scholar
Garey, M. R. and Johnson, D. S., ‘Crossing number is NP-complete’, SIAM J. Algebr. Discrete Methods 4(3) (1983), 312–316.Google Scholar
Glebsky, L. Y. and Salazar, G., ‘The crossing number of C m × C n is as conjectured for n ≥ m (m + 1)’, J. Graph Theory 47(1) (2004), 53–72.Google Scholar
Harary, F., Kainen, P. C. and Schwenk, A. J., ‘Toroidal graphs with arbitrarily high crossing numbers’, Nanta Math. 6(1) (1973), 58–67.Google Scholar
Jendrol, S. and Šcerbová, M., ‘On the crossing numbers of S m × P n and S m × C n ’, Casopis pro Pestováni Mat. 107 (1982), 225–230.Google Scholar
Klešč, M., ‘On the crossing numbers of Cartesian products of stars and paths or cycles’, Math. Slovaca 41(2) (1991), 113–120.Google Scholar
Klešč, M. and Kravecová, D., ‘The crossing number of P n 2◻C 3 ’, Discrete Math. 312 (2012), 2096–2101.Google Scholar
Klešč, M., Petrillová, J. and Valo, M., ‘On the crossing numbers of cartesian products of wheels and trees’, Discrete Math. Graph Theory 37(2) (2017), 399–413.Google Scholar
McQuillan, D., Pan, S. and Richter, R. B., ‘On the crossing number of K 13 ’, J. Combin. Theory Ser. B 115 (2015), 224–235.Google Scholar
Richter, R. B. and Thomassen, C., ‘Intersections of curve systems and the crossing number of C 5 × C 5 ’, Discrete Comput. Geom. 13(1) (1995), 149–159.Google Scholar
Ringeisen, R. D. and Beineke, L. W., ‘The crossing number of C 3 × C n ’, J. Combin. Theory Ser. B 24(2) (1978), 134–136.Google Scholar
Zheng, W., Lin, X., Yang, Y. and Deng, C., ‘On the crossing number of K m ◻C n and K m, l ◻P n ’, Discrete Appl. Math. 156 (2008), 1892–1907.Google Scholar