We find a non-displaceable Lagrangian torus fiber in a semi-toric system which is superheavy with respect to a certain symplectic quasi-state. The proof employs both 4-dimensional techniques and those from symplectic field theory. In particular, our result implies Lagrangian 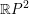 $\mathbb{R}P^{2}$ is not a stem in
$\mathbb{R}P^{2}$ is not a stem in 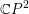 $\mathbb{C}P^{2}$, answering a question of Entov and Polterovich.
$\mathbb{C}P^{2}$, answering a question of Entov and Polterovich.
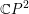 $\mathbb{C}P^{2}$
$\mathbb{C}P^{2}$