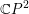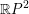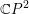Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
de Velloso Vianna, Renato Ferreira
2016.
Infinitely many exotic monotone Lagrangian tori in ℂℙ2.
Journal of Topology,
Vol. 9,
Issue. 2,
p.
535.
Oakley, Joel
and
Usher, Michael
2016.
On certain Lagrangian submanifolds of S2×S2 and ℂPn.
Algebraic & Geometric Topology,
Vol. 16,
Issue. 1,
p.
149.
Vianna, Renato
2017.
Infinitely many monotone Lagrangian tori in del Pezzo surfaces.
Selecta Mathematica,
Vol. 23,
Issue. 3,
p.
1955.
Leclercq, Rémi
and
Zapolsky, Frol
2018.
Spectral invariants for monotone Lagrangians.
Journal of Topology and Analysis,
Vol. 10,
Issue. 03,
p.
627.
Fukaya, Kenji
Oh, Yong-Geun
Ohta, Hiroshi
and
Ono, Kaoru
2020.
Kuranishi Structures and Virtual Fundamental Chains.
p.
1.
Sun, Yuhan
2020.
An-type surface singularity and nondisplaceable Lagrangian tori.
International Journal of Mathematics,
Vol. 31,
Issue. 03,
p.
2050020.
Kawasaki, Morimichi
and
Orita, Ryuma
2021.
Disjoint superheavy subsets and fragmentation norms.
Journal of Topology and Analysis,
Vol. 13,
Issue. 02,
p.
443.
Borman, Matthew Strom
Sheridan, Nick
and
Varolgunes, Umut
2022.
Quantum cohomology as a deformation of symplectic cohomology.
Journal of Fixed Point Theory and Applications,
Vol. 24,
Issue. 2,
KAWASAKI, Morimichi
and
ORITA, Ryuma
2022.
Rigid fibers of integrable systems on cotangent bundles.
Journal of the Mathematical Society of Japan,
Vol. 74,
Issue. 3,
Shelukhin, Egor
Tonkonog, Dmitry
and
Vianna, Renato
2024.
Geometry of symplectic flux and Lagrangian torus fibrations.
Journal of Topology,
Vol. 17,
Issue. 4,
Brendel, Joé
2025.
Local exotic tori.
Transactions of the American Mathematical Society,
Vol. 378,
Issue. 6,
p.
4369.