A word u defined over an alphabet $\mathcal A$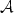 is c-balanced (c∈$\mathbb N$
is c-balanced (c∈$\mathbb N$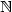 ) if for all pairs of factors v, w of u of the same length
and for all letters a∈$\mathcal A$
) if for all pairs of factors v, w of u of the same length
and for all letters a∈$\mathcal A$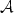 , the difference between the number of letters a in v and w is less or equal to c. In this paper we consider a ternary alphabet
$\mathcal A$
, the difference between the number of letters a in v and w is less or equal to c. In this paper we consider a ternary alphabet
$\mathcal A$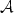 = {L, S, M} and a class of substitutions $\varphi_p$
= {L, S, M} and a class of substitutions $\varphi_p$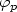 defined by $\varphi_p$
defined by $\varphi_p$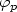 (L) = LpS, $\varphi_p$
(L) = LpS, $\varphi_p$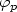 (S) = M,
$\varphi_p$
(S) = M,
$\varphi_p$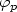 (M) = Lp–1S where p> 1.
We prove that the fixed point of $\varphi_p$
(M) = Lp–1S where p> 1.
We prove that the fixed point of $\varphi_p$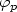 , formally written as $\varphi_p^\infty$
, formally written as $\varphi_p^\infty$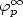 (L), is 3-balanced and that its Abelian complexity is bounded above by the value 7, regardless of the value of p. We also show that both these bounds are optimal, i.e. they cannot be improved.
(L), is 3-balanced and that its Abelian complexity is bounded above by the value 7, regardless of the value of p. We also show that both these bounds are optimal, i.e. they cannot be improved.