1 results
The Galvin property under the ultrapower axiom
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 27 May 2024, pp. 1-32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
We continue the study of the Galvin property from Benhamou, Garti, and Shelah (2023, Proceedings of the American Mathematical Society 151, 1301–1309) and Benhamou (2023, Saturation properties in canonical inner models, submitted). In particular, we deepen the connection between certain diamond-like principles and non-Galvin ultrafilters. We also show that any Dodd sound non p-point ultrafilter is non-Galvin. We use these ideas to formulate what appears to be the optimal large cardinal hypothesis implying the existence of a non-Galvin ultrafilter, improving on a result from Benhamou and Dobrinen (2023, Journal of Symbolic Logic, 1–34). Finally, we use a strengthening of the Ultrapower Axiom to prove that in all the known canonical inner models, a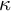
$\kappa $-complete ultrafilter has the Galvin property if and only if it is an iterated sum of p-points.
