We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this paper we prove two results concerning Vinogradov’s three primes theorem with primes that can be called almost twin primes. First, for any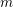 
$m$, every sufficiently large odd integer 
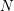$N$ can be written as a sum of three primes 
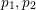$p_{1},p_{2}$ and 
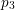$p_{3}$ such that, for each 
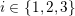$i\in \{1,2,3\}$, the interval 
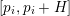$[p_{i},p_{i}+H]$ contains at least 
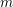$m$ primes, for some 
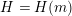$H=H(m)$. Second, every sufficiently large integer 
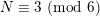$N\equiv 3~(\text{mod}~6)$ can be written as a sum of three primes 
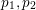$p_{1},p_{2}$ and 
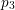$p_{3}$ such that, for each 
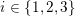$i\in \{1,2,3\}$, 
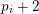$p_{i}+2$ has at most two prime factors.
