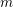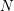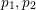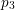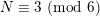Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Tolev, D. I.
2017.
On a Diophantine Inequality with Prime Numbers of a Special Type.
Proceedings of the Steklov Institute of Mathematics,
Vol. 299,
Issue. 1,
p.
246.
Teräväinen, Joni
2018.
THE GOLDBACH PROBLEM FOR PRIMES THAT ARE SUMS OF TWO SQUARES PLUS ONE.
Mathematika,
Vol. 64,
Issue. 1,
p.
20.
Dimitrov, Stoyan
2018.
Diophantine approximation by special primes.
Vol. 2048,
Issue. ,
p.
050005.
Maynard, James
2019.
The twin prime conjecture.
Japanese Journal of Mathematics,
Vol. 14,
Issue. 2,
p.
175.
Grimmelt, Lasse
2022.
Vinogradov’s theorem with Fouvry–Iwaniec
primes.
Algebra & Number Theory,
Vol. 16,
Issue. 7,
p.
1705.
Li, Jinjiang
Zhang, Min
and
Xue, Fei
2022.
On a ternary Diophantine equation involving fractional powers with prime variables of a special form.
The Ramanujan Journal,
Vol. 58,
Issue. 4,
p.
1171.
Li, Jinjiang
Xue, Fei
and
Zhang, Min
2022.
A ternary Diophantine inequality with prime numbers of a special form.
Periodica Mathematica Hungarica,
Vol. 85,
Issue. 1,
p.
14.
Bienvenu, Pierre-Yves
Shao, Xuancheng
and
Teräväinen, Joni
2023.
A transference principle for systems of linear equations, and applications to almost twin primes.
Algebra & Number Theory,
Vol. 17,
Issue. 2,
p.
497.
Bienvenu, Pierre-Yves
Shao, Xuancheng
and
Teräväinen, Joni
2023.
A transference principle for systems of linear equations, and applications to almost twin primes.
Algebra & Number Theory,
Vol. 17,
Issue. 2,
p.
497.
Matomäki, Kaisa
and
Teräväinen, Joni
2024.
Products of primes in arithmetic progressions.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 0,
Issue. 0,
Wu, Liuying
2024.
On a Diophantine equation involving fractional powers with primes of special types.
AIMS Mathematics,
Vol. 9,
Issue. 6,
p.
16486.
Li, Jinjiang
Xue, Fei
and
Zhang, Min
2024.
A quaternary Diophantine inequality with prime numbers of a special form.
The Ramanujan Journal,
Vol. 63,
Issue. 2,
p.
259.
Sun, Yu-Chen
Du, Shan-Shan
and
Pan, Hao
2025.
Vinogradov’s Theorem with Piatetski-Shapiro Primes.
International Mathematics Research Notices,
Vol. 2025,
Issue. 15,
Leng, James
and
Sawhney, Mehtaab
2025.
Vinogradov’s Theorem for Primes With Restricted Digits.
International Mathematics Research Notices,
Vol. 2025,
Issue. 3,