We consider a discrete-time population growth system called the Bienaymé–Galton–Watson stochastic branching system. We deal with a noncritical case, in which the per capita offspring mean $m\neq1$. The famous Kolmogorov theorem asserts that the expectation of the population size in the subcritical case $m<1$ on positive trajectories of the system asymptotically stabilizes and approaches ${1}/\mathcal{K}$, where $\mathcal{K}$ is called the Kolmogorov constant. The paper is devoted to the search for an explicit expression of this constant depending on the structural parameters of the system. Our argumentation is essentially based on the basic lemma describing the asymptotic expansion of the probability-generating function of the number of individuals. We state this lemma for the noncritical case. Subsequently, we find an extended analogue of the Kolmogorov constant in the noncritical case. An important role in our discussion is also played by the asymptotic properties of transition probabilities of the Q-process and their convergence to invariant measures. Obtaining the explicit form of the extended Kolmogorov constant, we refine several limit theorems of the theory of noncritical branching systems, showing explicit leading terms in the asymptotic expansions.

Customer churn, which insurance companies use to describe the non-renewal of existing customers, is a widespread and expensive problem in general insurance, particularly because contracts are usually short-term and are renewed periodically. Traditionally, customer churn analyses have employed models which utilise only a binary outcome (churn or not churn) in one period. However, real business relationships are multi-period, and policyholders may reside and transition between a wider range of states beyond that of the simply churn/not churn throughout this relationship. To better encapsulate the richness of policyholder behaviours through time, we propose multi-state customer churn analysis, which aims to model behaviour over a larger number of states (defined by different combinations of insurance coverage taken) and across multiple periods (thereby making use of readily available longitudinal data). Using multinomial logistic regression (MLR) with a second-order Markov assumption, we demonstrate how multi-state customer churn analysis offers deeper insights into how a policyholder’s transition history is associated with their decision making, whether that be to retain the current set of policies, churn, or add/drop a coverage. Applying this model to commercial insurance data from the Wisconsin Local Government Property Insurance Fund, we illustrate how transition probabilities between states are affected by differing sets of explanatory variables and that a multi-state analysis can potentially offer stronger predictive performance and more accurate calculations of customer lifetime value (say), compared to the traditional customer churn analysis techniques.

Precision agriculture technologies have been adopted individually and in bundles. A sample of 348 Kansas Farm Management Association farm-level observations provides insight into technology adoption patterns of precision agriculture technologies. Estimated transition probabilities shed light on how adoption paths lead to bundling of technologies. Three information intensive technologies were assigned to one of eight possible bundles, and the sequence of adoption was examined using Markov transition processes. The probability that farms remain with the same bundle or transition to a different bundle by the next time period are reported. Farms with the complete bundle of all three technologies were likely to persist with their current technology.

Observer-based studies often underestimate key ecological parameters. Here a fresh approach was used to analyse six years (2006–11) of attendance cycles to estimate foraging trip lengths of a lactating flipper-tagged otariid: subantarctic fur seals at Marion Island. Multi-state mark-recapture models were used to calculate detection failures of females, correct estimates accordingly, and investigate the effects of year, season, pup sex and the presence of a telemetry device on attendance cycle parameters. There were no differences between corrected and uncorrected attendance data. This is attributed to the high capture probability across all seasons (range: 83–98%). This illustrates that observer-based studies are useful to augment telemetry studies. Only season and pup sex had a significant impact on female provisioning rates. In winter, foraging trip durations were longer (t-value=25.22, P<0.0001) and attendance durations shorter (t-value=-2.15, P=0.01) than during summer. Females with female pups spent a higher proportion of their time on land (χ2=6.6, P<0.05). Male pups have higher growth demands and are larger which suggests they can deplete female milk-stores faster.

This is the first of two papers in which we estimate transition probabilities amongst levels of disability as defined in the Australian Survey of Disability, Ageing and Carers. In this paper we describe both the main tools of our estimation and the estimation of the numbers of individuals in different disability categories at annual intervals using survey data that are available at five year intervals. In Paper II we describe our estimation procedure, followed by its implementation, discussion of results and graduation of the estimated transition probabilities.

This is the second of two papers in which we estimate transition probabilities amongst levels of disability as defined in the Australian Survey of Disability, Ageing and Carers. In this paper we describe our estimation procedure, followed by its implementation, discussion of results and graduation of the estimated transition probabilities.

We investigate the asymptotical behaviour of the transition probabilities of the simple random walk on the 2-comb. In particular, we obtain space-time uniform asymptotical estimates which show the lack of symmetry of this walk better than local limit estimates. Our results also point out the impossibility of getting sub-Gaussian estimates involving the spectral and walk dimensions of the graph.

Let N(t) be an exponentially ergodic birth-death process on the state space {0, 1, 2, ···} governed by the parameters {λn, μn}, where µ0 = 0, such that λn = λ and μn = μ for all n ≧ N, N ≧ 1, with λ < μ. In this paper, we develop an algorithm to determine the decay parameter of such a specialized exponentially ergodic birth-death process, based on van Doorn's representation (1987) of eigenvalues of sign-symmetric tridiagonal matrices. The decay parameter is important since it is indicative of the speed of convergence to ergodicity. Some comparability results for the decay parameters are given, followed by the discussion for the decay parameter of a birth-death process governed by the parameters such that limn→∞λn = λ and limn→∞µn = μ. The algorithm is also shown to be a useful tool to determine the quasi-stationary distribution, i.e. the limiting distribution conditioned to stay in {1, 2, ···}, of such specialized birth-death processes.

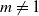
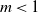
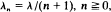Exact expressions are derived for the transition probabilities of the birth-death process with parameters and 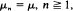which serves as a queueing model where potential customers are discouraged by queue length.