Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chihara, Theodore S.
and
Ismail, Mourad E.H.
1982.
Orthogonal polynomials suggested by a queueing model.
Advances in Applied Mathematics,
Vol. 3,
Issue. 4,
p.
441.
Conolly, B. W.
1983.
More transient results for generalised state-dependent Erlangian queues.
Advances in Applied Probability,
Vol. 15,
Issue. 03,
p.
688.
Ismail, Mourad E.H
1985.
A queueing model and a set of orthogonal polynomials.
Journal of Mathematical Analysis and Applications,
Vol. 108,
Issue. 2,
p.
575.
Montazer-Haghighi, A.
Medhi, J.
and
Mohanty, S.G.
1986.
On a multiserver markovian queueing system with balking and reneging.
Computers & Operations Research,
Vol. 13,
Issue. 4,
p.
421.
Chihara, Laura M
and
Chihara, T.S
1987.
A class of nonsymmetric orthogonal polynomials.
Journal of Mathematical Analysis and Applications,
Vol. 126,
Issue. 1,
p.
275.
Zeifman, A. I.
1991.
Some estimates of the rate of convergence for birth and death processes.
Journal of Applied Probability,
Vol. 28,
Issue. 02,
p.
268.
Zeifman, A. I.
1991.
Qualitative properties of inhomogeneous birth and death processes.
Journal of Soviet Mathematics,
Vol. 57,
Issue. 4,
p.
3217.
Browne, Sid
and
Sigman, Karl
1992.
Work-modulated queues with applications to storage processes.
Journal of Applied Probability,
Vol. 29,
Issue. 03,
p.
699.
Sharma, O.P.
and
Maheswar, M.V.R.
1993.
Transient behaviour of a simple queue with discouraged arrivals.
Optimization,
Vol. 27,
Issue. 3,
p.
283.
Van Assche, Walter
1996.
Compact Jacobi matrices : from Stieltjes to Krein and M(a,b).
Annales de la Faculté des sciences de Toulouse : Mathématiques,
Vol. S5,
Issue. ,
p.
195.
Granovsky, B. L.
and
Zeifman, A. I.
2000.
Nonstationary Markovian queues.
Journal of Mathematical Sciences,
Vol. 99,
Issue. 4,
p.
1415.
Coolen-Schrijner, Pauline
and
Van Doorn, Erik A.
2001.
On the convergence to stationarity of birth-death processes.
Journal of Applied Probability,
Vol. 38,
Issue. 03,
p.
696.
Coolen-Schrijner, Pauline
and
Van Doorn, Erik A.
2001.
On the convergence to stationarity of birth-death processes.
Journal of Applied Probability,
Vol. 38,
Issue. 3,
p.
696.
Askey, R.
Ismail, M.E.H.
and
Van Assche, W.
2001.
Ted Chihara and his work on orthogonal polynomials.
Journal of Computational and Applied Mathematics,
Vol. 133,
Issue. 1-2,
p.
1.
Bitran, Gabriel
and
Caldentey, René
2002.
Two-Class Priority Queueing System with State-Dependent Arrivals.
Queueing Systems,
Vol. 40,
Issue. 4,
p.
355.
Granovsky, Boris L.
and
Zeifman, A.
2004.
Nonstationary Queues: Estimation of the Rate of Convergence.
Queueing Systems,
Vol. 46,
Issue. 3-4,
p.
363.
2004.
Birth and Death (BDP) Process Models with Applications.
American Journal of Mathematical and Management Sciences,
Vol. 24,
Issue. 1-2,
p.
1.
Zeifman, A. I.
and
Satin, Ya. A.
2007.
Mean characteristics of Markov queueing systems.
Automation and Remote Control,
Vol. 68,
Issue. 9,
p.
1583.
Белорусов, Тимофей Николаевич
and
Belorusov, Timophey Nikolaevich
2011.
Эргодичность многоканальной системы обслуживания с возможностью неприсоединения к очереди.
Теория вероятностей и ее применения,
Vol. 56,
Issue. 1,
p.
145.
Ammar, S. I.
El-Sherbiny, A. A.
El-Shehawy, S. A.
and
Al-Seedy, R. O.
2012.
A matrix approach for the transient solution of an M/M/1/N queue with discouraged arrivals and reneging.
International Journal of Computer Mathematics,
Vol. 89,
Issue. 4,
p.
482.

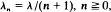 and
and 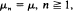 which serves as a queueing model where potential customers are discouraged by queue length.
which serves as a queueing model where potential customers are discouraged by queue length.