The ergodic properties of two uncoupled oscillators, one horizontal and one vertical, residing in a class of non-rectangular star-shaped polygons with only vertical and horizontal boundaries and impacting elastically from its boundaries are studied. We prove that the iso-energy level sets topology changes non-trivially; the flow on level sets is always conjugated to a translation flow on a translation surface, yet, for some segments of partial energies the genus of the surface is strictly greater than 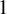$1$ . When at least one of the oscillators is unharmonic, or when both are harmonic and non-resonant, we prove that for almost all partial energies, including the impacting ones, the flow on level sets is uniquely ergodic. When both oscillators are harmonic and resonant, we prove that there exist intervals of partial energies on which periodic ribbons and additional ergodic components coexist. We prove that for almost all partial energies in such segments the motion is uniquely ergodic on the part of the level set that is not occupied by the periodic ribbons. This implies that ergodic averages project to piecewise smooth weighted averages in the configuration space.

In this paper we prove that the set of translation structures for which the corresponding vertical translation flows are disjoint with its inverse contains a $G_{\unicode[STIX]{x1D6FF}}$-dense subset in every non-hyperelliptic connected component of the moduli space ${\mathcal{M}}$. This is in contrast to hyperelliptic case, where for every translation structure the associated vertical flow is reversible, i.e., it is isomorphic to its inverse by an involution. To prove the main result, we study limits of the off-diagonal 3-joinings of special representations of vertical translation flows. Moreover, we construct a locally defined continuous embedding of the moduli space into the space of measure-preserving flows to obtain the $G_{\unicode[STIX]{x1D6FF}}$-condition. Moreover, as a by-product we get that in every non-hyperelliptic connected component of the moduli space there is a dense subset of translation structures whose vertical flow is reversible.

For a $ \mathbb{Z} $-cover $\widetilde {M} \rightarrow M$ of a translation surface, which is a lattice surface, and which admits infinite strips, we prove that almost every direction for the straightline flow is ergodic.