Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T13:37:50.025Z Has data issue: false hasContentIssue false
  • English
  • Français

ON TYPICALITY OF TRANSLATION FLOWS WHICH ARE DISJOINT WITH THEIR INVERSE

Part of: Ergodic theory Low-dimensional dynamical systems Smooth dynamical systems: general theory

Published online by Cambridge University Press:  11 December 2018

Przemysław Berk ,
Krzysztof Frączek  and
Thierry de la Rue
Przemysław Berk
Affiliation:
Faculty of Mathematics and Computer Science, Nicolaus Copernicus University, ul. Chopina 12/18, 87-100 Toruń, Poland (zimowy@mat.umk.pl; fraczek@mat.umk.pl)
Krzysztof Frączek
Affiliation:
Faculty of Mathematics and Computer Science, Nicolaus Copernicus University, ul. Chopina 12/18, 87-100 Toruń, Poland (zimowy@mat.umk.pl; fraczek@mat.umk.pl)
Thierry de la Rue
Affiliation:
Laboratoire de Mathématiques Raphaël Salem, Normandie Université, Université de Rouen, CNRS, Avenue de l’Université, 76801 Saint Etienne du Rouvray, France (Thierry.de-la-Rue@univ-rouen.fr)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we prove that the set of translation structures for which the corresponding vertical translation flows are disjoint with its inverse contains a 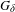$G_{\unicode[STIX]{x1D6FF}}$-dense subset in every non-hyperelliptic connected component of the moduli space 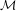${\mathcal{M}}$. This is in contrast to hyperelliptic case, where for every translation structure the associated vertical flow is reversible, i.e., it is isomorphic to its inverse by an involution. To prove the main result, we study limits of the off-diagonal 3-joinings of special representations of vertical translation flows. Moreover, we construct a locally defined continuous embedding of the moduli space into the space of measure-preserving flows to obtain the 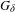$G_{\unicode[STIX]{x1D6FF}}$-condition. Moreover, as a by-product we get that in every non-hyperelliptic connected component of the moduli space there is a dense subset of translation structures whose vertical flow is reversible.

Keywords

measure-preserving flowstranslation surfacesreversibility of dynamical systemsjoinings methods in ergodic theory

MSC classification

Primary: 37A10: One-parameter continuous families of measure-preserving transformations 37E35: Flows on surfaces
Secondary: 37C80: Symmetries, equivariant dynamical systems
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 5 , September 2020 , pp. 1677 - 1737
Check for updates
Copyright
© Cambridge University Press 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ambrose, W., Representation of ergodic flows, Ann. of Math. (2) 42 (1941), 723–739.Google Scholar
Avila, A. and Forni, G., Weak mixing for interval exchange transformations and translation flows, Ann. of Math. (2) 165 (2007), 637–664.Google Scholar
Berk, P. and Frączek, K., On special flows that are not isomorphic to their inverses, Discrete Contin. Dyn. Syst. 35 (2015), 829–855.Google Scholar
Danilenko, A. I. and Ryzhikov, V.V., On self-similarities of ergodic flows, Proc. Lond. Math. Soc. 104 (2012), 431–454.Google Scholar
del Junco, A., Disjointness of measure-preserving transformations, minimal self-joinings and category, in Ergodic Theory and Dynamical Systems, I (College Park, Md., 1979–80), Progress in Mathematics, Volume 10, pp. 81–89 (Birkhäuser, Boston, Mass, 1981).Google Scholar
Fox, R. H. and Kershner, R. B., Concerning the transitive properties of geodesics on a rational polyhedron, Duke Math. J. 2 (1936), 147–150.Google Scholar
Frączek, K., Density of mild mixing property for vertical flows of Abelian differentials, Proc. Amer. Math. Soc. 137 (2009), 4129–4142.Google Scholar
Frączek, K., Kułaga-Przymus, J. and Lemańczyk, M., Non-reversibility and self-joinings of higher orders for ergodic flows, J. Anal. Math. 122 (2014), 163–227.Google Scholar
Glasner, E., Ergodic Theory Via Joinings, Mathematical Surveys and Monographs, Volume 101 (American Mathematical Society, Providence, RI, 2003).Google Scholar
Goffman, C. and Pedrick, G., A proof of the homeomorphism of Lebesgue-Stieltjes measure with Lebesgue measure, Proc. Amer. Math. Soc. 52 (1975), 196–198.Google Scholar
Halmos, P. R., Ergodic Theory (Chelsea, New York, 1956).Google Scholar
Katok, A. B., Interval exchange transformations and some special flows are not mixing, Israel J. Math. 35 (1980), 301–310.Google Scholar
Katok, A. B. and Zemljakov, A. N., Topological transitivity of billiards in polygons, Mat. Zametki 18 (1975), 291–300.Google Scholar
King, J., Joining-rank and the structure of finite rank mixing transformations, J. Anal. Math. 51 (1988), 182–227.Google Scholar
Khinchin, A. Y., Continued Fractions (The University of Chicago Press, Chicago-London, 1964).Google Scholar
Kontsevich, M. and Zorich, A., Connected components of the moduli spaces of Abelian differentials with prescribed singularities, Invent. Math. 153 (2003), 631–678.Google Scholar
Masur, H., Interval exchange transformations and measured foliations, Ann. of Math. (2) 115 (1982), 169–200.Google Scholar
Moser, J., On the volume elements on a manifold, Trans. Amer. Math. Soc. 120 (1965), 286–294.Google Scholar
Rauzy, G., Échanges d’intervalles et transformations induites, Acta Arith. 34 (1979), 315–328.Google Scholar
Ryzhikov, V. V., Partial multiple mixing on subsequences can distinguish between automorphisms T and T -1, Math. Notes 74 (2003), 841–847.Google Scholar
Srivastava, S. M., A course on Borel sets, Graduate Texts in Mathematics, Volume 180 (Springer, New York, 1998).Google Scholar
Veech, W. A., Gauss measures for transformations on the space of interval exchange maps, Ann. of Math. (2) 115 (1982), 201–242.Google Scholar
Vorobets, Ya., Ergodicity of billiards in polygons, Sb. Math. 188 (1997), 389–434.Google Scholar
Yoccoz, J. C., Interval exchange maps and translation surface, in Homogeneous Flows, Moduli Spaces and Arithmetic, Clay Mathematics Proceedings, Volume 10, pp. 1–69 (American Mathematical Society, Providence, RI, 2010).Google Scholar