1 results
The Chen–Ruan Cohomology of Weighted Projective Spaces
-
- Journal:
- Canadian Journal of Mathematics / Volume 59 / Issue 5 / 01 October 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 981-1007
- Print publication:
- 01 October 2007
-
- Article
-
- You have access
- Export citation
-
In this paper we study the Chen–Ruan cohomology ring of weighted projective spaces. Given a weighted projective space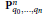
${{\mathbf{P}}^{n}}_{{{q}_{0}},\ldots ,{{q}_{n}}}$, we determine all of its twisted sectors and the corresponding degree shifting numbers. The main result of this paper is that the obstruction bundle over any 3-multisector is a direct sum of line bundles which we use to compute the orbifold cup product. Finally we compute the Chen–Ruan cohomology ring of weighted projective space 
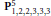$\mathbf{P}_{1,\,2,\,2,\,3,3,\,{{3}^{\centerdot }}}^{5}$.
