Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T22:09:44.581Z Has data issue: false hasContentIssue false
  • English
  • Français

The Chen–Ruan Cohomology of Weighted Projective Spaces

Published online by Cambridge University Press:  20 November 2018

Yunfeng Jiang
Yunfeng Jiang*
Affiliation:
Department of Mathematics, University of British Columbia, 1984 Mathematics Road, Vancouver, BC, V6T 1Z2 email: jiangyf@math.ubc.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we study the Chen–Ruan cohomology ring of weighted projective spaces. Given a weighted projective space 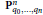${{\mathbf{P}}^{n}}_{{{q}_{0}},\ldots ,{{q}_{n}}}$, we determine all of its twisted sectors and the corresponding degree shifting numbers. The main result of this paper is that the obstruction bundle over any 3-multisector is a direct sum of line bundles which we use to compute the orbifold cup product. Finally we compute the Chen–Ruan cohomology ring of weighted projective space 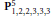$\mathbf{P}_{1,\,2,\,2,\,3,3,\,{{3}^{\centerdot }}}^{5}$.

Keywords

14N3553D45Chen–Ruan cohomologytwisted sectorstoric varietiesweighted projective spacelocalization
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 59 , Issue 5 , 01 October 2007 , pp. 981 - 1007
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Amrami, A. A., Cohomological study of weighted projective space. In: Algebraic Geometry. Lecture Notes in Pure and Applied Mathematics 193, Marcel Dekker, New York, 1997.Google Scholar
[2] Atiyah, M. and Bott, R., The moment map and equivariant cohomology. Topology 23(1984), no. 1, 1–28.Google Scholar
[3] Borisov, L., Chen, L. and Smith, G., The orbifold Chow ring of toric Deligne-Mumford stacks. J. Amer. Math. Soc. 18(2005), no.1, 193–215.Google Scholar
[4] Conrads, H., Weighted projective spaces and reflexive simplices. Manuscripta Math. 107(2002), no. 2, 215–227.Google Scholar
[5] Chen, W. and Ruan, Y., A new cohomology theory for orbifolds. Comm. Math. Phys. 248(2004), no. 1, 1–31.Google Scholar
[6] Dixon, L., Harvey, J., Vafa, C., and Witten, E., Strings on orbifolds. I. Nuclear Phys. B 261(1985), 678–686.Google Scholar
[7] Dixon, L., Harvey, J., Vafa, C., and Witten, E., Strings on orbifolds. II. Nuclear Phys. B 274(1986), 285–314.Google Scholar
[8] Cox, D. and Katz, S., Mirror Symmetry and Algebraic Geometry. Mathematical Surveys and Monographs 68, American Mathematical Society, Providence, RI, 1999.Google Scholar
[9] Fulton, W., Introduction to toric varieyies, Annals of Mathematics Studies 131, Princeton University Press, Princeton, NJ, 1993.Google Scholar
[10] Godinho, L., Blowing up symplectic orbifolds. Ann. Global Anal. Geom. 20(2001), no. 2, 117–162.Google Scholar
[11] Kawaski, T., Cohomology of twisted projective spaces and lens complexes.. Math. Ann. 206(1973), 243–248.Google Scholar
[12] Kawaski, T., The signature theorem for V-manifolds. Topology 17(1978), 75–83.Google Scholar
[13] Kobayashi, S. and Nomizu, K., Foundations of differential geometry. Vol. I, Interscience Publishers, New York, 1963.Google Scholar
[14] Oda, T., Covex Bodies and Algebraic Geometry, Ergebnisse der Mathematik und ihrer Grenzgebiete 15, Springer-Verlag, Berlin, 1988.Google Scholar
[15] Poddar, M., Orbifold Hodge numbers of Calabi-Yau hypersurfaces. Pacific J. Math. 208(2003), no. 1, 151–167.Google Scholar
[16] Park, B. D. and Poddar, M., The Chen–Ruan cohomology ring of mirror quintic, arXiv:math.AG/0210185.Google Scholar
[17] Ruan, Y., Cohomology ring of crepant resolution of orbifolds. arXiv:math.AG/0108195.Google Scholar
[18] Zaslow, E., Topological orbifold models and quantum cohomology rings. Comm. Math. Phys. 156(1993), no. 2, 301–331.Google Scholar