Let $(z_k)$ be a sequence of distinct points in the unit disc $\mathbb {D}$ without limit points there. We are looking for a function $a(z)$ analytic in $\mathbb {D}$ and such that possesses a solution having zeros precisely at the points $z_k$, and the resulting function $a(z)$ has ‘minimal’ growth. We focus on the case of non-separated sequences $(z_k)$ in terms of the pseudohyperbolic distance when the coefficient $a(z)$ is of zero order, but $\sup _{z\in {\mathbb D}}(1-|z|)^p|a(z)| = + \infty$ for any $p > 0$. We established a new estimate for the maximum modulus of $a(z)$ in terms of the functions $n_z(t)=\sum \nolimits _{|z_k-z|\le t} 1$ and $N_z(r) = \int_0^r {{(n_z(t)-1)}^ + } /t{\rm d}t.$ The estimate is sharp in some sense. The main result relies on a new interpolation theorem.

We obtain lower bounds for the growth of solutions of higher order linear differential equations, with coefficients analytic in the unit disc of the complex plane, by localising the equations via conformal maps and applying known results for the unit disc. As an example, we study equations in which the coefficients have a certain explicit exponential growth at one point on the boundary of the unit disc and consider the iterated 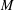$M$-order of solutions.

Let m be a measure supported on a relatively closed subset X of the unit disc. If f is a bounded function on the unit circle, let fm denote the restriction to X of the harmonic extension of f to the unit disc. We characterize those m such that the pre-adjoint of the linear map f → fm has a non-trivial kernel.