Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T22:28:17.935Z Has data issue: false hasContentIssue false
  • English
  • Français

LOCALISATION OF LINEAR DIFFERENTIAL EQUATIONS IN THE UNIT DISC BY A CONFORMAL MAP

Part of: Differential equations in the complex domain Entire and meromorphic functions, and related topics

Published online by Cambridge University Press:  15 October 2015

JUHA-MATTI HUUSKO
JUHA-MATTI HUUSKO*
Affiliation:
Department of Physics and Mathematics, University of Eastern Finland, P.O. Box 111, 80101 Joensuu, Finland email juha-matti.huusko@uef.fi
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We obtain lower bounds for the growth of solutions of higher order linear differential equations, with coefficients analytic in the unit disc of the complex plane, by localising the equations via conformal maps and applying known results for the unit disc. As an example, we study equations in which the coefficients have a certain explicit exponential growth at one point on the boundary of the unit disc and consider the iterated 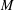$M$-order of solutions.

Keywords

complex differential equationsgrowth of solutionsunit disclocalisation

MSC classification

Primary: 34M10: Oscillation, growth of solutions
Secondary: 30D35: Distribution of values, Nevanlinna theory
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 93 , Issue 2 , April 2016 , pp. 260 - 271
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Amemiya, I. and Ozawa, M., ‘Non-existence of finite order solutions of w ′′ + e −zw ′ + Q (z)w = 0’, Hokkaido Math. J. 10 (1981), 1–17.Google Scholar
Chen, Z. X., ‘The growth of solutions of f ′′ + e −zf ′ + Q (z)f = 0, where the order (Q) = 1’, Sci. China Ser. A 45 (2002), 290–300.Google Scholar
Chen, Z. X. and Shon, K. H., ‘On the growth of solutions of a class of higher order linear differential equations’, Acta Math. Sci. Ser. B 24(1) (2004), 52–60.CrossRefGoogle Scholar
Chen, Z. X. and Shon, K. H., ‘The growth of solutions of differential equations with coefficients of small growth in the disc’, J. Math. Anal. Appl. 297 (2004), 285–304.Google Scholar
Gallardo-Gutiérrez, E. A., González, M. J., Pérez-González, F., Pommerenke, Ch. and Rättyä, J., ‘Locally univalent functions, VMOA and the Dirichlet space’, Proc. Lond. Math. Soc. (3) 106(3) (2013), 565–588.CrossRefGoogle Scholar
Gehring, F. W. and Pommerenke, Ch., ‘On the Nehari univalence criterion and quasicircles’, Comment. Math. Helv. 59(2) (1984), 226–242.Google Scholar
Gundersen, G. G., ‘On the question of whether f ′′ + e −zf ′ + B (z)f = 0 can admit a solution f̸ ≡ 0 of finite order’, Proc. Roy. Soc. Edinburgh Sect. A 102 (1986), 9–17.Google Scholar
Gundersen, G. G., ‘Finite order solutions of second order linear differential equations’, Trans. Amer. Math. Soc. 305 (1988), 415–429.Google Scholar
Hamouda, S., ‘Properties of solutions to linear differential equations with analytic coefficients in the unit disc’, Electron. J. Differential Equations 177 (2012), 1–8.Google Scholar
Hamouda, S., ‘Iterated order of solutions of linear differential equations in the unit disc’, Comput. Methods Funct. Theory 13(4) (2013), 545–555.Google Scholar
Heittokangas, J., Korhonen, R. and Rättyä, J., ‘Fast growing solutions of linear differential equations in the unit disc’, Results Math. 49 (2006), 265–278.Google Scholar
Heittokangas, J., Korhonen, R. and Rättyä, J., ‘Linear differential equations with solutions in the Dirichlet type subspace of the Hardy space’, Nagoya Math. J. 187 (2007), 91–113.Google Scholar
Kinnunen, L., ‘Linear differential equations with solution of finite iterated order’, Southeast Asian Bull. Math. 22(4) (1998), 1–8.Google Scholar