Let $p(\cdot ):\mathbb{R}^{n}\rightarrow (0,\infty )$ be a variable exponent function satisfying the globally log-Hölder continuous condition. In this paper, we obtain the boundedness of paraproduct operators $\unicode[STIX]{x1D70B}_{b}$ on variable Hardy spaces $H^{p(\cdot )}(\mathbb{R}^{n})$, where $b\in \text{BMO}(\mathbb{R}^{n})$. As an application, we show that non-convolution type Calderón–Zygmund operators $T$ are bounded on $H^{p(\cdot )}(\mathbb{R}^{n})$ if and only if $T^{\ast }1=0$, where $\frac{n}{n+\unicode[STIX]{x1D716}}<\text{ess inf}_{x\in \mathbb{R}^{n}}p\leqslant \text{ess sup}_{x\in \mathbb{R}^{n}}p\leqslant 1$ and $\unicode[STIX]{x1D716}$ is the regular exponent of kernel of $T$. Our approach relies on the discrete version of Calderón’s reproducing formula, discrete Littlewood–Paley–Stein theory, almost orthogonal estimates, and variable exponents analysis techniques. These results still hold for variable Hardy space on spaces of homogeneous type by using our methods.

Let L be a one-to-one operator of type ω in L2(ℝn), with ω∈[0, π/2), which has a bounded holomorphic functional calculus and satisfies the Davies–Gaffney estimates. Let p(·): ℝn→(0, 1] be a variable exponent function satisfying the globally log-Hölder continuous condition. In this article, the authors introduce the variable Hardy space 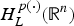$H_L^{p(\cdot )} ({\open R}^n)$ associated with L. By means of variable tent spaces, the authors establish the molecular characterization of 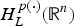$H_L^{p(\cdot )} ({\open R}^n)$. Then the authors show that the dual space of 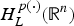$H_L^{p(\cdot )} ({\open R}^n)$ is the bounded mean oscillation (BMO)-type space 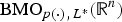${\rm BM}{\rm O}_{p(\cdot ),{\kern 1pt} L^ * }({\open R}^n)$, where L* denotes the adjoint operator of L. In particular, when L is the second-order divergence form elliptic operator with complex bounded measurable coefficients, the authors obtain the non-tangential maximal function characterization of 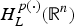$H_L^{p(\cdot )} ({\open R}^n)$ and show that the fractional integral L−α for α∈(0, (1/2)] is bounded from 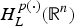$H_L^{p(\cdot )} ({\open R}^n)$ to 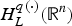$H_L^{q(\cdot )} ({\open R}^n)$ with (1/p(·))−(1/q(·))=2α/n, and the Riesz transform ∇ L−1/2 is bounded from 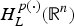$H_L^{p(\cdot )} ({\open R}^n)$ to the variable Hardy space Hp(·)(ℝn).