Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T22:42:40.517Z Has data issue: false hasContentIssue false
  • English
  • Français

Discrete Paraproduct Operators on Variable Hardy Spaces

Part of: Harmonic analysis in several variables

Published online by Cambridge University Press:  04 October 2019

Jian Tan
Jian Tan*
Affiliation:
School of Science, Nanjing University of Posts and Telecommunications, Nanjing 210023, China Email: tanjian89@126.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 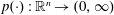$p(\cdot ):\mathbb{R}^{n}\rightarrow (0,\infty )$ be a variable exponent function satisfying the globally log-Hölder continuous condition. In this paper, we obtain the boundedness of paraproduct operators 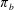$\unicode[STIX]{x1D70B}_{b}$ on variable Hardy spaces 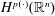$H^{p(\cdot )}(\mathbb{R}^{n})$, where 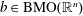$b\in \text{BMO}(\mathbb{R}^{n})$. As an application, we show that non-convolution type Calderón–Zygmund operators 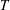$T$ are bounded on $H^{p(\cdot )}(\mathbb{R}^{n})$ if and only if 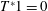$T^{\ast }1=0$, where 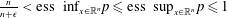$\frac{n}{n+\unicode[STIX]{x1D716}}<\text{ess inf}_{x\in \mathbb{R}^{n}}p\leqslant \text{ess sup}_{x\in \mathbb{R}^{n}}p\leqslant 1$ and $\unicode[STIX]{x1D716}$ is the regular exponent of kernel of $T$. Our approach relies on the discrete version of Calderón’s reproducing formula, discrete Littlewood–Paley–Stein theory, almost orthogonal estimates, and variable exponents analysis techniques. These results still hold for variable Hardy space on spaces of homogeneous type by using our methods.

Keywords

variable Hardy spacesingular integralparaproduct operatordiscrete Littlewood–Paley–Stein theory

MSC classification

Primary: 42B30: $H^p$-spaces
Secondary: 42B20: Singular and oscillatory integrals (Calderón-Zygmund, etc.)
Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 2 , June 2020 , pp. 304 - 317
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The project was sponsored by the Natural Science Foundation of Jiangsu Province of China (grant no. BK20180734), National Natural Science Foundation of China (No.11901309), the Natural Science Research of Jiangsu Higher Education Institutions of China (grant no. 18KJB110022), and Nanjing University of Posts and Telecommunications Science Foundation (grant nos. NY219114, NY217151).

References

Bony, J.-M., Interaction des singularités pour les équations de Klein-Gordon non linéaires. In: Goulaouic–Meyer–Schwartz seminar, 1983-1984, Exp. No. 10. École Polytech., Palaiseau.Google Scholar
Coifman, R. and Weiss, G., Analyse harmonique non-commutative sur certains espaces homogènes. (Lecture Notes in Mathematics, 242), Springer-Verlag, Berlin, 1971.10.1007/BFb0058946Google Scholar
Cruz-Uribe, D. and Fiorenza, A., Variable Lebesgue spaces. Birkhäuser/Springer Heidelberg, 2013. https://doi.org/10.1007/978-3-0348-0548-3Google Scholar
Cruz-Uribe, D., Fiorenza, A., Martell, J., and Pérez, C., The boundedness of classical operators on variable L p spaces. Ann. Acad. Sci. Fenn. Math. 31(2006), 239–264.Google Scholar
Cruz-Uribe, D., Moen, K., and Nguyen, H. V., The boundedness of multilinear Calderón-Zygmund operators on weighted and variable Hardy spaces. Publ. Mat. 63(2019), 679–713. https://doi.org/10.5565/PUBLMAT6321908Google Scholar
Cruz-Uribe, D., Moen, K., and Nguyen, H. V., A new approach to norm inequalities on weighted and variable Hardy spaces. arxiv:1902.01519Google Scholar
Cruz-Uribe, D. and Wang, L., Variable Hardy spaces. Indiana Univ. Math. J. 63(2014), 447–493. https://doi.org/10.1512/iumj.2014.63.5232Google Scholar
Deng, D.-G. and Han, Y.-S., The theory of H p spaces. Peking University Press, Beijing, 1992.Google Scholar
Deng, D.-G. and Han, Y.-S., Harmonic analysis on spaces of homogeneous type. (Lecture Notes in Mathematics, 1966), Springer-Verlag, Berlin, 2009.10.1007/978-3-540-88745-4Google Scholar
Diening, L., Harjulehto, P., Hästö, P., and Růžička, M., Lebesgue and Sobolev spaces with variable exponents. Springer, Heidelberg, 2011. https://doi.org/10.1007/978-3-642-18363-8Google Scholar
Fefferman, C. and Stein, E., H p spaces of several variables. Acta Math. 129(1972), no. 3–4, 137–193. https://doi.org/10.1007/BF02392215Google Scholar
Frazier, M. and Jawerth, B., Decomposition of Besov spaces. Indiana Univ. Math. J. 34(1985), no. 4, 777–799. https://doi.org/10.1512/iumj.1985.34.34041Google Scholar
Frazier, M. and Jawerth, B., A discrete transform and decompositions of distribution spaces. J. Funct. Anal. 93(1990), no. 1, 34–170. https://doi.org/10.1016/0022-1236(90)90137-AGoogle Scholar
Han, Y.-S., Calderón-type reproducing formula and the T b theorem. Rev. Mat. Iberoamericana 10(1994), no. 1, 51–91. https://doi.org/10.4171/RMI/145Google Scholar
Han, Y.-S., Müller, D., and Yang, D.-C., A theory of Besov and Triebel-Lizorkin spaces on metric measure spaces modeled on Carnot-Carathéodory spaces. Abstr. Appl. Anal.(2008), Art. ID 893409. https://doi.org/10.1155/2008/893409Google Scholar
Han, Y.-S., Müller, D., and Yang, D.-C., Littlewood-Paley characterizations for Hardy spaces on spaces of homogeneous type. Math. Nachr. 279(2006), no. 13-14, 1505–1537. https://doi.org/10.1002/mana.200610435Google Scholar
Han, Y.-S. and Sawyer, E., Para-accretive functions, the weak boundedness property and the Tb theorem. Rev. Mat. Iberoamericana 6(1990), 17–41. https://doi.org/10.4171/RMI/93Google Scholar
Han, Y.-S. and Sawyer, E. T., Littlewood-Paley theory on spaces of homogeneous type and the classical function spaces. Mem. Amer. Math. Soc. 110(1994), no. 530. https://doi.org/10.1090/memo/0530Google Scholar
Hung, C.-C. and Lee, M.-Y., The boundedness of Calderón-Zygmund operators by wavelet characterization. Acta Math. Sin. (Engl. Ser.) 28(2012), no. 6, 1237–1248. https://doi.org/10.1007/s10114-011-0065-0Google Scholar
Kováčik, O. and Rákosník, J., On spaces L p (x) and W k, p (x). Czechoslovak Math. J. 41(1991), 592–618.Google Scholar
Meyer, Y., Wavelets and operators. (Cambridge Studies in Advanced Mathematics, 37), Cambridge University Press, Cambridge, 1992.Google Scholar
Nakai, E. and Sawano, Y., Hardy spaces with variable exponents and generalized Campanato spaces. J. Funct. Anal. 262(2012), 3665–3748. https://doi.org/10.1016/j.jfa.2012.01.004Google Scholar
Pick, L. and Růžičkap, M., An example of a space L p (x) on which the Hardy-Littlewood maximal operator is not bounded. Expo. Math. 19(2001), 369–371. https://doi.org/10.1016/S0723-0869(01)80023-2Google Scholar
Sawano, Y., Atomic decompositions of Hardy spaces with variable exponents and its application to bounded linear operators. Integral Equations Operator Theory 77(2013), 123–148. https://doi.org/10.1007/s00020-013-2073-1Google Scholar
Stein, E. M. and Weiss, G., On the theory of harmonic functions of several variables, I. The theory of H p-spaces. Acta Math. 103(1960), 25–62. https://doi.org/10.1007/BF02546524Google Scholar
Tan, J., Atomic decomposition of variable Hardy spaces via Littlewood-Paley-Stein theory. Ann. Funct. Anal. 9(2018), no. 1, 87–100. https://doi.org/10.1215/20088752-2017-0026Google Scholar
Tan, J., Bilinear Calderón-Zygmund operators on products of variable Hardy spaces. Forum Math. 31(2019), no. 1, 187–198. https://doi.org/10.1515/forum-2018-0082Google Scholar
Tan, J., Atomic decompositions of localized Hardy spaces with variable exponents and applications. J. Geom. Anal. 29(2019), no. 1, 799–827. https://doi.org/10.1007/s12220-018-0019-1Google Scholar
Tan, J., Boundedness of maximal operator for multilinear Calderón-Zygmund operators on products of variable Hardy spaces. Kyoto J. Math.(2018), to appear.Google Scholar
Tan, J., Boundedness of multilinear fractional type operators on Hardy spaces with variable exponents, preprint.Google Scholar
Yang, D.-C., Zhuo, C.-Q., and Nakai, E., Characterizations of variable exponent Hardy spaces via Riesz transforms. Rev. Mat. Complut. 29(2016), no. 2, 245–270. https://doi.org/10.1007/s13163-016-0188-zGoogle Scholar
Zhuo, C.-Q., Sawano, Y., and Yang, D.-C., Hardy spaces with variable exponents on RD-spaces and applications. Dissertationes Math. 520(2016). https://doi.org/10.4064/dm744-9-2015Google Scholar