1 results
Geometric Perspective on Piecewise Polynomiality of Double Hurwitz Numbers
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 4 / 01 December 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 749-764
- Print publication:
- 01 December 2014
-
- Article
-
- You have access
- Export citation
-
We describe double Hurwitz numbers as intersection numbers on the moduli space of curves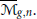
${{\overline{M}}_{g,n}}$ Using a result on the polynomiality of intersection numbers of psi classes with the Double Ramification Cycle, our formula explains the polynomiality in chambers of double Hurwitz numbers and the wall-crossing phenomenon in terms of a variation of correction terms to the 
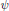$\varphi$ classes. We interpret this as suggestive evidence for polynomiality of the Double Ramification Cycle (which is only known in genera 0 and 1).
