1 results
Wb-sober spaces and the core-coherence of dcpo models
-
- Journal:
- Mathematical Structures in Computer Science / Volume 34 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 06 November 2024, pp. 529-550
-
- Article
-
- You have access
- HTML
- Export citation
-
In this paper, we introduce a new class of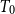
$T_0$ spaces called wb-sober spaces, which is strictly larger than the class of open well-filtered spaces. Unlike open well-filtered spaces, wb-sober spaces are defined more intuitively by requiring certain special subsets, termed wb-irreducible closed sets, to have singleton closures. We establish several key results about these spaces, including (1) every open well-filtered space is wb-sober, but not vice versa; (2) every strongly core-coherent wb-sober space is open well-filtered; (3) a space is core-compact iff its irreducible closed sets are wb-irreducible, providing a characterization of core-compactness; (4) every core-compact wb-sober space is sober, thereby generalizing the Jia-Jung problem. In addition, we investigate the core-coherence of the Xi-Zhao model. We prove that a 
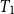$T_1$ space contains finite number of isolated points iff its Xi-Zhao model is core-coherent iff its Xi-Zhao model is strongly core-coherent. Based on this result, we then propose a general approach to constructing a non-routine open well-filtered but not well-filtered dcpo.
