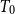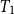1. Introduction
In domain theory, sober spaces and well-filtered spaces are two of the most important classes of topological spaces. Well-filtered spaces were introduced by Heckmann, who posed the question of whether every well-filtered Scott space of a directed complete poset is sober (Heckmann, Reference Heckmann1990,1992). This question has sparked extensive research into the relationship between sobriety and well-filteredness, as well as their respective properties (see Ho et al., Reference Ho, Goubault-Larrecq, Jung and Xi2018; Jia et al., Reference Jia, Jung and Li2016; Kou, Reference Kou2001; Liu et al., Reference Liu, Li and Wu2020; Shen et al., 2020; Wu et al., Reference Wu, Xi, Xu and Zhao2020; Xi and Lawson, Reference Xi and Lawson2017; Xi and Zhao, Reference Xi and Zhao2017; Xu, Reference Xu2021; Xu et al., Reference Xu, Shen, Xi and Zhao2020b; Zhao et al., Reference Zhao, Xi and Chen2019). A recent problem (usually called Jia-Jung problem) in this area is whether every core-compact well-filtered space is sober, as posed by Jia and Jung (Reference Jia2018, Question 2.5.19, p. 44). This question was first positively solved by Lawson et al. (Reference Lawson, Wu and Xi2020, Theorem 3.1). Some other results on this topic are as follows:
-
(i) Every first-countable well-filtered space is sober (Xu et al., Reference Xu, Shen, Xi and Zhao2020a, Theorem 4.2);
-
(ii) Every first-countable
 $\omega$
-well-filtered
$\omega$
-well-filtered
 $d$
-space is sober (Xu et al., Reference Xu, Shen, Xi and Zhao2021, Theorem 6.7);
$d$
-space is sober (Xu et al., Reference Xu, Shen, Xi and Zhao2021, Theorem 6.7); -
(iii) Every core-compact open well-filtered space is sober (Shen et al., Reference Shen, Xi, Xu and Zhao2020, Theorem 4.7).
In Section 3, we explore further aspects of the Jia-Jung problem. Specifically, consider the following implication for a topological property
![]() $ M$
:
$ M$
:
Currently, it is known that the weakest topological property satisfying this implication is the open well-filteredness. This leads us to the following question:
-
• Is there any property
 $ M$
that is weaker than open well-filteredness? To what extent can it be weakened?
$ M$
that is weaker than open well-filteredness? To what extent can it be weakened?
To address this question, it is necessary to understand the contribution of core-compactness to making a space sober. In Section 3, we introduce the notion of wb-irreducible sets, and use it to obtain a characterization of core-compactness (in the perspective of sobriety) as follows:
-
• A topological space is core-compact iff its irreducible sets are wb-irreducible.
From this, we naturally define wb-sober spaces by requiring wb-irreducible closed sets to be closures of singletons. We then prove the following results:
-
• Every open well-filtered space is wb-sober, but not vice versa. Moreover, every strongly core-coherent wb-sober space is open well-filtered.
-
• Every core-compact wb-sober space is sober, generalizing the previous result (iii).
-
• The category of wb-sober spaces with continuous mappings is not reflective in the category of
 $ T_0$
spaces.
$ T_0$
spaces.
The following section is dedicated to exploring the core-coherence of the Xi-Zhao model. A poset
![]() $P$
is called a poset model of a topological space
$P$
is called a poset model of a topological space
![]() $ X$
if
$ X$
if
![]() $X$
is homeomorphic to the set
$X$
is homeomorphic to the set
![]() $ \mathrm{Max}(P)$
of maximal elements of
$ \mathrm{Max}(P)$
of maximal elements of
![]() $P$
, equipped with the relative topology of the Scott topology of
$P$
, equipped with the relative topology of the Scott topology of
![]() $P$
. The Scott topology is one of the most significant intrinsic topologies on posets in domain theory. Generally, the Scott space of a poset is only
$P$
. The Scott topology is one of the most significant intrinsic topologies on posets in domain theory. Generally, the Scott space of a poset is only
![]() $ T_0$
. However, by considering the space of its maximal points, a richer variety of spaces can be obtained. Poset model theory has been extensively studied by various researchers and has played a crucial role in linking posets and
$ T_0$
. However, by considering the space of its maximal points, a richer variety of spaces can be obtained. Poset model theory has been extensively studied by various researchers and has played a crucial role in linking posets and
![]() $ T_1$
spaces. One related result is due to Xi and Zhao (Reference Zhao2009) and Zhao and Xi (Reference Zhao and Xi2018), who proved that every
$ T_1$
spaces. One related result is due to Xi and Zhao (Reference Zhao2009) and Zhao and Xi (Reference Zhao and Xi2018), who proved that every
![]() $ T_1$
space
$ T_1$
space
![]() $ X$
has a dcpo model, denoted by
$ X$
has a dcpo model, denoted by
![]() $\mathbf{D(X)}$
and usually called the Xi-Zhao model. Given a topological property
$\mathbf{D(X)}$
and usually called the Xi-Zhao model. Given a topological property
![]() $M$
, one can pose the following problem:
$M$
, one can pose the following problem:
-
• When a
 $ T_1$
space
$ T_1$
space
 $ X$
satisfies
$ X$
satisfies
 $ M$
, is it true that
$ M$
, is it true that
 $\mathbf{D(X)}$
equipped with the Scott topology also satisfies
$\mathbf{D(X)}$
equipped with the Scott topology also satisfies
 $M$
$M$
We say that a property
![]() $ M$
is preserved by the Xi-Zhao model if the above statement is true. It has been shown by He et al. (Reference He, Xi and Zhao2019); Xi and Zhao (Reference Xi and Zhao2017); Zhao and Xi (Reference Zhao and Xi2018) that sobriety, well-filteredness, and Choquet completeness are all preserved by the Xi-Zhao model. Recently, Chen and Li (Reference Chen and Li2022) proved that the Rudin property and weak sobriety are also preserved by the Xi-Zhao model, but core-compactness is not.
$ M$
is preserved by the Xi-Zhao model if the above statement is true. It has been shown by He et al. (Reference He, Xi and Zhao2019); Xi and Zhao (Reference Xi and Zhao2017); Zhao and Xi (Reference Zhao and Xi2018) that sobriety, well-filteredness, and Choquet completeness are all preserved by the Xi-Zhao model. Recently, Chen and Li (Reference Chen and Li2022) proved that the Rudin property and weak sobriety are also preserved by the Xi-Zhao model, but core-compactness is not.
In this paper, we address the following question:
-
• Is the core-coherent or strongly core-coherent property preserved by the Xi-Zhao model?
We provide a negative answer to this question in Section 4. Furthermore, we establish a necessary and sufficient condition for the Xi-Zhao model to be core-coherent. Specifically, we prove the following:
-
• A
 $ T_1$
space
$ T_1$
space
 $ X$
has a finite number of isolated points iff
$ X$
has a finite number of isolated points iff
 $\mathbf{D(X)}$
is strongly core-coherent iff
$\mathbf{D(X)}$
is strongly core-coherent iff
 $\mathbf{D(X)}$
is core-coherent.
$\mathbf{D(X)}$
is core-coherent.
Moreover, we show that for
![]() $T_1$
spaces, the properties of having finite isolated points and being strongly core-coherent are independent.
$T_1$
spaces, the properties of having finite isolated points and being strongly core-coherent are independent.
In the final section of the paper, we focus on developing a general approach to constructing open well-filtered (and therefore wb-sober) but not well-filtered dcpos, utilizing the Xi-Zhao model.
The concept of open well-filtered spaces, introduced by Shen et al. (Reference Shen, Xi, Xu and Zhao2020) recently, forms a larger class than that of well-filtered spaces. One notable result of open well-filtered spaces is that every core-compact open well-filtered space is sober, which strengthens the result of Jia-Jung problem Jia (Reference Jia2018) (a positive answer is originally given by Lawson et al. (Reference Lawson, Wu and Xi2020)). A recent related result is given by Chen and Li, who proved that the Xi-Zhao model of every
![]() $T_1$
space is open well-filtered (Chen and Li, Reference Chen and Li2023, Corollary 4.7).
$T_1$
space is open well-filtered (Chen and Li, Reference Chen and Li2023, Corollary 4.7).
We have observed the simplicity and validity of utilizing open well-filteredness to solve the Jia-Jung problem Shen et al. (Reference Shen, Xi, Xu and Zhao2020). However, it is important to note that the routine condition: for Scott open sets
![]() $U,V$
,
$U,V$
,
often occurs in dcpos which are not core-compact with respect to the Scott topology. Such kind of dcpos cannot fully capture the characteristic of open well-filteredness, and limit our understanding of the entire class of open well-filtered spaces. Thus, we are motivated to ask the following question:
-
• Does there exist a non-routine open well-filtered, but not well-filtered dcpo?
In Section 4.3, we provide a positive answer by proving that:
-
• The Xi-Zhao model
 $\mathbf{D(X)}$
is non-routine open well-filtered whenever
$\mathbf{D(X)}$
is non-routine open well-filtered whenever
 $X$
has at least one isolated point.
$X$
has at least one isolated point.
This result offers a method for constructing a non-routine open well-filtered, but not well-filtered dcpo.
2. Preliminary
This section is devoted to a brief review of some basic concepts and notations that will be used in the paper. For more details, see Engelking (Reference Engelking1989); Gierz et al. (Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003); Goubault-Larrecq (Reference Goubault-Larrecq2013).
Let
![]() $P$
be a poset. For a subset
$P$
be a poset. For a subset
![]() $A$
of
$A$
of
![]() $P$
, we shall adopt the following standard notations:
$P$
, we shall adopt the following standard notations:
For each
![]() $x\in X$
, we write
$x\in X$
, we write
![]() ${\mathord{\uparrow }} x={\mathord{\uparrow }}\{x\}$
and
${\mathord{\uparrow }} x={\mathord{\uparrow }}\{x\}$
and
![]() ${\mathord{\downarrow }} x={\mathord{\downarrow }} \{x\}$
. A subset
${\mathord{\downarrow }} x={\mathord{\downarrow }} \{x\}$
. A subset
![]() $A$
of
$A$
of
![]() $P$
is called a lower (resp., an upper) set if
$P$
is called a lower (resp., an upper) set if
![]() $A={\mathord{\downarrow }} A$
(resp.,
$A={\mathord{\downarrow }} A$
(resp.,
![]() $A={\mathord{\uparrow }} A$
). An element
$A={\mathord{\uparrow }} A$
). An element
![]() $x$
is maximal (resp., minimal) in
$x$
is maximal (resp., minimal) in
![]() $S\subseteq P$
, if
$S\subseteq P$
, if
![]() $S\cap{\mathord{\uparrow }} x=\{x\}$
(resp.,
$S\cap{\mathord{\uparrow }} x=\{x\}$
(resp.,
![]() $S\cap{\mathord{\downarrow }} x=\{x\}$
). The set of all maximal (resp., minimal) elements of
$S\cap{\mathord{\downarrow }} x=\{x\}$
). The set of all maximal (resp., minimal) elements of
![]() $S$
is denoted by
$S$
is denoted by
![]() $\textrm{Max}(S)$
(resp.,
$\textrm{Max}(S)$
(resp.,
![]() $\textrm{ Min}(S)$
). A nonempty subset
$\textrm{ Min}(S)$
). A nonempty subset
![]() $D$
of
$D$
of
![]() $P$
is directed (resp., filtered) if every two elements in
$P$
is directed (resp., filtered) if every two elements in
![]() $D$
have an upper (resp., lower) bound in
$D$
have an upper (resp., lower) bound in
![]() $D$
. A subset
$D$
. A subset
![]() $F$
of
$F$
of
![]() $P$
is called a filter if
$P$
is called a filter if
![]() $F$
is an upper and filtered set.
$F$
is an upper and filtered set.
![]() $P$
is called a directed complete poset, or a dcpo for short, if every directed subset of
$P$
is called a directed complete poset, or a dcpo for short, if every directed subset of
![]() $P$
has a supremum.
$P$
has a supremum.
For
![]() $x,y\in P$
,
$x,y\in P$
,
![]() $x$
is way-below
$x$
is way-below
![]() $y$
, denoted by
$y$
, denoted by
![]() $x\ll y$
, if for any directed subset
$x\ll y$
, if for any directed subset
![]() $D$
of
$D$
of
![]() $P$
for which
$P$
for which
![]() $\bigvee D$
exists,
$\bigvee D$
exists,
![]() $y\leq \bigvee D$
implies
$y\leq \bigvee D$
implies
![]() $x\leq d$
for some
$x\leq d$
for some
![]() $d\in D$
. Denote
$d\in D$
. Denote ![]()
![]() $ x=\{y\in P:x\ll y\}$
and
$ x=\{y\in P:x\ll y\}$
and ![]()
![]() $x=\{y\in P:y\ll x\}$
. A poset
$x=\{y\in P:y\ll x\}$
. A poset
![]() $P$
is continuous, if for any
$P$
is continuous, if for any
![]() $x\in P$
, the set
$x\in P$
, the set ![]()
![]() $x$
is directed and
$x$
is directed and
![]() $x= \bigvee$
$x= \bigvee$
![]()
![]() $x$
.
$x$
.
A subset
![]() $U$
of
$U$
of
![]() $P$
is Scott open if (i)
$P$
is Scott open if (i)
![]() $U=\mathord{\uparrow }U$
and (ii) for any directed subset
$U=\mathord{\uparrow }U$
and (ii) for any directed subset
![]() $D$
of
$D$
of
![]() $P$
for which
$P$
for which
![]() $\bigvee D$
exists,
$\bigvee D$
exists,
![]() $\bigvee D\in U$
implies
$\bigvee D\in U$
implies
![]() $D\cap U\neq \emptyset$
. All Scott open subsets of
$D\cap U\neq \emptyset$
. All Scott open subsets of
![]() $P$
form a topology on
$P$
form a topology on
![]() $P$
, called the Scott topology and denoted by
$P$
, called the Scott topology and denoted by
![]() $\sigma (P)$
. The space
$\sigma (P)$
. The space
![]() $\Sigma P=(P,\sigma (P))$
is called the Scott space of
$\Sigma P=(P,\sigma (P))$
is called the Scott space of
![]() $P$
.
$P$
.
Let
![]() $X$
be a
$X$
be a
![]() $T_0$
space. We use
$T_0$
space. We use
![]() $\mathcal{O}(X)$
(resp.,
$\mathcal{O}(X)$
(resp.,
![]() $\mathcal{C}(X)$
) to denote the set of all open (resp., closed) subsets of
$\mathcal{C}(X)$
) to denote the set of all open (resp., closed) subsets of
![]() $X$
,
$X$
,
![]() $\mathcal{O}^*(X)=\mathcal{O}(X)\setminus \{\emptyset \}$
, and
$\mathcal{O}^*(X)=\mathcal{O}(X)\setminus \{\emptyset \}$
, and
![]() $\mathcal{C}^*(X)=\mathcal{C}(X)\setminus \{\emptyset \}$
.
$\mathcal{C}^*(X)=\mathcal{C}(X)\setminus \{\emptyset \}$
.
A subset
![]() $A$
of
$A$
of
![]() $X$
is called saturated if
$X$
is called saturated if
![]() $A$
equals the intersection of all open sets containing it. The specialization order
$A$
equals the intersection of all open sets containing it. The specialization order
![]() $\leq$
on
$\leq$
on
![]() $X$
, is defined by
$X$
, is defined by
![]() $x\leq y$
iff
$x\leq y$
iff
![]() $x\in \textrm{cl}(\{y\})$
, where
$x\in \textrm{cl}(\{y\})$
, where
![]() $\textrm{cl}$
is the closure operator.
$\textrm{cl}$
is the closure operator.
Remark 2.1. Let
![]() $X$
be a
$X$
be a
![]() $T_0$
space.
$T_0$
space.
-
(1) A subset
 $A$
of
$A$
of
 $X$
is saturated iff
$X$
is saturated iff
 $A={\mathord{\uparrow }} A$
with respect to the specialization order. In particular,
$A={\mathord{\uparrow }} A$
with respect to the specialization order. In particular,
 ${\mathord{\uparrow }} x=\bigcap \{U:x\in U\in \mathcal{O}(X)\}$
(Gierz et al. 2003, Exercise O-5.14).
${\mathord{\uparrow }} x=\bigcap \{U:x\in U\in \mathcal{O}(X)\}$
(Gierz et al. 2003, Exercise O-5.14). -
(2) If
 $X$
is a
$X$
is a
 $T_1$
space, then for any
$T_1$
space, then for any
 $x,y\in X$
,
$x,y\in X$
,
 $x\leq y$
iff
$x\leq y$
iff
 $x=y$
(Goubault-Larrecq, Reference Goubault-Larrecq2013, Proposition 4.2.3). Therefore,
$x=y$
(Goubault-Larrecq, Reference Goubault-Larrecq2013, Proposition 4.2.3). Therefore,
 $\{x\}={\mathord{\uparrow }} x=\bigcap \{U:x\in U\in \mathcal{O}(X)\}$
.
$\{x\}={\mathord{\uparrow }} x=\bigcap \{U:x\in U\in \mathcal{O}(X)\}$
.
Definition 2.2.
Let
![]() $X$
be a
$X$
be a
![]() $T_0$
space. A subset
$T_0$
space. A subset
![]() $A$
of
$A$
of
![]() $X$
is irreducible if
$X$
is irreducible if
![]() $A\neq \emptyset$
, and for any
$A\neq \emptyset$
, and for any
![]() $U_1, U_2\in \mathcal{O}(X)$
, whenever
$U_1, U_2\in \mathcal{O}(X)$
, whenever
![]() $A\cap U_1\neq \emptyset$
and
$A\cap U_1\neq \emptyset$
and
![]() $A\cap U_2\neq \emptyset$
, it follows that
$A\cap U_2\neq \emptyset$
, it follows that
![]() $A\cap U_1\cap U_2\neq \emptyset$
. The space
$A\cap U_1\cap U_2\neq \emptyset$
. The space
![]() $X$
is called sober if for each irreducible closed set
$X$
is called sober if for each irreducible closed set
![]() $A$
, there exists a (unique) point
$A$
, there exists a (unique) point
![]() $x\in X$
such that
$x\in X$
such that
![]() $A=\textrm{cl}(\{x\})$
.
$A=\textrm{cl}(\{x\})$
.
Definition 2.3.
A
![]() $T_0$
space
$T_0$
space
![]() $X$
is called well-filtered if for any filtered family
$X$
is called well-filtered if for any filtered family
![]() $\mathcal{F}$
of nonempty compact saturated subsets of
$\mathcal{F}$
of nonempty compact saturated subsets of
![]() $X$
and
$X$
and
![]() $U\in \mathcal{O}(X)$
,
$U\in \mathcal{O}(X)$
,
![]() $\bigcap \mathcal{F}\subseteq U$
implies
$\bigcap \mathcal{F}\subseteq U$
implies
![]() $K\subseteq U$
for some
$K\subseteq U$
for some
![]() $K\in \mathcal{F}$
.
$K\in \mathcal{F}$
.
Definition 2.4 (Shen et al., Reference Shen, Xi, Xu and Zhao2020, Definition 4.1). Let
![]() $X$
be a
$X$
be a
![]() $T_0$
space.
$T_0$
space.
-
(1) A subfamily
 $\mathcal{F}$
of
$\mathcal{F}$
of
 $\mathcal{O}(X)$
is called
$\mathcal{O}(X)$
is called
 $\ll$
-filtered if for each
$\ll$
-filtered if for each
 $U_1,U_2\in \mathcal{F}$
, there is
$U_1,U_2\in \mathcal{F}$
, there is
 $U_3\in \mathcal{F}$
such that
$U_3\in \mathcal{F}$
such that
 $U_3\ll U_1$
and
$U_3\ll U_1$
and
 $U_3\ll U_2$
in
$U_3\ll U_2$
in
 $(\mathcal{O}(X),\subseteq )$
.
$(\mathcal{O}(X),\subseteq )$
. -
(2) The space
 $X$
is called open well-filtered if for each
$X$
is called open well-filtered if for each
 $\ll$
-filtered family
$\ll$
-filtered family
 $\mathcal{F}\subseteq \mathcal{O}(X)$
and
$\mathcal{F}\subseteq \mathcal{O}(X)$
and
 $U\in \mathcal{O}(X)$
,
$U\in \mathcal{O}(X)$
,
 $\bigcap \mathcal{F}\subseteq U$
implies
$\bigcap \mathcal{F}\subseteq U$
implies
 $V\subseteq U$
for some
$V\subseteq U$
for some
 $V\in \mathcal{F}$
.
$V\in \mathcal{F}$
.
Remark 2.5. Let
![]() $U,V\in \mathcal{O}(X)$
. Then,
$U,V\in \mathcal{O}(X)$
. Then,
![]() $U\not \ll V$
iff there exists a filtered subfamily
$U\not \ll V$
iff there exists a filtered subfamily
![]() $\mathcal{F}\subseteq \mathcal{C}(X)$
such that
$\mathcal{F}\subseteq \mathcal{C}(X)$
such that
![]() $V\cap \bigcap \mathcal{F}=\emptyset$
and
$V\cap \bigcap \mathcal{F}=\emptyset$
and
![]() $U\cap C\neq \emptyset$
for any
$U\cap C\neq \emptyset$
for any
![]() $C\in \mathcal{F}$
.
$C\in \mathcal{F}$
.
Let
![]() $X$
be a
$X$
be a
![]() $T_0$
space,
$T_0$
space,
![]() $A\subseteq X$
and
$A\subseteq X$
and
![]() $\emptyset \neq \mathcal{F}\subseteq \mathcal{O}(X)$
. Let
$\emptyset \neq \mathcal{F}\subseteq \mathcal{O}(X)$
. Let
In other words,
![]() $A\in m(\mathcal{F})$
iff it is a minimal (under the inclusion order) closed set that has a nonempty intersection with every member of
$A\in m(\mathcal{F})$
iff it is a minimal (under the inclusion order) closed set that has a nonempty intersection with every member of
![]() $\mathcal{F}$
.
$\mathcal{F}$
.
Lemma 2.6 (Shen et al., Reference Shen, Xi, Xu and Zhao2020, Lemma 2.4). Let
![]() $X$
be a
$X$
be a
![]() $T_0$
space and
$T_0$
space and
![]() $\mathcal{F}$
be a
$\mathcal{F}$
be a
![]() $\ll$
-filtered subfamily of
$\ll$
-filtered subfamily of
![]() $\mathcal{O}(X)$
. Then
$\mathcal{O}(X)$
. Then
![]() $m(\mathcal{F})\neq \emptyset$
(using Zorn’s Lemma), and every set in
$m(\mathcal{F})\neq \emptyset$
(using Zorn’s Lemma), and every set in
![]() $m(\mathcal{F})$
is irreducible.
$m(\mathcal{F})$
is irreducible.
Lemma 2.7 (Shen et al., Reference Shen, Xi and Zhao2022a, Theorem 3.3). Let
![]() $X$
be a
$X$
be a
![]() $T_0$
space. Then, the following statements are equivalent:
$T_0$
space. Then, the following statements are equivalent:
-
(1)
 $X$
is open well-filtered.
$X$
is open well-filtered.
-
(2) For each
 $\ll$
-filtered family
$\ll$
-filtered family
 $\mathcal{F}\subseteq \mathcal{O}(X)$
,
$\mathcal{F}\subseteq \mathcal{O}(X)$
,
 $m(\mathcal{F})\subseteq \{\textrm{cl}(\{x\}):x\in X\}$
.
$m(\mathcal{F})\subseteq \{\textrm{cl}(\{x\}):x\in X\}$
.
Definition 2.8 (Goubault-Larrecq, Reference Goubault-Larrecq2013, Definition 5.2.3). A
![]() $T_0$
space
$T_0$
space
![]() $X$
is called core-compact if
$X$
is called core-compact if
![]() $(\mathcal{O}(X),\subseteq )$
is a continuous poset.
$(\mathcal{O}(X),\subseteq )$
is a continuous poset.
Remark 2.9. The following implications hold:
-
(1) Every sober space is well-filtered (Gierz et al., Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003, Theorem II-1.21); every well-filtered space is open well-filtered (Shen et al., 2020, Theorem 4.7).
-
(2) Every core-compact open well-filtered space is sober (Shen et al., 2020, Remark 4.2).
Throughout this paper, we use
![]() $\mathbb{N}$
to denote the set of all positive integers, and let
$\mathbb{N}$
to denote the set of all positive integers, and let
![]() $\omega$
represent the first infinite ordinal. Clearly,
$\omega$
represent the first infinite ordinal. Clearly,
![]() $\omega = \{0\} \cup \mathbb{N}$
, and a set
$\omega = \{0\} \cup \mathbb{N}$
, and a set
![]() $A$
is finite iff
$A$
is finite iff
![]() $|A|\lt \omega$
.
$|A|\lt \omega$
.
3. On Wb-Sober Spaces
In this section, we introduce a new class of topological spaces, called wb-sober spaces. In contrast to the definition of open well-filtered spaces, the wb-sober spaces are defined in terms of some special sets (called wb-irreducible sets), which is more consistent with the definition of sober spaces. Another advantage is that although the wb-sobriety is weaker than open well-filteredness, but the wb-sober spaces share many important properties with the open well-filtered spaces, especially in their link to sober spaces.
Definition 3.1.
Let
![]() $X$
be a topological space.
$X$
be a topological space.
-
(1) A subset
 $A$
of
$A$
of
 $X$
is called way-below irreducible (wb-irreducible for short) if
$X$
is called way-below irreducible (wb-irreducible for short) if
 $A\neq \emptyset$
, and for any
$A\neq \emptyset$
, and for any
 $U_1,U_2\in \mathcal{O}(X)$
, whenever
$U_1,U_2\in \mathcal{O}(X)$
, whenever
 $A\cap U_1\neq \emptyset$
and
$A\cap U_1\neq \emptyset$
and
 $A\cap U_2\neq \emptyset$
, there exists
$A\cap U_2\neq \emptyset$
, there exists
 $V\in \mathcal{O}(X)$
such that
$V\in \mathcal{O}(X)$
such that
 $V\ll U_1$
,
$V\ll U_1$
,
 $V\ll U_2$
, and
$V\ll U_2$
, and
 $A\cap V\neq \emptyset$
.
$A\cap V\neq \emptyset$
. -
(2) We call
 $X$
wb-sober if it is
$X$
wb-sober if it is
 $T_0$
, and for each wb-irreducible closed set
$T_0$
, and for each wb-irreducible closed set
 $A$
, there exists a (unique)
$A$
, there exists a (unique)
 $x\in X$
such that
$x\in X$
such that
 $A=\textrm{cl}(\{x\})$
.
$A=\textrm{cl}(\{x\})$
.
Next, we provide some equivalent conditions for wb-irreducibility, which will be used in the sequel.
Lemma 3.2.
Let
![]() $X$
be a
$X$
be a
![]() $T_0$
space and
$T_0$
space and
![]() $A\subseteq X$
. Then, the following statements are equivalent:
$A\subseteq X$
. Then, the following statements are equivalent:
-
(1)
 $A$
is wb-irreducible.
$A$
is wb-irreducible.
-
(2) For any
 $U_1,U_2\in \mathcal{O}(X)$
, if
$U_1,U_2\in \mathcal{O}(X)$
, if
 $A\cap U_1\neq \emptyset$
and
$A\cap U_1\neq \emptyset$
and
 $A\cap U_2\neq \emptyset$
, then there exists
$A\cap U_2\neq \emptyset$
, then there exists
 $V\in \mathcal{O}(X)$
such that
$V\in \mathcal{O}(X)$
such that
 $V\ll U_1\cap U_2$
and
$V\ll U_1\cap U_2$
and
 $A\cap V\neq \emptyset$
.
$A\cap V\neq \emptyset$
. -
(3)
 $A$
is irreducible, and for each
$A$
is irreducible, and for each
 $U\in \mathcal{O}(X)$
, if
$U\in \mathcal{O}(X)$
, if
 $A\cap U\neq \emptyset$
, then there exists
$A\cap U\neq \emptyset$
, then there exists
 $V\in \mathcal{O}(X)$
such that
$V\in \mathcal{O}(X)$
such that
 $V\ll U$
and
$V\ll U$
and
 $A\cap V\neq \emptyset$
.
$A\cap V\neq \emptyset$
.
Proof.
(1)
![]() $\Rightarrow$
(2): Suppose
$\Rightarrow$
(2): Suppose
![]() $A$
is wb-irreducible and
$A$
is wb-irreducible and
![]() $A \cap U_1 \neq \emptyset$
and
$A \cap U_1 \neq \emptyset$
and
![]() $A \cap U_2 \neq \emptyset$
. Since
$A \cap U_2 \neq \emptyset$
. Since
![]() $A$
is wb-irreducible, there exists an open set
$A$
is wb-irreducible, there exists an open set
![]() $W$
such that
$W$
such that
![]() $W \ll U_1$
,
$W \ll U_1$
,
![]() $W \ll U_2$
, and
$W \ll U_2$
, and
![]() $A \cap W \neq \emptyset$
. Again, by the wb-irreducibility of
$A \cap W \neq \emptyset$
. Again, by the wb-irreducibility of
![]() $A$
, there exists
$A$
, there exists
![]() $V \in \mathcal{O}(X)$
such that
$V \in \mathcal{O}(X)$
such that
![]() $V \ll W$
and
$V \ll W$
and
![]() $A \cap V \neq \emptyset$
. Since
$A \cap V \neq \emptyset$
. Since
![]() $V \ll W \ll U_1$
and
$V \ll W \ll U_1$
and
![]() $V \ll W \ll U_2$
, it follows that
$V \ll W \ll U_2$
, it follows that
![]() $V \ll W \subseteq U_1 \cap U_2$
. Therefore,
$V \ll W \subseteq U_1 \cap U_2$
. Therefore,
![]() $V \ll U_1 \cap U_2$
, as desired. Hence, conclusion (2) holds.
$V \ll U_1 \cap U_2$
, as desired. Hence, conclusion (2) holds.
The implications (2)
![]() $\Rightarrow$
(3) and (3)
$\Rightarrow$
(3) and (3)
![]() $\Rightarrow$
(1) are straightforward.
$\Rightarrow$
(1) are straightforward.
The notion of wb-irreducibility helps one elucidate the core-compactness:
Proposition 3.3.
Let
![]() $X$
be a
$X$
be a
![]() $T_0$
space. Then, the following statements are equivalent:
$T_0$
space. Then, the following statements are equivalent:
-
(1)
 $X$
is core-compact.
$X$
is core-compact.
-
(2) Every irreducible subset of
 $X$
is wb-irreducible.
$X$
is wb-irreducible.
-
(3) For each
 $x\in X$
,
$x\in X$
,
 $\textrm{cl}(\{x\})$
is wb-irreducible.
$\textrm{cl}(\{x\})$
is wb-irreducible.
Proof.
(1)
![]() $\Rightarrow$
(2): Let
$\Rightarrow$
(2): Let
![]() $A$
be an irreducible set in
$A$
be an irreducible set in
![]() $X$
, and suppose
$X$
, and suppose
![]() $U\in \mathcal{O}(X)$
such that
$U\in \mathcal{O}(X)$
such that
![]() $A\cap U\neq \emptyset$
. Choose a point
$A\cap U\neq \emptyset$
. Choose a point
![]() $x\in A\cap U$
. Since
$x\in A\cap U$
. Since
![]() $X$
is core-compact, we have
$X$
is core-compact, we have
![]() $U=\bigcup \{V\in \mathcal{O}(X):V\ll U\}$
. Thus, there exists some
$U=\bigcup \{V\in \mathcal{O}(X):V\ll U\}$
. Thus, there exists some
![]() $V_0\in \mathcal{O}(X)$
such that
$V_0\in \mathcal{O}(X)$
such that
![]() $x\in V_0\ll U$
. Consequently,
$x\in V_0\ll U$
. Consequently,
![]() $x\in A\cap V_0\neq \emptyset$
. Therefore, by Lemma 3.2,
$x\in A\cap V_0\neq \emptyset$
. Therefore, by Lemma 3.2,
![]() $A$
is wb-irreducible.
$A$
is wb-irreducible.
The implications (2)
![]() $\Rightarrow$
(3) and (3)
$\Rightarrow$
(3) and (3)
![]() $\Rightarrow$
(1) are straightforward.
$\Rightarrow$
(1) are straightforward.
The following result, together with Theorem3.11, which will be presented later, generalizes Theorem 4.7 in Shen et al. (Reference Shen, Xi, Xu and Zhao2020). It is immediate from Proposition 3.3.
Theorem 3.4. A core-compact space is wb-sober iff it is sober.
To further investigate the relationship between sober spaces and wb-sober spaces, we introduce the concept of strong core-coherence. First, we review the definition of core-coherence.
Definition 3.5 (Goubault-Larrecq, Reference Goubault-Larrecq2013, Definition 5.2.18, Proposition 5.2.19). A topological space
![]() $X$
is said to be core-coherent if for any
$X$
is said to be core-coherent if for any
![]() $U_1,U_2,U\in \mathcal{O}(X)$
, whenever
$U_1,U_2,U\in \mathcal{O}(X)$
, whenever
![]() $U\ll U_1$
and
$U\ll U_1$
and
![]() $U\ll U_2$
, it holds that
$U\ll U_2$
, it holds that
![]() $U\ll U_1\cap U_2$
(or equivalently, for any
$U\ll U_1\cap U_2$
(or equivalently, for any
![]() $U_1,U_2,V_1,V_2\in \mathcal{O}(X)$
, whenever
$U_1,U_2,V_1,V_2\in \mathcal{O}(X)$
, whenever
![]() $V_1\ll U_1$
and
$V_1\ll U_1$
and
![]() $V_2\ll U_2$
, it holds that
$V_2\ll U_2$
, it holds that
![]() $V_1\cap V_2\ll U_1\cap U_2$
).
$V_1\cap V_2\ll U_1\cap U_2$
).
Definition 3.6.
A topological space
![]() $X$
is said to be strongly core-coherent if for any
$X$
is said to be strongly core-coherent if for any
![]() $U, U_1, U_2 \in \mathcal{O}(X)$
, whenever
$U, U_1, U_2 \in \mathcal{O}(X)$
, whenever
![]() $U_1 \ll U_2$
, it holds that
$U_1 \ll U_2$
, it holds that
![]() $U \cap U_1 \ll U \cap U_2$
.
$U \cap U_1 \ll U \cap U_2$
.
As the name suggests, every strongly core-coherent is core-coherent, which can be easily verified. However, the converse is not true in general, as demonstrated by the following examples.
Example 3.7.
-
(1) The set
 $\mathbb{R}$
of real numbers under the usual topology is core-coherent but not strongly core-coherent.
$\mathbb{R}$
of real numbers under the usual topology is core-coherent but not strongly core-coherent.
— It is known that locally compact
 $T_2$
spaces are core-coherent (see (Goubault-Larrecq, Reference Goubault-Larrecq2013, Fact 5.2.22 and Lemma 5.2.22)). Since
$T_2$
spaces are core-coherent (see (Goubault-Larrecq, Reference Goubault-Larrecq2013, Fact 5.2.22 and Lemma 5.2.22)). Since
 $\mathbb{R}$
is a locally compact
$\mathbb{R}$
is a locally compact
 $T_2$
space, it follows that
$T_2$
space, it follows that
 $\mathbb{R}$
is core-coherent. Additionally, note that
$\mathbb{R}$
is core-coherent. Additionally, note that
 $(0,1) \ll \mathbb{R}$
, as we can insert a compact subset, such as
$(0,1) \ll \mathbb{R}$
, as we can insert a compact subset, such as
 $[0,1]$
, between them. However,
$[0,1]$
, between them. However,
 $(0,1) \not \ll (0,1) = (0,1) \cap \mathbb{R}$
, implying that
$(0,1) \not \ll (0,1) = (0,1) \cap \mathbb{R}$
, implying that
 $\mathbb{R}$
is not strongly core-coherent.
$\mathbb{R}$
is not strongly core-coherent.
-
(2) The unit interval
 $[0,1]$
, as the subspace of
$[0,1]$
, as the subspace of
 $\mathbb{R}$
, is core-coherent but not strongly core-coherent.
$\mathbb{R}$
, is core-coherent but not strongly core-coherent.
— Using a similar argument as for
 $\mathbb{R}$
, we can conclude that
$\mathbb{R}$
, we can conclude that
 $[0,1]$
is core-coherent. Additionally, note that
$[0,1]$
is core-coherent. Additionally, note that
 $[0,1]$
is a compact space, so
$[0,1]$
is a compact space, so
 $[0,1]\ll [0,1]$
. However,
$[0,1]\ll [0,1]$
. However,
 $(0,1) \not \ll (0,1)$
, it follows that
$(0,1) \not \ll (0,1)$
, it follows that
 $[0,1]$
is not strongly core-coherent.
$[0,1]$
is not strongly core-coherent.
-
(3) Let
 $P = \mathbb{N} \cup \{a, b\}$
, where
$P = \mathbb{N} \cup \{a, b\}$
, where
 $a,b\notin \mathbb{N}$
and
$a,b\notin \mathbb{N}$
and
 $a \neq b$
. The partial order
$a \neq b$
. The partial order
 $\leq$
on
$\leq$
on
 $P$
is defined as follows:
$P$
is defined as follows:
-
(i)
 $a\leq b\leq n$
for each
$a\leq b\leq n$
for each
 $n \in \mathbb{N}$
;
$n \in \mathbb{N}$
; -
(ii)
 $m \leq n$
iff
$m \leq n$
iff
 $n \leq m$
in
$n \leq m$
in
 $\mathbb{N}$
under the usual order for each
$\mathbb{N}$
under the usual order for each
 $m, n \in \mathbb{N}$
.
$m, n \in \mathbb{N}$
.
The poset
 $P$
can be represented by Figure
1
. The space
$P$
can be represented by Figure
1
. The space
 $\Sigma P$
is a core-coherent space but not strongly core-coherent.
$\Sigma P$
is a core-coherent space but not strongly core-coherent.
— Indeed,
 $P$
is a bounded complete continuous dcpo, and posets of this kind are always core-coherent under the Scott topology (see (Goubault-Larrecq, Reference Goubault-Larrecq2013, p. 200, line 5)). Additionally, consider the open sets
$P$
is a bounded complete continuous dcpo, and posets of this kind are always core-coherent under the Scott topology (see (Goubault-Larrecq, Reference Goubault-Larrecq2013, p. 200, line 5)). Additionally, consider the open sets
 $U = \mathbb{N}$
,
$U = \mathbb{N}$
,
 $U_1 = \mathbb{N} \cup \{b\} = \uparrow b$
, and
$U_1 = \mathbb{N} \cup \{b\} = \uparrow b$
, and
 $U_2 = P = \uparrow a$
. Clearly,
$U_2 = P = \uparrow a$
. Clearly,
 $U_1 \ll U_2$
in
$U_1 \ll U_2$
in
 $\sigma (X)$
, but
$\sigma (X)$
, but
 $U \cap U_1 = \mathbb{N} \not \ll \mathbb{N} = U \cap U_2$
. Therefore,
$U \cap U_1 = \mathbb{N} \not \ll \mathbb{N} = U \cap U_2$
. Therefore,
 $\Sigma P$
is not strongly core-coherent.
$\Sigma P$
is not strongly core-coherent.
-
Proposition 3.8.
Let
![]() $X$
be a
$X$
be a
![]() $T_0$
space, and define
$T_0$
space, and define ![]()
![]() $ V=\{U\in \mathcal{O}(X):V\ll U\}$
for any
$ V=\{U\in \mathcal{O}(X):V\ll U\}$
for any
![]() $V\in \mathcal{O}(X)$
. Then, the following conditions are equivalent:
$V\in \mathcal{O}(X)$
. Then, the following conditions are equivalent:
-
(1)
 $X$
is strongly core-coherent.
$X$
is strongly core-coherent.
-
(2) For each
 $V\in \mathcal{O}(X)$
, if
$V\in \mathcal{O}(X)$
, if 
 $V\neq \emptyset$
, then
$V\neq \emptyset$
, then
 $W\ll W$
for any
$W\ll W$
for any
 $W\subseteq V$
.
$W\subseteq V$
. -
(3) For each
 $V\in \mathcal{O}(X)$
, if
$V\in \mathcal{O}(X)$
, if
 $ V\ll X$
, then
$ V\ll X$
, then
 $W\ll W$
for any
$W\ll W$
for any
 $W\subseteq V$
.
$W\subseteq V$
.
Proof.
(1)
![]() $\Rightarrow$
(2): Suppose
$\Rightarrow$
(2): Suppose ![]()
![]() $V \neq \emptyset$
and
$V \neq \emptyset$
and
![]() $W \subseteq V$
. Then, there exists
$W \subseteq V$
. Then, there exists
![]() $V_1 \in \mathcal{O}(X)$
such that
$V_1 \in \mathcal{O}(X)$
such that
![]() $V \ll V_1$
(thus,
$V \ll V_1$
(thus,
![]() $V \subseteq V_1$
). Since
$V \subseteq V_1$
). Since
![]() $X$
is strongly core-coherent, we have that
$X$
is strongly core-coherent, we have that
![]() $W = W \cap V \ll W \cap V_1 = W$
, as desired.
$W = W \cap V \ll W \cap V_1 = W$
, as desired.
(2)
![]() $\Rightarrow$
(3): It is clear.
$\Rightarrow$
(3): It is clear.
(3)
![]() $\Rightarrow$
(1): Suppose
$\Rightarrow$
(1): Suppose
![]() $U, U_1, U_2 \in \mathcal{O}(X)$
and
$U, U_1, U_2 \in \mathcal{O}(X)$
and
![]() $U_1 \ll U_2$
. From
$U_1 \ll U_2$
. From
![]() $U_1\ll U_2\subseteq X$
, it follows that
$U_1\ll U_2\subseteq X$
, it follows that
![]() $U_1\ll X$
. By condition (3), it holds that
$U_1\ll X$
. By condition (3), it holds that
![]() $U \cap U_1 \ll U \cap U_1\subseteq U \cap U_2$
, which implies that
$U \cap U_1 \ll U \cap U_1\subseteq U \cap U_2$
, which implies that
![]() $U \cap U_1 \ll U \cap U_2$
. Therefore,
$U \cap U_1 \ll U \cap U_2$
. Therefore,
![]() $X$
is strongly core-coherent.
$X$
is strongly core-coherent.
As an immediate consequence of Proposition 3.8, we have:
Corollary 3.9. The strongly core-coherent compact spaces are exactly the Noetherian spaces (i.e., every open subset of which is compact).
From the preceding discussion on strong core-coherence, it is evident that this property is generally difficult to satisfy for arbitrary topological spaces. However, an interesting result that we will establish in the next section is that Xi-Zhao models are readily strongly core-coherent.

Figure 1. The poset
![]() $P=\mathbb{N}\cup \{a,b\}$
.
$P=\mathbb{N}\cup \{a,b\}$
.
Next, we examine the relationship between open well-filtered spaces and wb-sober spaces.
Lemma 3.10.
Let
![]() $X$
be a
$X$
be a
![]() $T_0$
space and
$T_0$
space and
![]() $A\subseteq X$
, and define
$A\subseteq X$
, and define
Consider the following conditions:
-
(1) The set
 $A$
is wb-irreducible.
$A$
is wb-irreducible.
-
(2) The family
 $\mathcal{F}_A$
is a
$\mathcal{F}_A$
is a
 $\ll$
-filtered family such that
$\ll$
-filtered family such that
 $\textrm{cl}(A)\in m(\mathcal{F}_A)$
.
$\textrm{cl}(A)\in m(\mathcal{F}_A)$
. -
(3) There exists a
 $\ll$
-filtered subfamily
$\ll$
-filtered subfamily
 $\mathcal{F}$
of
$\mathcal{F}$
of
 $\mathcal{O}(X)$
such that
$\mathcal{O}(X)$
such that
 $\textrm{cl}(A)\in m(\mathcal{F})$
.
$\textrm{cl}(A)\in m(\mathcal{F})$
.
Then
![]() $(1) \Leftrightarrow (2) \Rightarrow (3)$
. Moreover, if
$(1) \Leftrightarrow (2) \Rightarrow (3)$
. Moreover, if
![]() $X$
is strongly core-coherent, then all three conditions are equivalent.
$X$
is strongly core-coherent, then all three conditions are equivalent.
Proof.
(1)
![]() $\Rightarrow$
(2): We first prove
$\Rightarrow$
(2): We first prove
![]() $\mathcal{F}_A$
is a
$\mathcal{F}_A$
is a
![]() $\ll$
-filtered family. Suppose
$\ll$
-filtered family. Suppose
![]() $U_1,U_2\in \mathcal{F}_A$
. Then,
$U_1,U_2\in \mathcal{F}_A$
. Then,
![]() $U_1\cap A\neq \emptyset$
and
$U_1\cap A\neq \emptyset$
and
![]() $U_2\cap A\neq \emptyset$
. Using the wb-irreducibility of
$U_2\cap A\neq \emptyset$
. Using the wb-irreducibility of
![]() $A$
, there is
$A$
, there is
![]() $U_3\in \mathcal{O}(X)$
such that
$U_3\in \mathcal{O}(X)$
such that
![]() $U_3\ll U_1, U_2$
and
$U_3\ll U_1, U_2$
and
![]() $A\cap U_3\neq \emptyset$
, which implies that
$A\cap U_3\neq \emptyset$
, which implies that
![]() $U_3\in \mathcal{F}_A$
. Hence,
$U_3\in \mathcal{F}_A$
. Hence,
![]() $\mathcal{F}_A$
is
$\mathcal{F}_A$
is
![]() $\ll$
-filtered.
$\ll$
-filtered.
Now we prove that
![]() $\textrm{cl}(A)\in m(\mathcal{F}_A)$
. It is clear that
$\textrm{cl}(A)\in m(\mathcal{F}_A)$
. It is clear that
![]() $\textrm{cl}(A)$
has a nonempty intersection with each element of
$\textrm{cl}(A)$
has a nonempty intersection with each element of
![]() $\mathcal{F}_A$
. Now suppose
$\mathcal{F}_A$
. Now suppose
![]() $C$
is a closed subset of
$C$
is a closed subset of
![]() $\textrm{cl}(A)$
such that
$\textrm{cl}(A)$
such that
![]() $C\cap U\neq \emptyset$
for each
$C\cap U\neq \emptyset$
for each
![]() $U\in \mathcal{F}_A$
. We need to prove
$U\in \mathcal{F}_A$
. We need to prove
![]() $C=\textrm{cl}(A)$
. This is true since if
$C=\textrm{cl}(A)$
. This is true since if
![]() $\textrm{cl}(A)\cap (X\setminus C)\neq \emptyset$
, then
$\textrm{cl}(A)\cap (X\setminus C)\neq \emptyset$
, then
![]() $X\setminus C\in \mathcal{F}_A$
, but
$X\setminus C\in \mathcal{F}_A$
, but
![]() $C\cap (X\setminus C)=\emptyset$
, which contradicts that
$C\cap (X\setminus C)=\emptyset$
, which contradicts that
![]() $C$
has a nonempty intersection with all elements of
$C$
has a nonempty intersection with all elements of
![]() $\mathcal{F}_A$
. Thus, we have that
$\mathcal{F}_A$
. Thus, we have that
![]() $\textrm{cl}(A)\in m(\mathcal{F}_A)$
.
$\textrm{cl}(A)\in m(\mathcal{F}_A)$
.
(2)
![]() $\Rightarrow$
(1): Suppose
$\Rightarrow$
(1): Suppose
![]() $U_1,U_2\in \mathcal{O}(X)$
such that
$U_1,U_2\in \mathcal{O}(X)$
such that
![]() $A\cap U_1\neq \emptyset$
and
$A\cap U_1\neq \emptyset$
and
![]() $A\cap U_2\neq \emptyset$
. Then,
$A\cap U_2\neq \emptyset$
. Then,
![]() $U_1,U_2\in \mathcal{F}_A$
and since
$U_1,U_2\in \mathcal{F}_A$
and since
![]() $\mathcal{F}_A$
is
$\mathcal{F}_A$
is
![]() $\ll$
-filtered, there exists
$\ll$
-filtered, there exists
![]() $U_3\in \mathcal{F}_A$
such that
$U_3\in \mathcal{F}_A$
such that
![]() $U_3\ll U_1$
and
$U_3\ll U_1$
and
![]() $U_3\ll U_2$
. From the definition of
$U_3\ll U_2$
. From the definition of
![]() $\mathcal{F}_A$
, it follows that
$\mathcal{F}_A$
, it follows that
![]() $A\cap U_3\neq \emptyset$
. This shows that
$A\cap U_3\neq \emptyset$
. This shows that
![]() $A$
is wb-irreducible.
$A$
is wb-irreducible.
That (2)
![]() $\Rightarrow$
(3) is trivial.
$\Rightarrow$
(3) is trivial.
Now suppose
![]() $X$
is a strongly core-coherent space. We prove:
$X$
is a strongly core-coherent space. We prove:
(3)
![]() $\Rightarrow$
(1): Let
$\Rightarrow$
(1): Let
![]() $U \in \mathcal{O}(X)$
satisfying that
$U \in \mathcal{O}(X)$
satisfying that
![]() $A \cap U \neq \emptyset$
. Since
$A \cap U \neq \emptyset$
. Since
![]() $\mathcal{F}$
is
$\mathcal{F}$
is
![]() $\ll$
-filtered, there exist
$\ll$
-filtered, there exist
![]() $W, V \in \mathcal{F}$
such that
$W, V \in \mathcal{F}$
such that
![]() $W \ll V$
. Given that
$W \ll V$
. Given that
![]() $X$
is strongly core-coherent, it follows from Proposition 3.8 that
$X$
is strongly core-coherent, it follows from Proposition 3.8 that
![]() $W \cap U \ll W \cap U\subseteq U$
, and thus
$W \cap U \ll W \cap U\subseteq U$
, and thus
![]() $W \cap U \ll U$
. Note that
$W \cap U \ll U$
. Note that
![]() $\textrm{cl}(A) \in m(\mathcal{F})$
, so
$\textrm{cl}(A) \in m(\mathcal{F})$
, so
![]() $A \cap W \neq \emptyset$
, and by Lemma 2.6,
$A \cap W \neq \emptyset$
, and by Lemma 2.6,
![]() $A$
is irreducible, implying that
$A$
is irreducible, implying that
![]() $A \cap W \cap U \neq \emptyset$
. Therefore, by Lemma 3.2,
$A \cap W \cap U \neq \emptyset$
. Therefore, by Lemma 3.2,
![]() $A$
is a wb-irreducible set.
$A$
is a wb-irreducible set.
Theorem 3.11.
-
(1) Every open well-filtered space is wb-sober, but not vice versa.
-
(2) Every strongly core-coherent wb-sober is open well-filtered.
Proof.
(1) Suppose
![]() $X$
is an open well-filtered space, and
$X$
is an open well-filtered space, and
![]() $A$
is a wb-irreducible closed subset of
$A$
is a wb-irreducible closed subset of
![]() $X$
. Then by Lemma 3.10, there exists a
$X$
. Then by Lemma 3.10, there exists a
![]() $\ll$
-filtered subfamily
$\ll$
-filtered subfamily
![]() $\mathcal{F}$
of
$\mathcal{F}$
of
![]() $\mathcal{O}(X)$
such that
$\mathcal{O}(X)$
such that
![]() $A\in m(\mathcal{F})$
. Since
$A\in m(\mathcal{F})$
. Since
![]() $X$
is open well-filtered, by Lemma 2.7 there exists
$X$
is open well-filtered, by Lemma 2.7 there exists
![]() $x\in X$
such that
$x\in X$
such that
![]() $A=\textrm{cl}(\{x\})$
. The uniqueness of
$A=\textrm{cl}(\{x\})$
. The uniqueness of
![]() $x$
is trivial since
$x$
is trivial since
![]() $X$
is
$X$
is
![]() $T_0$
. Thus,
$T_0$
. Thus,
![]() $X$
is wb-sober. The converse is not true, as demonstrated by Example 4.32 below.
$X$
is wb-sober. The converse is not true, as demonstrated by Example 4.32 below.
(2) Now assume
![]() $X$
is a strongly core-coherent wb-sober space. Suppose
$X$
is a strongly core-coherent wb-sober space. Suppose
![]() $\mathcal{F}\subseteq \mathcal{O}(X)$
is a
$\mathcal{F}\subseteq \mathcal{O}(X)$
is a
![]() $\ll$
-filtered family. Then by Lemma 3.10, each set in
$\ll$
-filtered family. Then by Lemma 3.10, each set in
![]() $m(\mathcal{F})$
is wb-irreducible closed, and thus is of the form
$m(\mathcal{F})$
is wb-irreducible closed, and thus is of the form
![]() $\textrm{cl}(\{x\})$
,
$\textrm{cl}(\{x\})$
,
![]() $x\in X$
, by the wb-sobriety of
$x\in X$
, by the wb-sobriety of
![]() $X$
. Using Lemma 2.7, we have that
$X$
. Using Lemma 2.7, we have that
![]() $X$
is open well-filtered.
$X$
is open well-filtered.
The following corollaries are trivial by Theorem3.11 and Remark 2.9.
Corollary 3.12.
Let
![]() $X$
be a strongly core-coherent
$X$
be a strongly core-coherent
![]() $T_0$
space. Then, the following statements are equivalent:
$T_0$
space. Then, the following statements are equivalent:
-
(1)
 $X$
is open well-filtered.
$X$
is open well-filtered.
-
(2) For each wb-irreducible closed set
 $A$
in
$A$
in
 $X$
, there exists a unique point
$X$
, there exists a unique point
 $x\in X$
such that
$x\in X$
such that
 $A=\textrm{cl}(\{x\})$
.
$A=\textrm{cl}(\{x\})$
.
Corollary 3.13. Let
Then, for any properties
![]() $\texttt{A},\texttt{A}'\in \mathcal{A}$
and
$\texttt{A},\texttt{A}'\in \mathcal{A}$
and
![]() $\texttt{B},\texttt{B}'\in \mathcal{B}$
, we have the following equivalence relation:
$\texttt{B},\texttt{B}'\in \mathcal{B}$
, we have the following equivalence relation:
Corollary 3.14.
Let
![]() $X$
be a core-compact space. Then, the following statements are equivalent:
$X$
be a core-compact space. Then, the following statements are equivalent:
-
(1)
 $X$
is wb-sober.
$X$
is wb-sober.
-
(2)
 $X$
is open well-filtered.
$X$
is open well-filtered.
-
(3)
 $X$
is well-filtered.
$X$
is well-filtered.
-
(4)
 $X$
is sober.
$X$
is sober.
According to the above arguments, we make a summary as follows:


Figure 2. The Johnstone’s dcpo
![]() $\mathbb{J}$
.
$\mathbb{J}$
.

Figure 3. Some properties on
![]() $\Sigma \mathbb{J}$
.
$\Sigma \mathbb{J}$
.
Example 3.15.
Let
![]() $\mathbb{J}=\mathbb{N}\times (\mathbb{N}\cup \{\infty \})$
be the Johnstone’s dcpo Johnstone (Reference Johnstone1981), which is ordered by
$\mathbb{J}=\mathbb{N}\times (\mathbb{N}\cup \{\infty \})$
be the Johnstone’s dcpo Johnstone (Reference Johnstone1981), which is ordered by
![]() $(m,n)\leq (m',n')$
iff either
$(m,n)\leq (m',n')$
iff either
![]() $m=m'$
and
$m=m'$
and
![]() $n\leq n'$
, or
$n\leq n'$
, or
![]() $n'=\infty$
and
$n'=\infty$
and
![]() $n\leq m'$
(see Figure
2
). The following result is useful:
$n\leq m'$
(see Figure
2
). The following result is useful:
-
•
 $\forall U,V\in \sigma (\mathbb{J})$
,
$\forall U,V\in \sigma (\mathbb{J})$
,
 $U\ll V$
iff
$U\ll V$
iff
 $U=\emptyset$
(see (Goubault-Larrecq, Reference Goubault-Larrecq2013, Exercise 5.2.15)).
$U=\emptyset$
(see (Goubault-Larrecq, Reference Goubault-Larrecq2013, Exercise 5.2.15)).
We have the following properties (as illustrated in Figure 3 ):
-
(i)
 $\Sigma \mathbb{J}$
is open well-filtered, and thus wb-sober by Theorem
3.11
. However, it is not well-filtered (see (Goubault-Larrecq, Reference Goubault-Larrecq2013, Exercise 8.3.9)).
$\Sigma \mathbb{J}$
is open well-filtered, and thus wb-sober by Theorem
3.11
. However, it is not well-filtered (see (Goubault-Larrecq, Reference Goubault-Larrecq2013, Exercise 8.3.9)).
-
(ii) Since

 $U=\{\emptyset \}$
for each
$U=\{\emptyset \}$
for each
 $U\in \sigma (\mathbb{J})$
, one can easily deduce that
$U\in \sigma (\mathbb{J})$
, one can easily deduce that
 $\Sigma \mathbb{J}$
is strongly core-coherent but not core-compact.
$\Sigma \mathbb{J}$
is strongly core-coherent but not core-compact.
Therefore, we deduce that
-
(1) The properties of strong core-coherence and core-compactness are parallel:
strong core-coherence
 $\not \Rightarrow$
core-compactness
$\not \Rightarrow$
core-compactness
 $\not \Rightarrow$
strong core-coherence.
$\not \Rightarrow$
strong core-coherence.
— The first non-implication can be demonstrated by Johnstone’s dcpo, using result (ii) mentioned above. For the second non-implication, refer to Example 3.7 (3), by noting that the Scott space of a continuous dcpo is always core-compact (see (Gierz et al., Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003, Theorem II-1.14.)).
-
(2) Strongly core-coherent open well-filtered spaces need not be well-filtered.
— This follows directed from the above results (i) and (ii) .
In the next part, we explore the reflectivity of the category of wb-sober spaces. We denote by
![]() $\mathbf{Top}_{\mathbf{0}}$
the category of all
$\mathbf{Top}_{\mathbf{0}}$
the category of all
![]() $T_0$
spaces and continuous mappings between them, and by Wb-sober the full subcategory of
$T_0$
spaces and continuous mappings between them, and by Wb-sober the full subcategory of
![]() $\mathbf{Top}_{\mathbf{0}}$
consisting of all wb-sober spaces.
$\mathbf{Top}_{\mathbf{0}}$
consisting of all wb-sober spaces.
Let
![]() $\mathbb{N}_{\text{cof}}$
denote the space
$\mathbb{N}_{\text{cof}}$
denote the space
![]() $\mathbb{N}$
endowed with the cofinite topology, where the nonempty open sets are the complements of finite subsets of
$\mathbb{N}$
endowed with the cofinite topology, where the nonempty open sets are the complements of finite subsets of
![]() $\mathbb{N}$
. The following lemma is useful.
$\mathbb{N}$
. The following lemma is useful.
Lemma 3.16 (Shen et al., Reference Shen, Xi and Zhao2022b, Theorem 4.3). If
![]() $\textbf{K}$
is a reflective subcategory of
$\textbf{K}$
is a reflective subcategory of
![]() $\textbf{Top}_0$
such that
$\textbf{Top}_0$
such that
![]() $\Sigma \mathbb{J}\in \textbf{K}$
, then
$\Sigma \mathbb{J}\in \textbf{K}$
, then
![]() $\mathbb{N}_{cof}\in \textbf{K}$
.
$\mathbb{N}_{cof}\in \textbf{K}$
.
It is known that every subset of
![]() $\mathbb{N}$
is compact in this topology. Additionally, one can easily show that
$\mathbb{N}$
is compact in this topology. Additionally, one can easily show that
![]() $\mathbb{N}$
itself is wb-irreducible, and it is not the closure of any singleton in
$\mathbb{N}$
itself is wb-irreducible, and it is not the closure of any singleton in
![]() $\mathbb{N}$
. Therefore, we have:
$\mathbb{N}$
. Therefore, we have:
Lemma 3.17.
![]() $\mathbb{N}_{cof}$
is not wb-sober.
$\mathbb{N}_{cof}$
is not wb-sober.
From Example 3.15 we know that
![]() $\Sigma \mathbb{J}\in \textbf{Wb-sober}$
. However, by Lemma 3.17,
$\Sigma \mathbb{J}\in \textbf{Wb-sober}$
. However, by Lemma 3.17,
![]() $\mathbb{N}_{cof}\not \in$
Wb-sober. Thus by Lemma 3.16, we obtain the following result.
$\mathbb{N}_{cof}\not \in$
Wb-sober. Thus by Lemma 3.16, we obtain the following result.
Theorem 3.18.
The category
Wb-sober
is not a reflective subcategory of
![]() $\textbf{Top}_0$
.
$\textbf{Top}_0$
.
4. The Core-Coherence of the Xi-Zhao Model
We have seen from Theorem3.11 that strong core-coherence plays a crucial role in linking wb-sobriety and open well-filteredness. The primary focus of this section is to investigate the following question:
-
• Does the Xi-Zhao model preserve the (strong) core-coherence?
We will present a negative answer to this question by constructing a counterexample in the final part. Moreover, we will provide a sufficient and necessary condition under which the Xi-Zhao model satisfies the (strong) core-coherence. Particularly, an interesting conclusion is that the Xi-Zhao dcpo is strongly core-coherent iff it is core-coherent.
4.1 On the Xi-Zhao model
In this part, we introduce some basic concepts and results of the Xi-Zhao model, which will be used in the sequel.
Let
![]() $X$
be a
$X$
be a
![]() $T_1$
space. We use
$T_1$
space. We use
![]() $\mathsf{OF}(X)$
to denote the family of all filters on
$\mathsf{OF}(X)$
to denote the family of all filters on
![]() $(\mathcal{O}^*(X),\subseteq )$
having nonempty intersections. For each
$(\mathcal{O}^*(X),\subseteq )$
having nonempty intersections. For each
![]() $A\subseteq X$
, let
$A\subseteq X$
, let
In particular, we simply write
![]() $\vec{x}$
for
$\vec{x}$
for
![]() $\vec{\{x\}}$
.
$\vec{\{x\}}$
.
Remark 4.1 (Zhao, Reference Zhao2009, Theorem 1). Let
![]() $X$
be a
$X$
be a
![]() $T_1$
space.
$T_1$
space.
-
(1)
 $\textrm{Max}(\mathsf{OF}(X))=\{\vec{x}:x\in X\}$
.
$\textrm{Max}(\mathsf{OF}(X))=\{\vec{x}:x\in X\}$
. -
(2) The compact elements in
 $\mathsf{OF}(X)$
are of the form
$\mathsf{OF}(X)$
are of the form
 $\vec{U}$
, where
$\vec{U}$
, where
 $U\in \mathcal{O}^*(X)$
.
$U\in \mathcal{O}^*(X)$
.
Lemma 4.2.
Let
![]() $X$
be a
$X$
be a
![]() $T_0$
space. Then, for any
$T_0$
space. Then, for any
![]() $x,y\in X$
,
$x,y\in X$
,
![]() $\vec{x}=\vec{y}$
if and only if
$\vec{x}=\vec{y}$
if and only if
![]() $x=y$
.
$x=y$
.
Proof.
It is straightforward since
![]() $X$
is a
$X$
is a
![]() $T_0$
space.
$T_0$
space.
Theorem 4.3 (Zhao and Xi, Reference Zhao and Xi2018, Lemma 1). For each
![]() $T_1$
space
$T_1$
space
![]() $X$
, there is a dcpo
$X$
, there is a dcpo
![]() $\mathbf{D(X)}$
such that
$\mathbf{D(X)}$
such that
![]() $X$
is homeomorphic to
$X$
is homeomorphic to
![]() $\textrm{Max}(\mathbf{D(X)})$
.
$\textrm{Max}(\mathbf{D(X)})$
.
The dcpo model
![]() $\mathbf{D(X)}$
in (Zhao and Xi, Reference Zhao and Xi2018, Lemma 1), usually called Xi-Zhao model, is constructed as follows:
$\mathbf{D(X)}$
in (Zhao and Xi, Reference Zhao and Xi2018, Lemma 1), usually called Xi-Zhao model, is constructed as follows:
and
![]() $(\mathcal{F},\vec{x})\leq (\mathcal{G},\vec{y})$
in
$(\mathcal{F},\vec{x})\leq (\mathcal{G},\vec{y})$
in
![]() $\mathbf{D(X)}$
iff either
$\mathbf{D(X)}$
iff either
![]() $x=y$
(or equivalently,
$x=y$
(or equivalently,
![]() $\vec{x}=\vec{y}$
) and
$\vec{x}=\vec{y}$
) and
![]() $\mathcal{F}\subseteq \mathcal{G}$
, or
$\mathcal{F}\subseteq \mathcal{G}$
, or
![]() $\mathcal{G}=\vec{y}$
and
$\mathcal{G}=\vec{y}$
and
![]() $\mathcal{F}\subseteq \vec{y}$
. Then,
$\mathcal{F}\subseteq \vec{y}$
. Then,
![]() $\textrm{Max}(\mathbf{D(X)})=\{(\vec{x},\vec{x}):x\in X\}$
and the mapping
$\textrm{Max}(\mathbf{D(X)})=\{(\vec{x},\vec{x}):x\in X\}$
and the mapping
![]() $h:X\longrightarrow \textrm{Max}(\mathbf{D(X)})$
, where
$h:X\longrightarrow \textrm{Max}(\mathbf{D(X)})$
, where
![]() $h(x)=(\vec{x},\vec{x})$
for each
$h(x)=(\vec{x},\vec{x})$
for each
![]() $x\in X$
, is a homeomorphism.
$x\in X$
, is a homeomorphism.
To avoid confusion, we use the notations
![]() $\mathbb{A},\mathbb{B}, \mathbb{F},\mathbb{U},\mathbb{V},\cdots$
to indicate subsets of
$\mathbb{A},\mathbb{B}, \mathbb{F},\mathbb{U},\mathbb{V},\cdots$
to indicate subsets of
![]() $\mathbf{D(X)}$
, while
$\mathbf{D(X)}$
, while
![]() $A,B, F,U,V,\cdots$
indicate subsets of
$A,B, F,U,V,\cdots$
indicate subsets of
![]() $X$
.
$X$
.
Remark 4.4. The dcpo model
![]() $\mathbf{D(X)}$
satisfies the following properties:
$\mathbf{D(X)}$
satisfies the following properties:
-
(1) For any
 $x\in X$
and
$x\in X$
and
 $U\in \mathcal{O}(X)$
, it is clear that
$U\in \mathcal{O}(X)$
, it is clear that
 $(\vec{U}, \vec{x})\in \mathbf{D(X)}$
iff
$(\vec{U}, \vec{x})\in \mathbf{D(X)}$
iff
 $x\in U$
.
$x\in U$
. -
(2) For any
 $x\in U\in \mathcal{O}(X)$
and
$x\in U\in \mathcal{O}(X)$
and
 $y\in V\in \mathcal{O}(X)$
(hence
$y\in V\in \mathcal{O}(X)$
(hence
 $(\vec{U}, \vec{x}), (\vec{V}, \vec{y}) \in \mathbf{D(X)}$
by (1)), if
$(\vec{U}, \vec{x}), (\vec{V}, \vec{y}) \in \mathbf{D(X)}$
by (1)), if
 $x \neq y$
, then
$x \neq y$
, then
 ${\mathord{\uparrow }}(\vec{U}, \vec{x}) \cap{\mathord{\uparrow }}(\vec{V}, \vec{y}) = \{(\vec{z}, \vec{z}) : z \in V \cap U\}$
.
${\mathord{\uparrow }}(\vec{U}, \vec{x}) \cap{\mathord{\uparrow }}(\vec{V}, \vec{y}) = \{(\vec{z}, \vec{z}) : z \in V \cap U\}$
.— Suppose
 $(\mathcal{F}, \vec{z}) \in{\mathord{\uparrow }}(\vec{U}, \vec{x}) \cap{\mathord{\uparrow }}(\vec{V}, \vec{y})$
, that is
$(\mathcal{F}, \vec{z}) \in{\mathord{\uparrow }}(\vec{U}, \vec{x}) \cap{\mathord{\uparrow }}(\vec{V}, \vec{y})$
, that is
 $(\vec{U}, \vec{x}) \leq (\mathcal{F}, \vec{z})$
and
$(\vec{U}, \vec{x}) \leq (\mathcal{F}, \vec{z})$
and
 $(\vec{V}, \vec{y}) \leq (\mathcal{F}, \vec{z})$
. There are three cases to consider:
$(\vec{V}, \vec{y}) \leq (\mathcal{F}, \vec{z})$
. There are three cases to consider:Case 1: Suppose
 $z = x$
. From
$z = x$
. From
 $x\neq y$
it follows that
$x\neq y$
it follows that
 $z \neq y$
. Since
$z \neq y$
. Since
 $(\vec{V}, \vec{y}) \leq (\mathcal{F}, \vec{z})$
, we have that
$(\vec{V}, \vec{y}) \leq (\mathcal{F}, \vec{z})$
, we have that
 $\mathcal{F} = \vec{z}$
and
$\mathcal{F} = \vec{z}$
and
 $z \in V$
(or equivalently,
$z \in V$
(or equivalently,
 $\vec{V} \subseteq \vec{z}$
). Note that
$\vec{V} \subseteq \vec{z}$
). Note that
 $z=x\in U$
by our assumption. Therefore,
$z=x\in U$
by our assumption. Therefore,
 $(\mathcal{F}, \vec{z}) = (\vec{z}, \vec{z})$
and
$(\mathcal{F}, \vec{z}) = (\vec{z}, \vec{z})$
and
 $z \in U \cap V$
.
$z \in U \cap V$
.Case 2: Suppose
 $z = y$
. It is similar to Case 1.
$z = y$
. It is similar to Case 1.Case 3: Suppose
 $z \neq x$
and
$z \neq x$
and
 $z \neq y$
. Since
$z \neq y$
. Since
 $z \neq y$
and
$z \neq y$
and
 $(\vec{V}, \vec{y}) \leq (\mathcal{F}, \vec{z})$
, it follows that
$(\vec{V}, \vec{y}) \leq (\mathcal{F}, \vec{z})$
, it follows that
 $\mathcal{F} = \vec{z}$
and
$\mathcal{F} = \vec{z}$
and
 $z \in V$
(or equivalently,
$z \in V$
(or equivalently,
 $\vec{V} \subseteq \vec{z}$
). Similarly, since
$\vec{V} \subseteq \vec{z}$
). Similarly, since
 $z \neq x$
and
$z \neq x$
and
 $(\vec{U}, \vec{x}) \leq (\mathcal{F}, \vec{z})$
, it follows that
$(\vec{U}, \vec{x}) \leq (\mathcal{F}, \vec{z})$
, it follows that
 $\mathcal{F} = \vec{z}$
and
$\mathcal{F} = \vec{z}$
and
 $z \in U$
. Therefore,
$z \in U$
. Therefore,
 $(\mathcal{F}, \vec{z}) = (\vec{z}, \vec{z})$
and
$(\mathcal{F}, \vec{z}) = (\vec{z}, \vec{z})$
and
 $z \in U \cap V$
.
$z \in U \cap V$
.From the above argument, we can deduce that
 ${\mathord{\uparrow }}(\vec{U}, \vec{x}) \cap{\mathord{\uparrow }}(\vec{V}, \vec{y}) \subseteq \{(\vec{z}, \vec{z}) : z \in V \cap U\}$
. The reverse inclusion is clear. Therefore, we get conclusion (2).
${\mathord{\uparrow }}(\vec{U}, \vec{x}) \cap{\mathord{\uparrow }}(\vec{V}, \vec{y}) \subseteq \{(\vec{z}, \vec{z}) : z \in V \cap U\}$
. The reverse inclusion is clear. Therefore, we get conclusion (2). -
(3) For each directed subset
 $\mathbb{D}$
of
$\mathbb{D}$
of
 $\mathbf{D(X)}$
, either there is a largest element in
$\mathbf{D(X)}$
, either there is a largest element in
 $\mathbb{D}$
, or there exists a directed family
$\mathbb{D}$
, or there exists a directed family
 $\{\mathcal{F}_i:i\in I\}\subseteq \mathsf{OF}(X)$
and
$\{\mathcal{F}_i:i\in I\}\subseteq \mathsf{OF}(X)$
and
 $x\in X$
such that
$x\in X$
such that
 $\mathbb{D}=\{(\mathcal{F}_i,\vec{x}):i\in I\}$
and
$\mathbb{D}=\{(\mathcal{F}_i,\vec{x}):i\in I\}$
and
 $\bigvee \mathbb{D}=(\bigvee _{i\in I}\mathcal{F}_i,\vec{x})$
(see (Zhao and Xi, Reference Zhao and Xi2018, Remark 2)).
$\bigvee \mathbb{D}=(\bigvee _{i\in I}\mathcal{F}_i,\vec{x})$
(see (Zhao and Xi, Reference Zhao and Xi2018, Remark 2)). -
(4) If
 $\mathbb{C}={\mathord{\downarrow }}\{(\mathcal{F}_i,\vec{x}_i):i\in I\}\subseteq \mathbf{D(X)}\setminus \textrm{Max}(\mathbf{D(X)})$
such that for any
$\mathbb{C}={\mathord{\downarrow }}\{(\mathcal{F}_i,\vec{x}_i):i\in I\}\subseteq \mathbf{D(X)}\setminus \textrm{Max}(\mathbf{D(X)})$
such that for any
 $j,k\in I$
,
$j,k\in I$
,
 $\vec{x}_j\neq \vec{x}_k$
whenever
$\vec{x}_j\neq \vec{x}_k$
whenever
 $j\neq k$
, then
$j\neq k$
, then
 $\mathbb{C}$
is a Scott closed subset of
$\mathbb{C}$
is a Scott closed subset of
 $\mathbf{D(X)}$
(see (Xi and Zhao, Reference Xi and Zhao2017, Remark 1)).
$\mathbf{D(X)}$
(see (Xi and Zhao, Reference Xi and Zhao2017, Remark 1)).
Corollary 4.5.
Let
![]() $X$
be a
$X$
be a
![]() $T_1$
space. Then, the following are equivalent:
$T_1$
space. Then, the following are equivalent:
-
(1)
 $X$
is a finite topological space.
$X$
is a finite topological space.
-
(2)
 $\mathbf{D(X)}$
is a finite dcpo.
$\mathbf{D(X)}$
is a finite dcpo.
-
(3)
 $\Sigma \mathbf{D(X)}$
is a compact space.
$\Sigma \mathbf{D(X)}$
is a compact space.
Proof.
(1)
![]() $\Rightarrow$
(2): Suppose
$\Rightarrow$
(2): Suppose
![]() $X$
is a finite set, that is
$X$
is a finite set, that is
![]() $|X|\lt \omega$
. We have that
$|X|\lt \omega$
. We have that
![]() $|\mathbf{D(X)}|\leq |\mathsf{OF}(X)|\times |X|\leq 2^{|\mathcal{O}(X)|}\times |X|\leq 2^{2^{|X|}}\times |X|\lt \omega$
. Therefore,
$|\mathbf{D(X)}|\leq |\mathsf{OF}(X)|\times |X|\leq 2^{|\mathcal{O}(X)|}\times |X|\leq 2^{2^{|X|}}\times |X|\lt \omega$
. Therefore,
![]() $\mathbf{D(X)}$
is a finite set.
$\mathbf{D(X)}$
is a finite set.
(2)
![]() $\Rightarrow$
(3): It is clear.
$\Rightarrow$
(3): It is clear.
(3)
![]() $\Rightarrow$
(1): Assume, on the contrary, there exists a countable subset
$\Rightarrow$
(1): Assume, on the contrary, there exists a countable subset
![]() $\{x_k:k\in \mathbb{N}\}\subseteq X$
, such that for any
$\{x_k:k\in \mathbb{N}\}\subseteq X$
, such that for any
![]() $k,m\in \mathbb{N}$
,
$k,m\in \mathbb{N}$
,
![]() $x_k\neq x_m$
whenever
$x_k\neq x_m$
whenever
![]() $k\neq m$
. For each
$k\neq m$
. For each
![]() $n\in \mathbb{N}$
, define
$n\in \mathbb{N}$
, define
By Remark 4.4(4),
![]() $\{\mathbb{C}_n:n\in \mathbb{N}\}$
is a filtered family of nonempty Scott closed subset of
$\{\mathbb{C}_n:n\in \mathbb{N}\}$
is a filtered family of nonempty Scott closed subset of
![]() $\mathbf{D(X)}$
, but
$\mathbf{D(X)}$
, but
![]() $\bigcap _{n\in \mathbb{N}}\mathbb{C}_n=\emptyset$
. This shows that
$\bigcap _{n\in \mathbb{N}}\mathbb{C}_n=\emptyset$
. This shows that
![]() $\Sigma \mathbf{D(X)}$
is not compact, as desired.
$\Sigma \mathbf{D(X)}$
is not compact, as desired.
Chen and Li (Reference Chen and Li2023, Corollary 4.7) recently verified the open well-filteredness of the Xi-Zhao model. Their result provides a way to construct open well-filtered dcpos, which we will explore further in the sequel. Here is the statement of the theorem:
Theorem 4.6 ((Chen and Li, Reference Chen and Li2023, Corollary 4.7)). The Xi-Zhao model of each
![]() $T_1$
space is open well-filtered (hence wb-sober) with respect to the Scott topology. Hence, every
$T_1$
space is open well-filtered (hence wb-sober) with respect to the Scott topology. Hence, every
![]() $T_1$
space has an open well-filtered dcpo model.
$T_1$
space has an open well-filtered dcpo model.
4.2 The (strong) core-coherence of
 $\mathbf{D(X)}$
$\mathbf{D(X)}$
The cofinite topological space
![]() $\mathbb{N}_{\text{cof}}$
often serves as a classic example (or sometimes a counterexample) in the context of the Xi-Zhao model. We observe that
$\mathbb{N}_{\text{cof}}$
often serves as a classic example (or sometimes a counterexample) in the context of the Xi-Zhao model. We observe that
![]() $\Sigma \mathbf{D}(\mathbb{N}_{\text{cof}})$
satisfies strong core-coherence (and hence core-coherence), with the proof relying heavily on the fact that
$\Sigma \mathbf{D}(\mathbb{N}_{\text{cof}})$
satisfies strong core-coherence (and hence core-coherence), with the proof relying heavily on the fact that
![]() $\mathbb{N}_{\text{cof}}$
has a finite number of isolated points (in this case, zero). Inspired by this observation, we aim to extend this result to general
$\mathbb{N}_{\text{cof}}$
has a finite number of isolated points (in this case, zero). Inspired by this observation, we aim to extend this result to general
![]() $T_1$
spaces with finitely many isolated points. Specifically, we prove that the Xi-Zhao model
$T_1$
spaces with finitely many isolated points. Specifically, we prove that the Xi-Zhao model
![]() $\Sigma \mathbf{D}(X)$
for such spaces is always core-coherent (and even strongly core-coherent). Notably, this conclusion also holds in reverse.
$\Sigma \mathbf{D}(X)$
for such spaces is always core-coherent (and even strongly core-coherent). Notably, this conclusion also holds in reverse.
To achieve this, we first introduce the following definition.
Definition 4.7.
Let
![]() $X$
be a
$X$
be a
![]() $T_1$
space. We define
$T_1$
space. We define
![]() $X_{\textrm{iso}}$
as the set of all isolated points in
$X_{\textrm{iso}}$
as the set of all isolated points in
![]() $X$
, that is,
$X$
, that is,
Lemma 4.8.
Let
![]() $X$
be a
$X$
be a
![]() $T_1$
space. Then, for any
$T_1$
space. Then, for any
![]() $x\in U\subseteq X_{\textrm{iso}}$
,
$x\in U\subseteq X_{\textrm{iso}}$
,
![]() $\mathbb{U}:={\mathord{\uparrow }}(\vec{U},\vec{x})$
is a Scott open subset of
$\mathbb{U}:={\mathord{\uparrow }}(\vec{U},\vec{x})$
is a Scott open subset of
![]() $\mathbf{D(X)}$
.
$\mathbf{D(X)}$
.
Proof.
First, note that
![]() $U\in \mathcal{O}(X)$
as
$U\in \mathcal{O}(X)$
as
![]() $U\subseteq X_{\textrm{iso}}$
. Clearly,
$U\subseteq X_{\textrm{iso}}$
. Clearly,
![]() $\mathbb{U}$
is an upper set. Assume
$\mathbb{U}$
is an upper set. Assume
![]() $\mathbb{D}$
is a directed subset of
$\mathbb{D}$
is a directed subset of
![]() $\mathbf{D(X)}$
such that
$\mathbf{D(X)}$
such that
![]() $\bigvee \mathbb{D}\in \mathbb{U}$
, that is
$\bigvee \mathbb{D}\in \mathbb{U}$
, that is
![]() $ (\vec{U},\vec{x})\leq \bigvee \mathbb{D}$
. By Remark 4.4(3), we assume there exists a directed family
$ (\vec{U},\vec{x})\leq \bigvee \mathbb{D}$
. By Remark 4.4(3), we assume there exists a directed family
![]() $\{\mathcal{F}_i:i\in I\}\subseteq \mathsf{OF}(X)$
and
$\{\mathcal{F}_i:i\in I\}\subseteq \mathsf{OF}(X)$
and
![]() $y\in X$
such that
$y\in X$
such that
![]() $\mathbb{D}=\{(\mathcal{F}_i,\vec{y}):i\in I\}$
and
$\mathbb{D}=\{(\mathcal{F}_i,\vec{y}):i\in I\}$
and
![]() $(\vec{U},\vec{x})\leq \bigvee \mathbb{D}=(\bigvee _{i\in I}\mathcal{F}_i,\vec{y})$
. There are two cases:
$(\vec{U},\vec{x})\leq \bigvee \mathbb{D}=(\bigvee _{i\in I}\mathcal{F}_i,\vec{y})$
. There are two cases:
(i) If
![]() $y=x$
, then
$y=x$
, then
![]() $\vec{U}\subseteq \bigvee _{i\in I}\mathcal{F}_i$
. By Remark 4.1(2) and
$\vec{U}\subseteq \bigvee _{i\in I}\mathcal{F}_i$
. By Remark 4.1(2) and
![]() $U\in \mathcal{O}(X)$
, there exists
$U\in \mathcal{O}(X)$
, there exists
![]() $i_0\in I$
such that
$i_0\in I$
such that
![]() $\vec{U}\subseteq \mathcal{F}_{i_0}$
, which implies that
$\vec{U}\subseteq \mathcal{F}_{i_0}$
, which implies that
![]() $(\vec{U},\vec{x})\leq (\mathcal{F}_{i_0},\vec{x})=(\mathcal{F}_{i_0},\vec{y})\in \mathbb{D}$
.
$(\vec{U},\vec{x})\leq (\mathcal{F}_{i_0},\vec{x})=(\mathcal{F}_{i_0},\vec{y})\in \mathbb{D}$
.
(ii) If
![]() $y\neq x$
, then
$y\neq x$
, then
![]() $\bigvee _{i\in I}\mathcal{F}_i=\vec{y}$
and
$\bigvee _{i\in I}\mathcal{F}_i=\vec{y}$
and
![]() $y\in U\subseteq X_{\textrm{iso}}$
, which implies that
$y\in U\subseteq X_{\textrm{iso}}$
, which implies that
![]() $\{y\}\in \mathcal{O}(X)$
. By Remark 4.1(2), there exists
$\{y\}\in \mathcal{O}(X)$
. By Remark 4.1(2), there exists
![]() $i_0\in I$
such that
$i_0\in I$
such that
![]() $\vec{y}=\mathcal{F}_{i_0}$
, so
$\vec{y}=\mathcal{F}_{i_0}$
, so
![]() $(\vec{U},\vec{x})\leq (\bigvee _{i\in I}\mathcal{F}_i,\vec{y})= (\vec{y},\vec{y})= (\mathcal{F}_{i_0},\vec{y})\in \mathbb{D}$
.
$(\vec{U},\vec{x})\leq (\bigvee _{i\in I}\mathcal{F}_i,\vec{y})= (\vec{y},\vec{y})= (\mathcal{F}_{i_0},\vec{y})\in \mathbb{D}$
.
All these show that
![]() $\mathbb{D}\cap \mathbb{U}\neq \emptyset$
. Therefore,
$\mathbb{D}\cap \mathbb{U}\neq \emptyset$
. Therefore,
![]() $\mathbb{U}\in \sigma (\mathbf{D(X)})$
, as desired.
$\mathbb{U}\in \sigma (\mathbf{D(X)})$
, as desired.
Lemma 4.9.
Let
![]() $X$
be a
$X$
be a
![]() $T_1$
space. Then, the following statements hold.
$T_1$
space. Then, the following statements hold.
-
(1) For each
 $x\in X$
,
$x\in X$
,
 $\{x\}\in \mathcal{O}(X)$
iff
$\{x\}\in \mathcal{O}(X)$
iff
 $\{(\vec{x},\vec{x})\}\in \sigma (\mathbf{D(X)})$
. In other words,
Therefore,
$\{(\vec{x},\vec{x})\}\in \sigma (\mathbf{D(X)})$
. In other words,
Therefore, \begin{equation*}\Sigma \mathbf {D(X)}_{\textrm {iso}}=\{(\vec {x},\vec {x}):x\in X_{\textrm {iso}}\}.\end{equation*}
\begin{equation*}\Sigma \mathbf {D(X)}_{\textrm {iso}}=\{(\vec {x},\vec {x}):x\in X_{\textrm {iso}}\}.\end{equation*}
 $|X_{\textrm{iso}}|=|\Sigma \mathbf{D(X)}_{\textrm{iso}}|$
. In particular,
$|X_{\textrm{iso}}|=|\Sigma \mathbf{D(X)}_{\textrm{iso}}|$
. In particular,
 $|X_{\textrm{iso}}|\lt \omega$
iff
$|X_{\textrm{iso}}|\lt \omega$
iff
 $|\Sigma \mathbf{D(X)}_{\textrm{iso}}|\lt \omega$
.
$|\Sigma \mathbf{D(X)}_{\textrm{iso}}|\lt \omega$
.
-
(2)
 $\Sigma \mathbf{D(X)}_{\textrm{iso}}\ll \Sigma \mathbf{D(X)}_{\textrm{iso}}$
in
$\Sigma \mathbf{D(X)}_{\textrm{iso}}\ll \Sigma \mathbf{D(X)}_{\textrm{iso}}$
in
 $\sigma (\mathbf{D(X)})$
iff
$\sigma (\mathbf{D(X)})$
iff
 $X_{\textrm{iso}}$
is finite.
$X_{\textrm{iso}}$
is finite.
Proof.
(1) Necessity: Suppose
![]() $\{x\}$
is an open subset of
$\{x\}$
is an open subset of
![]() $X$
. We need to prove
$X$
. We need to prove
![]() $\{(\vec{x},\vec{x})\}$
is a Scott open subset of
$\{(\vec{x},\vec{x})\}$
is a Scott open subset of
![]() $\mathbf{D(X)}$
. First, it is clear that
$\mathbf{D(X)}$
. First, it is clear that
![]() $\{(\vec{x},\vec{x})\}$
is an upper set, as the point
$\{(\vec{x},\vec{x})\}$
is an upper set, as the point
![]() $(\vec{x},\vec{x})$
is maximal. Assume
$(\vec{x},\vec{x})$
is maximal. Assume
![]() $\mathbb{D}$
is a directed subset of
$\mathbb{D}$
is a directed subset of
![]() $\mathbf{D(X)}$
such that
$\mathbf{D(X)}$
such that
![]() $\bigvee \mathbb{D}=(\vec{x},\vec{x})$
. By Remark 4.4(3), we may assume that
$\bigvee \mathbb{D}=(\vec{x},\vec{x})$
. By Remark 4.4(3), we may assume that
![]() $\mathbb{D}=\{(\mathcal{F}_i,\vec{y}):i\in I\}$
, where
$\mathbb{D}=\{(\mathcal{F}_i,\vec{y}):i\in I\}$
, where
![]() $\{\mathcal{F}_i:i\in I\}\subseteq \mathsf{OF}(X)$
is directed and
$\{\mathcal{F}_i:i\in I\}\subseteq \mathsf{OF}(X)$
is directed and
![]() $y\in X$
, so
$y\in X$
, so
![]() $(\bigvee _{i\in I}\mathcal{F}_i,\vec{y})=\bigvee \mathbb{D}=(\vec{x},\vec{x})$
. It follows that
$(\bigvee _{i\in I}\mathcal{F}_i,\vec{y})=\bigvee \mathbb{D}=(\vec{x},\vec{x})$
. It follows that
![]() $\vec{x}=\vec{y}$
(so
$\vec{x}=\vec{y}$
(so
![]() $x=y$
by Lemma 4.2), and
$x=y$
by Lemma 4.2), and
![]() $\bigvee _{i\in I}\mathcal{F}_i=\vec{x}$
. Note that
$\bigvee _{i\in I}\mathcal{F}_i=\vec{x}$
. Note that
![]() $\{x\}\in \mathcal{O}(X)$
, so by Remark 4.1(2), we have that
$\{x\}\in \mathcal{O}(X)$
, so by Remark 4.1(2), we have that
![]() $\vec{x}$
is compact in
$\vec{x}$
is compact in
![]() $\mathsf{OF}(X)$
, so there exists
$\mathsf{OF}(X)$
, so there exists
![]() $i_0\in I$
such that
$i_0\in I$
such that
![]() $\mathcal{F}_{i_0}=\vec{x}$
. This shows that
$\mathcal{F}_{i_0}=\vec{x}$
. This shows that
![]() $(\vec{x},\vec{x})=(\mathcal{F}_{i_0},\vec{x})=(\mathcal{F}_{i_0},\vec{y})\in \mathbb{D}$
. Therefore,
$(\vec{x},\vec{x})=(\mathcal{F}_{i_0},\vec{x})=(\mathcal{F}_{i_0},\vec{y})\in \mathbb{D}$
. Therefore,
![]() $\{(\vec{x},\vec{x})\}$
is a Scott open set.
$\{(\vec{x},\vec{x})\}$
is a Scott open set.
Sufficiency: Assume
![]() $\{(\vec{x},\vec{x})\}\in \sigma (\mathbf{D(X)})$
. By using the
$\{(\vec{x},\vec{x})\}\in \sigma (\mathbf{D(X)})$
. By using the
![]() $T_1$
separation of
$T_1$
separation of
![]() $X$
, one can verify that
$X$
, one can verify that
![]() $\{(\vec{U},\vec{x}):x\in U\in \mathcal{O}(X)\}$
is a directed subset of
$\{(\vec{U},\vec{x}):x\in U\in \mathcal{O}(X)\}$
is a directed subset of
![]() $\mathbf{D(X)}$
whose supremum equals
$\mathbf{D(X)}$
whose supremum equals
![]() $(\vec{x},\vec{x})$
. Then by using the Scott openness of
$(\vec{x},\vec{x})$
. Then by using the Scott openness of
![]() $\{(\vec{x},\vec{x})\}$
, there exists
$\{(\vec{x},\vec{x})\}$
, there exists
![]() $U_0\in \mathcal{O}(X)$
such that
$U_0\in \mathcal{O}(X)$
such that
![]() $(\vec{x},\vec{x})=(\vec{U}_0,\vec{x})$
. It follows that
$(\vec{x},\vec{x})=(\vec{U}_0,\vec{x})$
. It follows that
![]() $\vec{x}=\vec{U_0}$
, which implies that
$\vec{x}=\vec{U_0}$
, which implies that
![]() $\{x\}=\bigcap \vec{x}=\bigcap \vec{U}_0=U_0\in \mathcal{O}(X)$
by Remark 2.1. Thus,
$\{x\}=\bigcap \vec{x}=\bigcap \vec{U}_0=U_0\in \mathcal{O}(X)$
by Remark 2.1. Thus,
![]() $\{x\}\in \mathcal{O}(X)$
, as desired.
$\{x\}\in \mathcal{O}(X)$
, as desired.
(2) Suppose
![]() $\Sigma \mathbf{D(X)}_{\textrm{iso}}\ll \Sigma \mathbf{D(X)}_{\textrm{iso}}$
. By (1), the family
$\Sigma \mathbf{D(X)}_{\textrm{iso}}\ll \Sigma \mathbf{D(X)}_{\textrm{iso}}$
. By (1), the family
![]() $\{\{(\vec{x},\vec{x})\}:(\vec{x},\vec{x})\in \Sigma \mathbf{D(X)}_{\textrm{iso}}\}$
forms an open cover of
$\{\{(\vec{x},\vec{x})\}:(\vec{x},\vec{x})\in \Sigma \mathbf{D(X)}_{\textrm{iso}}\}$
forms an open cover of
![]() $\Sigma \mathbf{D(X)}_{\textrm{iso}}$
, so there exists a finite subset
$\Sigma \mathbf{D(X)}_{\textrm{iso}}$
, so there exists a finite subset
![]() $\mathbb{F}\subseteq \Sigma \mathbf{D(X)}_{\textrm{iso}}$
such that
$\mathbb{F}\subseteq \Sigma \mathbf{D(X)}_{\textrm{iso}}$
such that
![]() $\Sigma \mathbf{D(X)}_{\textrm{iso}}\subseteq \mathbb{F}$
. It follows that
$\Sigma \mathbf{D(X)}_{\textrm{iso}}\subseteq \mathbb{F}$
. It follows that
![]() $\Sigma \mathbf{D(X)}_{\textrm{iso}}=\mathbb{F}$
, so
$\Sigma \mathbf{D(X)}_{\textrm{iso}}=\mathbb{F}$
, so
![]() $\Sigma \mathbf{D(X)}_{\textrm{iso}}$
is finite. Using result (1), we have that
$\Sigma \mathbf{D(X)}_{\textrm{iso}}$
is finite. Using result (1), we have that
![]() $X_{\textrm{iso}}$
is finite. The converse is trivial.
$X_{\textrm{iso}}$
is finite. The converse is trivial.
Lemma 4.10.
Let
![]() $X$
be a
$X$
be a
![]() $T_1$
space and
$T_1$
space and
![]() $\mathbb{U}\in \sigma (\mathbf{D(X)})$
. Then, the following statements hold.
$\mathbb{U}\in \sigma (\mathbf{D(X)})$
. Then, the following statements hold.
-
(1)
 $\textrm{Max}(\mathbb{U})=\mathbb{U}\cap \textrm{Max}(\mathbf{D(X)})$
.
$\textrm{Max}(\mathbb{U})=\mathbb{U}\cap \textrm{Max}(\mathbf{D(X)})$
. -
(2) For each
 $(\mathcal{F},\vec{x})\in \mathbb{U}$
, there exists
$(\mathcal{F},\vec{x})\in \mathbb{U}$
, there exists
 $V\in \mathcal{O}(X)$
such that
$V\in \mathcal{O}(X)$
such that
 $(\mathcal{F},\vec{x})\geq (\vec{V},\vec{x})\in \mathbb{U}$
. In other words,
$(\mathcal{F},\vec{x})\geq (\vec{V},\vec{x})\in \mathbb{U}$
. In other words,
 \begin{equation*}\mathbb {U}={\mathord {\uparrow }}\{(\vec {V},\vec {x})\in \mathbb {U}:x\in V\in \mathcal {O}(X)\}.\end{equation*}
\begin{equation*}\mathbb {U}={\mathord {\uparrow }}\{(\vec {V},\vec {x})\in \mathbb {U}:x\in V\in \mathcal {O}(X)\}.\end{equation*}
-
(3) For each
 $V\in \mathcal{O}(X)$
and
$V\in \mathcal{O}(X)$
and
 $x\in X$
, if
$x\in X$
, if
 $(\vec{V},\vec{x})\in \mathbb{U}$
, then
$(\vec{V},\vec{x})\in \mathbb{U}$
, then
 $x\in V\subseteq \{y\in X:(\vec{y},\vec{y})\in \textrm{Max}(\mathbb{U})\}$
.
$x\in V\subseteq \{y\in X:(\vec{y},\vec{y})\in \textrm{Max}(\mathbb{U})\}$
. -
(4) If
 $|\textrm{Max}(\mathbb{U})|\lt \omega$
, then there is a finite subset
$|\textrm{Max}(\mathbb{U})|\lt \omega$
, then there is a finite subset
 $\mathbb{F}$
of
$\mathbb{F}$
of
 $\mathbf{D(X)}$
such that
$\mathbf{D(X)}$
such that
 $\mathbb{U}={\mathord{\uparrow }} \mathbb{F}$
.
$\mathbb{U}={\mathord{\uparrow }} \mathbb{F}$
.
Proof.
(1) It is clear since
![]() $\mathbb{U}$
is an upper set.
$\mathbb{U}$
is an upper set.
(2) Suppose
![]() $(\mathcal{F},\vec{x})\in \mathbb{U}$
. Note that
$(\mathcal{F},\vec{x})\in \mathbb{U}$
. Note that
![]() $\{(\vec{V},\vec{x}): V\in \mathcal{F}\}$
is a directed subset of
$\{(\vec{V},\vec{x}): V\in \mathcal{F}\}$
is a directed subset of
![]() $\mathbf{D(X)}$
whose supremum is
$\mathbf{D(X)}$
whose supremum is
![]() $(\mathcal{F},\vec{x})$
, and since
$(\mathcal{F},\vec{x})$
, and since
![]() $(\mathcal{F},\vec{x})\in \mathbb{U}\in \sigma (\mathbf{D(X)})$
, there is
$(\mathcal{F},\vec{x})\in \mathbb{U}\in \sigma (\mathbf{D(X)})$
, there is
![]() $V_0\in \mathcal{F}$
such that
$V_0\in \mathcal{F}$
such that
![]() $ (\vec{V}_0,\vec{x})\in \mathbb{U}$
. It follows that
$ (\vec{V}_0,\vec{x})\in \mathbb{U}$
. It follows that
![]() $(\mathcal{F},\vec{x})\geq (\vec{V}_0,\vec{x})$
, completing the proof.
$(\mathcal{F},\vec{x})\geq (\vec{V}_0,\vec{x})$
, completing the proof.
(3) Suppose
![]() $(\vec{V},\vec{x})\in \mathbb{U}$
. First, it is clear that
$(\vec{V},\vec{x})\in \mathbb{U}$
. First, it is clear that
![]() $x\in V$
, as
$x\in V$
, as
![]() $(\vec{V},\vec{x})\in \mathbf{D(X)}$
. Let
$(\vec{V},\vec{x})\in \mathbf{D(X)}$
. Let
![]() $y\in V$
. Then we have that
$y\in V$
. Then we have that
![]() $(\vec{y},\vec{y})\geq (\vec{V},\vec{x})\in \mathbb{U}={\mathord{\uparrow }}\mathbb{U}$
, which follows that
$(\vec{y},\vec{y})\geq (\vec{V},\vec{x})\in \mathbb{U}={\mathord{\uparrow }}\mathbb{U}$
, which follows that
![]() $(\vec{y},\vec{y})\in \mathbb{U}\cap \textrm{Max}(\mathbf{D(X)})=\textrm{Max}(\mathbb{U})$
. This proves (3).
$(\vec{y},\vec{y})\in \mathbb{U}\cap \textrm{Max}(\mathbf{D(X)})=\textrm{Max}(\mathbb{U})$
. This proves (3).
(4) Suppose there exists
![]() $m\in \mathbb{N}$
such that
$m\in \mathbb{N}$
such that
![]() $\textrm{Max}(\mathbb{U})=\{(\vec{x}_k,\vec{x}_k):1\leq k\leq m\}$
. Let
$\textrm{Max}(\mathbb{U})=\{(\vec{x}_k,\vec{x}_k):1\leq k\leq m\}$
. Let
![]() $\mathbb{F}:= \{(\vec{V},\vec{x})\in \mathbb{U}: x\in V\in \mathcal{O}(X)\}$
. For each
$\mathbb{F}:= \{(\vec{V},\vec{x})\in \mathbb{U}: x\in V\in \mathcal{O}(X)\}$
. For each
![]() $(\vec{V},\vec{x})\in \mathbb{F}$
, from (3) it follows that
$(\vec{V},\vec{x})\in \mathbb{F}$
, from (3) it follows that
![]() $x\in V\subseteq \{x_1,x_2,\cdots, x_m\}$
. Thus, we have that
$x\in V\subseteq \{x_1,x_2,\cdots, x_m\}$
. Thus, we have that
![]() $|\mathbb{F}|\leq 2^m\times m$
, and hence
$|\mathbb{F}|\leq 2^m\times m$
, and hence
![]() $\mathbb{F}$
is a finite set. By (2),
$\mathbb{F}$
is a finite set. By (2),
![]() $\mathbb{U}={\mathord{\uparrow }} \mathbb{F}$
, completing the proof.
$\mathbb{U}={\mathord{\uparrow }} \mathbb{F}$
, completing the proof.
Lemma 4.11.
Let
![]() $X$
be a
$X$
be a
![]() $T_1$
space and
$T_1$
space and
![]() $x\in U\in \mathcal{O}(X)$
. Then,
$x\in U\in \mathcal{O}(X)$
. Then,
![]() $U\neq \{x\}$
iff
$U\neq \{x\}$
iff
![]() $\vec{U}\neq \vec{x}$
.
$\vec{U}\neq \vec{x}$
.
Proof.
Suppose
![]() $U \neq \{x\}$
. Note that
$U \neq \{x\}$
. Note that
![]() $U$
is nonempty since
$U$
is nonempty since
![]() $x \in U$
. Then, there exists
$x \in U$
. Then, there exists
![]() $y \in U$
such that
$y \in U$
such that
![]() $y \neq x$
. Since
$y \neq x$
. Since
![]() $X$
is a
$X$
is a
![]() $T_1$
space,
$T_1$
space,
![]() $U \setminus \{y\}$
is an open set that contains
$U \setminus \{y\}$
is an open set that contains
![]() $x$
. Consequently,
$x$
. Consequently,
![]() $U \setminus \{y\} \in \vec{x}$
, and clearly
$U \setminus \{y\} \in \vec{x}$
, and clearly
![]() $U \setminus \{y\} \notin \vec{U}$
. Therefore,
$U \setminus \{y\} \notin \vec{U}$
. Therefore,
![]() $\vec{U} \neq \vec{x}$
. The converse is trivial.
$\vec{U} \neq \vec{x}$
. The converse is trivial.
Proposition 4.12.
Let
![]() $X$
be a
$X$
be a
![]() $T_1$
space and
$T_1$
space and
![]() $\mathbb{U}\in \sigma (\mathbf{D(X)})$
. If
$\mathbb{U}\in \sigma (\mathbf{D(X)})$
. If
![]() $|X_{\textrm{iso}}|\lt \omega$
, then the following statements are equivalent:
$|X_{\textrm{iso}}|\lt \omega$
, then the following statements are equivalent:
-
(1)
 $\mathbb{U}\ll \mathbf{D(X)}$
.
$\mathbb{U}\ll \mathbf{D(X)}$
. -
(2)
 $\mathbb{U}\ll \mathbb{V}$
for some
$\mathbb{U}\ll \mathbb{V}$
for some
 $\mathbb{V}\in \sigma (\mathbf{D(X)})$
.
$\mathbb{V}\in \sigma (\mathbf{D(X)})$
. -
(3)
 $\textrm{Max}(\mathbb{U})$
is a finite set.
$\textrm{Max}(\mathbb{U})$
is a finite set.
-
(4) There exists a finite subset
 $\mathbb{F}$
of
$\mathbb{F}$
of
 $\mathbf{D(X)}$
such that
$\mathbf{D(X)}$
such that
 $\mathbb{U}={\mathord{\uparrow }} \mathbb{F}$
.
$\mathbb{U}={\mathord{\uparrow }} \mathbb{F}$
.
Proof.
(1)
![]() $\Leftrightarrow$
(2): It is trivial.
$\Leftrightarrow$
(2): It is trivial.
(1)
![]() $\Rightarrow$
(3): Assume, on the contrary,
$\Rightarrow$
(3): Assume, on the contrary,
![]() $\textrm{Max}(\mathbb{U})$
is infinite. Then there exists a subset
$\textrm{Max}(\mathbb{U})$
is infinite. Then there exists a subset
![]() $\mathbb{M}:=\{(\vec{x}_k,\vec{x}_k):k\in \mathbb{N}\}$
of
$\mathbb{M}:=\{(\vec{x}_k,\vec{x}_k):k\in \mathbb{N}\}$
of
![]() $\textrm{Max}(\mathbb{U})$
such that for any
$\textrm{Max}(\mathbb{U})$
such that for any
![]() $m,n\in \mathbb{N}$
,
$m,n\in \mathbb{N}$
,
![]() $x_m\neq x_n$
whenever
$x_m\neq x_n$
whenever
![]() $m\neq n$
. Given that
$m\neq n$
. Given that
![]() $|X_{\textrm{iso}}| \lt \omega$
, we may, without loss of generality, assume that no singleton
$|X_{\textrm{iso}}| \lt \omega$
, we may, without loss of generality, assume that no singleton
![]() $\{x_k\}$
is open (i.e.,
$\{x_k\}$
is open (i.e.,
![]() $x_k\notin X_{\textrm{iso}}$
). If this were not the case, we could redefine
$x_k\notin X_{\textrm{iso}}$
). If this were not the case, we could redefine
![]() $\mathbb{M}' := \mathbb{M} \setminus \{(\vec{x}, \vec{x}) : \vec{x} \in X_{\textrm{iso}}\}$
. Since
$\mathbb{M}' := \mathbb{M} \setminus \{(\vec{x}, \vec{x}) : \vec{x} \in X_{\textrm{iso}}\}$
. Since
![]() $X_{\textrm{iso}}$
is finite,
$X_{\textrm{iso}}$
is finite,
![]() $\mathbb{M}'$
would still be infinite.
$\mathbb{M}'$
would still be infinite.
For each
![]() $k\in \mathbb{N}$
, note that
$k\in \mathbb{N}$
, note that
![]() $\{(\vec{U},\vec{x}_k):x_k\in U\in \mathcal{O}(X)\}$
is a directed subset of
$\{(\vec{U},\vec{x}_k):x_k\in U\in \mathcal{O}(X)\}$
is a directed subset of
![]() $\mathbf{D(X)}$
whose supremum is
$\mathbf{D(X)}$
whose supremum is
![]() $(\vec{x}_k,\vec{x}_k)$
. Since
$(\vec{x}_k,\vec{x}_k)$
. Since
![]() $(\vec{x}_k,\vec{x}_k)$
belongs to the Scott open set
$(\vec{x}_k,\vec{x}_k)$
belongs to the Scott open set
![]() $\mathbb{U}$
, there exists
$\mathbb{U}$
, there exists
![]() $U_{k}\in \mathcal{O}(X)$
such that
$U_{k}\in \mathcal{O}(X)$
such that
![]() $(\vec{U}_{k},\vec{x}_k)\in \mathbb{U}$
. Since
$(\vec{U}_{k},\vec{x}_k)\in \mathbb{U}$
. Since
![]() $\{x_k\}$
is not open (i.e.,
$\{x_k\}$
is not open (i.e.,
![]() $x_k\notin X_{\textrm{iso}}$
), it holds that
$x_k\notin X_{\textrm{iso}}$
), it holds that
![]() $U_k\neq \{x_k\}$
, and from Lemma 4.11 it follows that
$U_k\neq \{x_k\}$
, and from Lemma 4.11 it follows that
![]() $\vec{U}_{k}\neq \vec{x}_k$
, that is,
$\vec{U}_{k}\neq \vec{x}_k$
, that is,
![]() $(\vec{U}_{k},\vec{x}_k)\in \mathbf{D(X)}\setminus \textrm{Max}(\mathbf{D(X)})$
. Therefore,
$(\vec{U}_{k},\vec{x}_k)\in \mathbf{D(X)}\setminus \textrm{Max}(\mathbf{D(X)})$
. Therefore,
![]() $\{(\vec{U}_{k},\vec{x}_k):k\in \mathbb{N}\}\subseteq \mathbf{D(X)}\setminus \textrm{Max}(\mathbf{D(X)})$
. For each
$\{(\vec{U}_{k},\vec{x}_k):k\in \mathbb{N}\}\subseteq \mathbf{D(X)}\setminus \textrm{Max}(\mathbf{D(X)})$
. For each
![]() $n\in \mathbb{N}$
, define
$n\in \mathbb{N}$
, define
By Remark 4.4(4),
![]() $\{\mathbb{C}_n:n\in \mathbb{N}\}$
is a filtered family of Scott closed subset of
$\{\mathbb{C}_n:n\in \mathbb{N}\}$
is a filtered family of Scott closed subset of
![]() $\mathbf{D(X)}$
. It holds that
$\mathbf{D(X)}$
. It holds that
![]() $\bigcap _{n\in \mathbb{N}}\mathbb{C}_n=\emptyset$
, but
$\bigcap _{n\in \mathbb{N}}\mathbb{C}_n=\emptyset$
, but
![]() $(\vec{U}_n,\vec{x}_n)\in \mathbb{C}_n\cap \mathbb{U}\neq \emptyset$
, which implies that
$(\vec{U}_n,\vec{x}_n)\in \mathbb{C}_n\cap \mathbb{U}\neq \emptyset$
, which implies that
![]() $\mathbb{U}\not \ll \mathbf{D(X)}$
. Therefore, the conclusion holds.
$\mathbb{U}\not \ll \mathbf{D(X)}$
. Therefore, the conclusion holds.
(3)
![]() $\Rightarrow$
(4): It follows immediately from Lemma 4.10(4).
$\Rightarrow$
(4): It follows immediately from Lemma 4.10(4).
(4)
![]() $\Rightarrow$
(1): It is straightforward.
$\Rightarrow$
(1): It is straightforward.
Theorem 4.13.
Let
![]() $X$
be a
$X$
be a
![]() $T_1$
space. Then, the following conditions are equivalent:
$T_1$
space. Then, the following conditions are equivalent:
-
(1)
 $X_{\textrm{iso}}$
is a finite set.
$X_{\textrm{iso}}$
is a finite set.
-
(2)
 $\Sigma \mathbf{D(X)}$
is a strongly core-coherent space.
$\Sigma \mathbf{D(X)}$
is a strongly core-coherent space.
-
(3)
 $\Sigma \mathbf{D(X)}$
is a core-coherent space.
$\Sigma \mathbf{D(X)}$
is a core-coherent space.
Proof.
(1)
![]() $\Rightarrow$
(2): Suppose
$\Rightarrow$
(2): Suppose
![]() $\mathbb{U}_1,\mathbb{U}_2,\mathbb{V}\in \sigma (\mathbf{D(X)})$
such that
$\mathbb{U}_1,\mathbb{U}_2,\mathbb{V}\in \sigma (\mathbf{D(X)})$
such that
![]() $\mathbb{U}_1\ll \mathbb{U}_2$
. Then,
$\mathbb{U}_1\ll \mathbb{U}_2$
. Then,
![]() $\mathbb{V}\cap \mathbb{U}_1\subseteq \mathbb{U}_1\ll \mathbb{U}_2\subseteq \mathbf{D(X)}$
, which implies that
$\mathbb{V}\cap \mathbb{U}_1\subseteq \mathbb{U}_1\ll \mathbb{U}_2\subseteq \mathbf{D(X)}$
, which implies that
![]() $\mathbb{V}\cap \mathbb{U}_1\ll \mathbf{D(X)}$
. By Proposition 4.12, there exists a finite subset
$\mathbb{V}\cap \mathbb{U}_1\ll \mathbf{D(X)}$
. By Proposition 4.12, there exists a finite subset
![]() $\mathbb{F}$
of
$\mathbb{F}$
of
![]() $\mathbf{D(X)}$
such that
$\mathbf{D(X)}$
such that
![]() $\mathbb{V}\cap \mathbb{U}_1={\mathord{\uparrow }} \mathbb{F}$
. Since
$\mathbb{V}\cap \mathbb{U}_1={\mathord{\uparrow }} \mathbb{F}$
. Since
![]() $\mathbb{V}\cap \mathbb{U}_1={\mathord{\uparrow }} \mathbb{F}\subseteq \mathbb{V}\cap \mathbb{U}_2$
, it holds that
$\mathbb{V}\cap \mathbb{U}_1={\mathord{\uparrow }} \mathbb{F}\subseteq \mathbb{V}\cap \mathbb{U}_2$
, it holds that
![]() $\mathbb{V}\cap \mathbb{U}_1\ll \mathbb{V}\cap \mathbb{U}_2$
. This shows that
$\mathbb{V}\cap \mathbb{U}_1\ll \mathbb{V}\cap \mathbb{U}_2$
. This shows that
![]() $\Sigma \mathbf{D(X)}$
is strongly core-coherent.
$\Sigma \mathbf{D(X)}$
is strongly core-coherent.
(2)
![]() $\Rightarrow$
(3): It is clear.
$\Rightarrow$
(3): It is clear.
(3)
![]() $\Rightarrow$
(1): If
$\Rightarrow$
(1): If
![]() $|X_{\textrm{iso}}|\leq 2$
, then the conclusion holds. Assume
$|X_{\textrm{iso}}|\leq 2$
, then the conclusion holds. Assume
![]() $|X_{\textrm{iso}}|\geq 2$
, and then we can choose
$|X_{\textrm{iso}}|\geq 2$
, and then we can choose
![]() $x,y\in X_{\textrm{iso}}$
with
$x,y\in X_{\textrm{iso}}$
with
![]() $x\neq y$
. Note that
$x\neq y$
. Note that
![]() $X_{\textrm{iso}}\in \mathcal{O}(X)$
, and then by Lemma 4.8,
$X_{\textrm{iso}}\in \mathcal{O}(X)$
, and then by Lemma 4.8,
![]() $\mathbb{U}:={\mathord{\uparrow }} (\vec{X}_{\textrm{iso}},\vec{x})\in \sigma (\mathbf{D(X)})$
and
$\mathbb{U}:={\mathord{\uparrow }} (\vec{X}_{\textrm{iso}},\vec{x})\in \sigma (\mathbf{D(X)})$
and
![]() $\mathbb{V}:={\mathord{\uparrow }} (\vec{X}_{\textrm{iso}},\vec{y})\in \sigma (\mathbf{D(X)})$
. It is clear that both
$\mathbb{V}:={\mathord{\uparrow }} (\vec{X}_{\textrm{iso}},\vec{y})\in \sigma (\mathbf{D(X)})$
. It is clear that both
![]() $\mathbb{U}$
and
$\mathbb{U}$
and
![]() $\mathbb{V}$
are compact saturated sets in
$\mathbb{V}$
are compact saturated sets in
![]() $\sigma (\mathbf{D(X)})$
, so
$\sigma (\mathbf{D(X)})$
, so
![]() $\mathbb{U}\ll \mathbb{U}$
and
$\mathbb{U}\ll \mathbb{U}$
and
![]() $\mathbb{V}\ll \mathbb{V}$
in
$\mathbb{V}\ll \mathbb{V}$
in
![]() $\sigma (\mathbf{D(X)})$
. Since
$\sigma (\mathbf{D(X)})$
. Since
![]() $\Sigma \mathbf{D(X)}$
is core-coherent, by Remark 4.4(2) we have that
$\Sigma \mathbf{D(X)}$
is core-coherent, by Remark 4.4(2) we have that
By Lemma 4.9(2),
![]() $X_{\textrm{iso}}$
is a finite set, completing the proof.
$X_{\textrm{iso}}$
is a finite set, completing the proof.
The following corollary is clear by Lemma 4.9, Theorems4.6, 3.11 and 4.13.
Corollary 4.14.
Let
![]() $X$
be a
$X$
be a
![]() $T_1$
space. Then, the following statements are equivalent:
$T_1$
space. Then, the following statements are equivalent:
-
(1)
 $X_{\textrm{iso}}$
is a finite set.
$X_{\textrm{iso}}$
is a finite set.
-
(2)
 $\Sigma \mathbf{D(X)}_{\textrm{iso}}$
is a finite set.
$\Sigma \mathbf{D(X)}_{\textrm{iso}}$
is a finite set.
-
(3)
 $\Sigma \mathbf{D(X)}$
is a core-coherent space.
$\Sigma \mathbf{D(X)}$
is a core-coherent space.
-
(4)
 $\Sigma \mathbf{D(X)}$
is a strongly core-coherent space.
$\Sigma \mathbf{D(X)}$
is a strongly core-coherent space.
-
(5)
 $\Sigma \mathbf{D(X)}$
is a core-coherent open well-filtered space.
$\Sigma \mathbf{D(X)}$
is a core-coherent open well-filtered space.
-
(6)
 $\Sigma \mathbf{D(X)}$
is a strongly core-coherent open well-filtered space.
$\Sigma \mathbf{D(X)}$
is a strongly core-coherent open well-filtered space.
-
(7)
 $\Sigma \mathbf{D(X)}$
is a core-coherent wb-sober space.
$\Sigma \mathbf{D(X)}$
is a core-coherent wb-sober space.
-
(8)
 $\Sigma \mathbf{D(X)}$
is a strongly core-coherent wb-sober space.
$\Sigma \mathbf{D(X)}$
is a strongly core-coherent wb-sober space.
By Theorem4.6 and Corollary 4.14, the following result is clear.
Theorem 4.15.
Every
![]() $T_1$
space having finite number of isolated points has a (strongly) core-coherent open well-filtered dcpo model.
$T_1$
space having finite number of isolated points has a (strongly) core-coherent open well-filtered dcpo model.
Considering that
![]() $|(\mathbb{N}_{cof})_{\textrm{iso}}|=0\lt \omega$
, the following result holds as a direct application of Theorem4.13.
$|(\mathbb{N}_{cof})_{\textrm{iso}}|=0\lt \omega$
, the following result holds as a direct application of Theorem4.13.
Corollary 4.16.
The Scott space
![]() $\Sigma \mathbf D(\mathbb{N}_{cof})$
is (strongly) core-coherent and open well-filtered.
$\Sigma \mathbf D(\mathbb{N}_{cof})$
is (strongly) core-coherent and open well-filtered.
4.3 A non-routine open well-filtered dcpo
Definition 4.17.
A
![]() $T_0$
space
$T_0$
space
![]() $X$
is said to be routine (with respect to the way-below relation
$X$
is said to be routine (with respect to the way-below relation
![]() $\ll$
on
$\ll$
on
![]() $\mathcal{O}(X)$
) if for any
$\mathcal{O}(X)$
) if for any
![]() $U,V\in \mathcal{O}(X)$
, whenever
$U,V\in \mathcal{O}(X)$
, whenever
![]() $U\ll V$
,
$U\ll V$
,
![]() $U=\emptyset$
.
$U=\emptyset$
.
Remark 4.18.
-
(1) It is trivial to verify that every routine space is strongly core-coherent (thus core-coherent) and open well-filtered:
 \begin{equation*} \text {open well-filtered \ }\,\,\,\Leftarrow \,\,\,\text {routine}\,\,\,\Rightarrow \text { \ strongly core-compact}. \end{equation*}
\begin{equation*} \text {open well-filtered \ }\,\,\,\Leftarrow \,\,\,\text {routine}\,\,\,\Rightarrow \text { \ strongly core-compact}. \end{equation*}
-
(2) The Scott space of the Johnstone’s dcpo is routine, as shown in Example 3.15.
Theorem 4.19.
Let
![]() $X$
be a
$X$
be a
![]() $T_1$
space. Then, the following statements are equivalent:
$T_1$
space. Then, the following statements are equivalent:
-
(1)
 $X_{\textrm{iso}}=\emptyset$
.
$X_{\textrm{iso}}=\emptyset$
. -
(2)
 $\Sigma \mathbf{D(X)}$
is a routine space.
$\Sigma \mathbf{D(X)}$
is a routine space.
Proof.
(1)
![]() $\Rightarrow$
(2): Assume, on the contrary, that
$\Rightarrow$
(2): Assume, on the contrary, that
![]() $\Sigma \mathbf{D(X)}$
is non-routine. Then, there exist
$\Sigma \mathbf{D(X)}$
is non-routine. Then, there exist
![]() $\mathbb{U},\mathbb{V}\in \sigma (\mathbf{D(X)})$
such that
$\mathbb{U},\mathbb{V}\in \sigma (\mathbf{D(X)})$
such that
![]() $\emptyset \neq \mathbb{U}\ll \mathbb{V}$
. Then, it is clear that
$\emptyset \neq \mathbb{U}\ll \mathbb{V}$
. Then, it is clear that
![]() $\mathbb{U}\ll \mathbf{D(X)}$
. By Proposition 4.12,
$\mathbb{U}\ll \mathbf{D(X)}$
. By Proposition 4.12,
![]() $\textrm{Max}(\mathbb{U})=\mathbb{U}\cap \textrm{Max}\mathbf{D(X)}$
is a finite set, and we may assume
$\textrm{Max}(\mathbb{U})=\mathbb{U}\cap \textrm{Max}\mathbf{D(X)}$
is a finite set, and we may assume
![]() $\textrm{Max}(\mathbb{U}):=\{(\vec{x},\vec{x}):x\in F\}$
, where
$\textrm{Max}(\mathbb{U}):=\{(\vec{x},\vec{x}):x\in F\}$
, where
![]() $F$
is a finite subset of
$F$
is a finite subset of
![]() $X$
. Then, by Remark 4.4(1),
$X$
. Then, by Remark 4.4(1),
![]() $F=h^{-1}(\textrm{Max}(\mathbb{U}))\in \mathcal{O}(X)$
. Note that
$F=h^{-1}(\textrm{Max}(\mathbb{U}))\in \mathcal{O}(X)$
. Note that
![]() $F\neq \emptyset$
because
$F\neq \emptyset$
because
![]() $\mathbb{U}\neq \emptyset$
. Choose a point
$\mathbb{U}\neq \emptyset$
. Choose a point
![]() $x\in F\neq \emptyset$
. Then, as
$x\in F\neq \emptyset$
. Then, as
![]() $X$
is
$X$
is
![]() $T_1$
space, the finite set
$T_1$
space, the finite set
![]() $F\setminus \{x\}$
is closed, so the singleton set
$F\setminus \{x\}$
is closed, so the singleton set
![]() $\{x\}=F\setminus (F\setminus \{x\})$
is open, contradicting
$\{x\}=F\setminus (F\setminus \{x\})$
is open, contradicting
![]() $X_{\textrm{iso}}=\emptyset$
. Therefore,
$X_{\textrm{iso}}=\emptyset$
. Therefore,
![]() $\Sigma \mathbf{D(X)}$
is a routine space.
$\Sigma \mathbf{D(X)}$
is a routine space.
(2)
![]() $\Rightarrow$
(1): Assume, on the contrary, there exists a point
$\Rightarrow$
(1): Assume, on the contrary, there exists a point
![]() $x\in X_{\textrm{iso}}$
. Then, by Lemma 4.8,
$x\in X_{\textrm{iso}}$
. Then, by Lemma 4.8,
![]() $\emptyset \neq{\mathord{\uparrow }} (\vec{X}_{\textrm{iso}},\vec{x})\in \sigma (\mathbf{D(X)})$
and
$\emptyset \neq{\mathord{\uparrow }} (\vec{X}_{\textrm{iso}},\vec{x})\in \sigma (\mathbf{D(X)})$
and
![]() ${\mathord{\uparrow }} (\vec{X}_{\textrm{iso}},\vec{x})\ll{\mathord{\uparrow }} (\vec{X}_{\textrm{iso}},\vec{x})\subseteq \mathbf{D(X)}$
. Thus,
${\mathord{\uparrow }} (\vec{X}_{\textrm{iso}},\vec{x})\ll{\mathord{\uparrow }} (\vec{X}_{\textrm{iso}},\vec{x})\subseteq \mathbf{D(X)}$
. Thus,
![]() $\emptyset \neq{\mathord{\uparrow }} (\vec{X}_{\textrm{iso}},\vec{x})\ll \mathbf{D(X)}$
, contradicting assumption (2). Therefore,
$\emptyset \neq{\mathord{\uparrow }} (\vec{X}_{\textrm{iso}},\vec{x})\ll \mathbf{D(X)}$
, contradicting assumption (2). Therefore,
![]() $X_{\textrm{iso}}=\emptyset$
.
$X_{\textrm{iso}}=\emptyset$
.
The following result is clear from the above theorem, which strengthens Corollary 4.16.
Corollary 4.20.
The Scott space
![]() $\Sigma \mathbf D(\mathbb{N}_{cof})$
is a routine space.
$\Sigma \mathbf D(\mathbb{N}_{cof})$
is a routine space.
By Corollary 4.14, Theorems4.6 and 4.19, we have the following results.
Theorem 4.21.
Every
![]() $T_1$
space containing at least one isolated point has a non-routine open well-filtered dcpo model.
$T_1$
space containing at least one isolated point has a non-routine open well-filtered dcpo model.
Theorem 4.22.
Every
![]() $T_1$
space containing a finite nonempty set of isolated points has a non-routine strongly core-coherent open well-filtered dcpo model.
$T_1$
space containing a finite nonempty set of isolated points has a non-routine strongly core-coherent open well-filtered dcpo model.
By Theorem 3 in Xi and Zhao (Reference Xi and Zhao2017) (saying that a
![]() $T_1$
space is well-filtered iff its Xi-Zhao model is well-filtered), we obtain the following corollary, which provides a general approach to construct a non-routine open well-filtered but not well-filtered dcpo.
$T_1$
space is well-filtered iff its Xi-Zhao model is well-filtered), we obtain the following corollary, which provides a general approach to construct a non-routine open well-filtered but not well-filtered dcpo.
Corollary 4.23.
Let
![]() $X$
be a
$X$
be a
![]() $T_1$
space. If
$T_1$
space. If
![]() $X$
is not well-filtered and
$X$
is not well-filtered and
![]() $X_{\textrm{iso}}\neq \emptyset$
, then
$X_{\textrm{iso}}\neq \emptyset$
, then
![]() $\mathbf{D(X)}$
is a non-routine open well-filtered, but not well-filtered dcpo.
$\mathbf{D(X)}$
is a non-routine open well-filtered, but not well-filtered dcpo.
4.4 Some examples
Before presenting the example, we will introduce some concepts and properties related to the sum (or co-product) of topological spaces, which will be used later.
Definition 4.24.
Suppose
![]() $X$
and
$X$
and
![]() $Y$
are two disjoint topological spaces, that is,
$Y$
are two disjoint topological spaces, that is,
![]() $X\cap Y=\emptyset$
. The set
$X\cap Y=\emptyset$
. The set
![]() $Z=X\cup Y$
with the topology
$Z=X\cup Y$
with the topology
is called the sum (co-product) of the spaces
![]() $X$
and
$X$
and
![]() $Y$
, denoted by
$Y$
, denoted by
![]() $X\oplus Y$
.
$X\oplus Y$
.
Lemma 4.25 ((Engelking, Reference Engelking1989, Theorem 2.2.7)). The sum
![]() $X\oplus Y$
is
$X\oplus Y$
is
![]() $T_0$
(resp.,
$T_0$
(resp.,
![]() $T_1$
) whenever
$T_1$
) whenever
![]() $X$
and
$X$
and
![]() $Y$
are
$Y$
are
![]() $T_0$
(resp.,
$T_0$
(resp.,
![]() $T_1$
) spaces.
$T_1$
) spaces.
Lemma 4.26.
Let
![]() $X$
and
$X$
and
![]() $Y$
be two disjoint topological spaces, and
$Y$
be two disjoint topological spaces, and
![]() $U,V\in \mathcal{O}(X\oplus Y)$
. Then, the following conditions are equivalent:
$U,V\in \mathcal{O}(X\oplus Y)$
. Then, the following conditions are equivalent:
-
(1)
 $U\ll V$
in
$U\ll V$
in
 $\mathcal{O}(X\oplus Y)$
.
$\mathcal{O}(X\oplus Y)$
. -
(2)
 $U\cap X\ll V\cap X$
in
$U\cap X\ll V\cap X$
in
 $\mathcal{O}(X)$
and
$\mathcal{O}(X)$
and
 $U\cap Y\ll V\cap Y$
in
$U\cap Y\ll V\cap Y$
in
 $\mathcal{O}(Y)$
.
$\mathcal{O}(Y)$
.
Proof.
(1)
![]() $\Rightarrow$
(2): We only verify
$\Rightarrow$
(2): We only verify
![]() $U\cap X\ll V\cap X$
, as the proof for
$U\cap X\ll V\cap X$
, as the proof for
![]() $U\cap Y\ll V\cap Y$
is similar. Suppose
$U\cap Y\ll V\cap Y$
is similar. Suppose
![]() $\{V_i:i\in I\}\subseteq \mathcal{O}(X)$
is an open cover of
$\{V_i:i\in I\}\subseteq \mathcal{O}(X)$
is an open cover of
![]() $V\cap X$
. Then,
$V\cap X$
. Then,
![]() $V=(V\cap X)\cup (V\cap Y)\subseteq (V\cap X)\cup Y\subseteq \bigcup _{i\in I}(V_i\cup Y)$
, which implies that
$V=(V\cap X)\cup (V\cap Y)\subseteq (V\cap X)\cup Y\subseteq \bigcup _{i\in I}(V_i\cup Y)$
, which implies that
![]() $\{V_i\cup Y:i\in I\}\subseteq \mathcal{O} (X\oplus Y)$
. As
$\{V_i\cup Y:i\in I\}\subseteq \mathcal{O} (X\oplus Y)$
. As
![]() $U\ll V$
, there exists a finite subset
$U\ll V$
, there exists a finite subset
![]() $J\subseteq I$
such that
$J\subseteq I$
such that
![]() $U\subseteq \bigcup _{j\in J}(V_j\cup Y)$
. Note that
$U\subseteq \bigcup _{j\in J}(V_j\cup Y)$
. Note that
![]() $X\cap Y=\emptyset$
and
$X\cap Y=\emptyset$
and
![]() $V_i\subseteq X$
for all
$V_i\subseteq X$
for all
![]() $i\in I$
, so
$i\in I$
, so
![]() $U\cap X\subseteq \bigcup _{j\in J}((V_j\cap X)\cup (Y\cap X))=\bigcup _{j\in J}(V_j\cap X)=\bigcup _{j\in J}V_j$
. This shows that
$U\cap X\subseteq \bigcup _{j\in J}((V_j\cap X)\cup (Y\cap X))=\bigcup _{j\in J}(V_j\cap X)=\bigcup _{j\in J}V_j$
. This shows that
![]() $U\cap X\ll V\cap X$
.
$U\cap X\ll V\cap X$
.
(2)
![]() $\Rightarrow$
(1): Suppose
$\Rightarrow$
(1): Suppose
![]() $\{V_i:i\in I\}\subseteq \mathcal{O}(X\oplus Y)$
is an open cover of
$\{V_i:i\in I\}\subseteq \mathcal{O}(X\oplus Y)$
is an open cover of
![]() $V$
. Then, it is clear that
$V$
. Then, it is clear that
![]() $\{V_i\cap X:i\in I\}\subseteq \mathcal{O}(X)$
is an open cover of
$\{V_i\cap X:i\in I\}\subseteq \mathcal{O}(X)$
is an open cover of
![]() $V\cap X$
and
$V\cap X$
and
![]() $\{V_i\cap Y:i\in I\}\subseteq \mathcal{O}(Y)$
is an open cover of
$\{V_i\cap Y:i\in I\}\subseteq \mathcal{O}(Y)$
is an open cover of
![]() $V\cap Y$
. Since
$V\cap Y$
. Since
![]() $U\cap X\ll V\cap X$
and
$U\cap X\ll V\cap X$
and
![]() $U\cap Y\ll V\cap Y$
, there exist finite subsets
$U\cap Y\ll V\cap Y$
, there exist finite subsets
![]() $J_1,J_2\subseteq I$
such that
$J_1,J_2\subseteq I$
such that
![]() $U\cap X\subseteq \bigcup _{j\in J_1}V_j\cap X$
and
$U\cap X\subseteq \bigcup _{j\in J_1}V_j\cap X$
and
![]() $U\cap Y\subseteq \bigcup _{j\in J_2}V_j\cap Y$
. Let
$U\cap Y\subseteq \bigcup _{j\in J_2}V_j\cap Y$
. Let
![]() $J:=J_1\cup J_2$
, which is a finite set. Then,
$J:=J_1\cup J_2$
, which is a finite set. Then,
![]() $U=(U\cap X)\cup (U\cap Y)\subseteq (\bigcup _{j\in J_1}V_j\cap X)\cup (\bigcup _{j\in J_2}V_j\cap Y)\subseteq \bigcup _{j\in J}V_j$
. This shows that
$U=(U\cap X)\cup (U\cap Y)\subseteq (\bigcup _{j\in J_1}V_j\cap X)\cup (\bigcup _{j\in J_2}V_j\cap Y)\subseteq \bigcup _{j\in J}V_j$
. This shows that
![]() $U\ll V$
.
$U\ll V$
.
Lemma 4.27.
Let
![]() $X$
and
$X$
and
![]() $Y$
be two disjoint topological spaces, and
$Y$
be two disjoint topological spaces, and
![]() $K\subseteq X\oplus Y$
. Then, the following conditions are equivalent:
$K\subseteq X\oplus Y$
. Then, the following conditions are equivalent:
-
(1)
 $K$
is a compact set in
$K$
is a compact set in
 $X\oplus Y$
.
$X\oplus Y$
. -
(2)
 $K\cap X$
and
$K\cap X$
and
 $K\cap Y$
are compact sets in
$K\cap Y$
are compact sets in
 $X$
and
$X$
and
 $Y$
, respectively.
$Y$
, respectively.
Proof. The proof is analogous to Lemma 4.26.
In the following, we provide an example of non-routine open well-filtered but not well-filtered dcpo.
Example 4.28.
Recall that
![]() $\mathbb{N}$
is the set of all positive integers. Let
$\mathbb{N}$
is the set of all positive integers. Let
![]() $Y:=\{\frac{1}{k}: k\in \mathbb{N}\setminus \{1\}\}\cup \{0\}$
be the subspace of the real line with the usual topology. Note that
$Y:=\{\frac{1}{k}: k\in \mathbb{N}\setminus \{1\}\}\cup \{0\}$
be the subspace of the real line with the usual topology. Note that
![]() $Y\cap \mathbb{N} =\emptyset$
. Let
$Y\cap \mathbb{N} =\emptyset$
. Let
![]() $X:=Y\oplus (\mathbb{N})_{cof}$
be the sum of spaces
$X:=Y\oplus (\mathbb{N})_{cof}$
be the sum of spaces
![]() $Y$
and
$Y$
and
![]() $(\mathbb{N})_{cof}$
.
$(\mathbb{N})_{cof}$
.
-
(1)
 $X$
is a strongly core-coherent (and hence core-coherent)
$X$
is a strongly core-coherent (and hence core-coherent)
 $T_1$
space.
$T_1$
space.
— As
 $Y$
and
$Y$
and
 $(\mathbb{N})_{cof}$
are both
$(\mathbb{N})_{cof}$
are both
 $T_1$
spaces, by Lemma 4.25
, we know that
$T_1$
spaces, by Lemma 4.25
, we know that
 $X$
is a
$X$
is a
 $T_1$
space.
$T_1$
space.
Before proving
 $X$
is strongly core-coherent, we give a property on
$X$
is strongly core-coherent, we give a property on
 $Y$
.
$Y$
.Claim: If
 $U\ll V$
in
$U\ll V$
in
 $\mathcal{O}(Y)$
and
$\mathcal{O}(Y)$
and
 $0\notin V$
, then
$0\notin V$
, then
 $U$
is a finite set.
$U$
is a finite set.
This is trivial since each single set
 $\{\frac{1}{k}\}$
,
$\{\frac{1}{k}\}$
,
 $k\geq 2$
, is open in
$k\geq 2$
, is open in
 $Y$
. Therefore,
$Y$
. Therefore,
 $\{\{x\}:x\in V\}$
is an open cover of
$\{\{x\}:x\in V\}$
is an open cover of
 $V$
, so there exists a finite set
$V$
, so there exists a finite set
 $F\subseteq V$
such that
$F\subseteq V$
such that
 $U\subseteq F$
. Hence,
$U\subseteq F$
. Hence,
 $U$
is finite.
$U$
is finite.
To show
 $X$
is strongly core-coherent, assume
$X$
is strongly core-coherent, assume
 $U_1,U_2,V\in \mathcal{O}(X)$
such that
$U_1,U_2,V\in \mathcal{O}(X)$
such that
 $U_1\ll U_2$
. We need to prove that
$U_1\ll U_2$
. We need to prove that
 $U_1\cap V\ll U_2\cap V$
, and we will prove this by using Lemma 4.26
. Since every set in
$U_1\cap V\ll U_2\cap V$
, and we will prove this by using Lemma 4.26
. Since every set in
 $(\mathbb{N})_{cof}$
is compact, we have that
$(\mathbb{N})_{cof}$
is compact, we have that
 $U_1\cap V\cap \mathbb{N}\ll U_2\cap V\cap \mathbb{N}$
. It remains to prove that
$U_1\cap V\cap \mathbb{N}\ll U_2\cap V\cap \mathbb{N}$
. It remains to prove that
 $U_1\cap V\cap Y\ll U_2\cap V\cap Y$
. For this purpose, suppose
$U_1\cap V\cap Y\ll U_2\cap V\cap Y$
. For this purpose, suppose
 $\{U_i:i\in I\}\subseteq \mathcal{O}(Y)$
is an open cover of
$\{U_i:i\in I\}\subseteq \mathcal{O}(Y)$
is an open cover of
 $U_2\cap V\cap Y$
. There are two cases:
$U_2\cap V\cap Y$
. There are two cases:
(c1)
 $0\in U_2\cap V\cap Y$
. Then, there exists
$0\in U_2\cap V\cap Y$
. Then, there exists
 $i_{0}$
such that
$i_{0}$
such that
 $0\in U_{i_0}$
. Observe that the complement set
$0\in U_{i_0}$
. Observe that the complement set
 $Y\setminus U$
of every open neighborhood
$Y\setminus U$
of every open neighborhood
 $U$
of
$U$
of
 $0$
in
$0$
in
 $Y$
is finite, so
$Y$
is finite, so
 $F:=(U_1\cap V\cap Y)\setminus U_{i_0}\subseteq Y\setminus U_{i_0}$
is finite. Note that
$F:=(U_1\cap V\cap Y)\setminus U_{i_0}\subseteq Y\setminus U_{i_0}$
is finite. Note that
 $F\subseteq \bigcup _{i\in I\setminus \{i_0\}}U_i$
, there exists a finite subset
$F\subseteq \bigcup _{i\in I\setminus \{i_0\}}U_i$
, there exists a finite subset
 $J\subseteq I\setminus \{i_0\}$
such that
$J\subseteq I\setminus \{i_0\}$
such that
 $F\subseteq \bigcup _{j\in J}U_j$
. Then, we have that
$F\subseteq \bigcup _{j\in J}U_j$
. Then, we have that
 $U_1\cap V\cap Y\subseteq F\cup U_{i_0}\subseteq \bigcup _{j\in J\cup \{i_0\}}U_j$
.
$U_1\cap V\cap Y\subseteq F\cup U_{i_0}\subseteq \bigcup _{j\in J\cup \{i_0\}}U_j$
.(c2)
 $0\notin U_2\cap V\cap Y$
. Since
$0\notin U_2\cap V\cap Y$
. Since
 $U_1\ll U_2$
, by Lemma 4.26
,
$U_1\ll U_2$
, by Lemma 4.26
,
 $U_1\cap Y\ll U_2\cap Y$
in
$U_1\cap Y\ll U_2\cap Y$
in
 $\mathcal{O}(Y)$
. From the claim it follows that
$\mathcal{O}(Y)$
. From the claim it follows that
 $U_1\cap Y$
is a finite set, so is
$U_1\cap Y$
is a finite set, so is
 $U_1\cap V\cap Y$
. Thus, there exists a finite subset
$U_1\cap V\cap Y$
. Thus, there exists a finite subset
 $J\subseteq I\setminus \{i_0\}$
such that
$J\subseteq I\setminus \{i_0\}$
such that
 $U_1\cap V\cap Y\subseteq \bigcup _{j\in J}U_j$
.
$U_1\cap V\cap Y\subseteq \bigcup _{j\in J}U_j$
.From (c1) and (c2), we deduce that
 $U_1\cap V\cap Y\ll U_2\cap V\cap Y$
in
$U_1\cap V\cap Y\ll U_2\cap V\cap Y$
in
 $\mathcal{O}(Y)$
. Thus, by Lemma 4.26
,
$\mathcal{O}(Y)$
. Thus, by Lemma 4.26
,
 $U_1\cap V\ll U_2\cap V$
in
$U_1\cap V\ll U_2\cap V$
in
 $\mathcal{O}(X)$
. Therefore,
$\mathcal{O}(X)$
. Therefore,
 $X$
is strongly core-coherent.
$X$
is strongly core-coherent.
-
(2)
 $\Sigma \mathbf{D(X)}$
is not core-coherent, and hence is not strongly core-coherent.
$\Sigma \mathbf{D(X)}$
is not core-coherent, and hence is not strongly core-coherent.
It is trivial by Theorem 4.13 and that
 $X_{\textrm{iso}}:=Y\setminus \{0\}$
is infinite.
$X_{\textrm{iso}}:=Y\setminus \{0\}$
is infinite.
-
(3)
 $\Sigma \mathbf{D(X)}$
is a non-routine open well-filtered space.
$\Sigma \mathbf{D(X)}$
is a non-routine open well-filtered space.
— Note that
 $X_{\textrm{iso}}:=Y\setminus \{0\}\neq \emptyset$
. Thus, by Theorem
4.19
,
$X_{\textrm{iso}}:=Y\setminus \{0\}\neq \emptyset$
. Thus, by Theorem
4.19
,
 $\Sigma \mathbf{D(X)}$
is a non-routine open well-filtered space.
$\Sigma \mathbf{D(X)}$
is a non-routine open well-filtered space.
-
(4)
 $\Sigma \mathbf{D(X)}$
is not well-filtered.
$\Sigma \mathbf{D(X)}$
is not well-filtered.
— Let
 $A_k=\{n\in \mathbb{N}:n\geq k\}$
for each
$A_k=\{n\in \mathbb{N}:n\geq k\}$
for each
 $k\in \mathbb{N}$
. Then, the family
$k\in \mathbb{N}$
. Then, the family
 $\{A_k:k\in \mathbb{N}\}$
is a filtered family of compact (automatically saturated) sets in
$\{A_k:k\in \mathbb{N}\}$
is a filtered family of compact (automatically saturated) sets in
 $(\mathbb{N})_{cof}$
and, by Lemma 4.27
, in
$(\mathbb{N})_{cof}$
and, by Lemma 4.27
, in
 $X$
as well. Since
$X$
as well. Since
 $\bigcap _{k\in \mathbb{N}}A_k=\emptyset$
and
$\bigcap _{k\in \mathbb{N}}A_k=\emptyset$
and
 $A_k\neq \emptyset$
for any
$A_k\neq \emptyset$
for any
 $k\in \mathbb{N}$
, it follows that
$k\in \mathbb{N}$
, it follows that
 $X$
is not well-filtered. By Theorem 3 in Xi and Zhao (Reference Xi and Zhao2017) (saying that a
$X$
is not well-filtered. By Theorem 3 in Xi and Zhao (Reference Xi and Zhao2017) (saying that a
 $T_1$
space is well-filtered iff its Xi-Zhao model is well-filtered), we conclude that
$T_1$
space is well-filtered iff its Xi-Zhao model is well-filtered), we conclude that
 $\Sigma \mathbf{D(X)}$
is not well-filtered.
$\Sigma \mathbf{D(X)}$
is not well-filtered.
We can deduce the following two main corollaries from the example above.
Corollary 4.29. There exists a non-routine open well-filtered, but not well-filtered dcpo.
Corollary 4.30. Neither core-coherence nor strong core-coherence is preserved by the Xi-Zhao model.
Next, we show that for a
![]() $T_1$
space
$T_1$
space
![]() $X$
, the properties of
$X$
, the properties of
![]() $|X_{\textrm{iso}}|\lt \omega$
and being (strongly) core-coherent are independent, as illustrated by the following example.
$|X_{\textrm{iso}}|\lt \omega$
and being (strongly) core-coherent are independent, as illustrated by the following example.
Example 4.31.
-
(1)
 $|X_{\textrm{iso}}|\lt \omega$
$|X_{\textrm{iso}}|\lt \omega$
 $\nRightarrow$
$\nRightarrow$
 $X$
is strongly core-coherent.
$X$
is strongly core-coherent.
— Consider the set
 $[0,1]$
with the usual topology, that is, the base open sets are of the forms
$[0,1]$
with the usual topology, that is, the base open sets are of the forms
 $[0,r)$
and
$[0,r)$
and
 $(s,1]$
for
$(s,1]$
for
 $s,t\in [0,1]$
. It is clear that
$s,t\in [0,1]$
. It is clear that
 $[0,1]_{\textrm{iso}}=\emptyset$
, so
$[0,1]_{\textrm{iso}}=\emptyset$
, so
 $|[0,1]_{\textrm{iso}}|\lt \omega$
. However, it is not strongly core-coherent, as shown in Example 3.7.
$|[0,1]_{\textrm{iso}}|\lt \omega$
. However, it is not strongly core-coherent, as shown in Example 3.7. -
(2)
 $X$
is strongly core-coherent
$X$
is strongly core-coherent
 $\nRightarrow$
$\nRightarrow$
 $|X_{\textrm{iso}}|\lt \omega$
.
$|X_{\textrm{iso}}|\lt \omega$
.— Consider the space
 $X$
in Example 4.28. It has been proved that
$X$
in Example 4.28. It has been proved that
 $X$
is strongly core-coherent. Additionally, we have
$X$
is strongly core-coherent. Additionally, we have
 $|X_{\textrm{iso}}|=|Y_{\textrm{iso}}| + |(\mathbb{N}_{cof})_{\textrm{iso}}|=\omega + 0=\omega \not \lt \omega$
.
$|X_{\textrm{iso}}|=|Y_{\textrm{iso}}| + |(\mathbb{N}_{cof})_{\textrm{iso}}|=\omega + 0=\omega \not \lt \omega$
.
At the end of the paper, we present a counterexample demonstrating that wb-sober spaces need not be open well-filtered, which also serves as part of the proof of Theorem3.11.
Example 4.32.
Let
![]() $ X = \{x_n : n \in \mathbb{N}\}$
and
$ X = \{x_n : n \in \mathbb{N}\}$
and
![]() $ Y = \{y_n : n \in \mathbb{N}\}$
be two chains with the following orders:
$ Y = \{y_n : n \in \mathbb{N}\}$
be two chains with the following orders:
and
Let
![]() $\mathbb{J}^*=\mathbb{N}\times (\mathbb{N}\cup \{\infty \})\times \{*\}$
be the dcpo that is order-isomorphic to the Johnstone’s dcpo
$\mathbb{J}^*=\mathbb{N}\times (\mathbb{N}\cup \{\infty \})\times \{*\}$
be the dcpo that is order-isomorphic to the Johnstone’s dcpo
![]() $\mathbb{J}$
(see Example 3.15) via the mapping
$\mathbb{J}$
(see Example 3.15) via the mapping
![]() $(m,n,*)\mapsto (m,n)$
,
$(m,n,*)\mapsto (m,n)$
,
![]() $\forall (m,n,*)\in \mathbb{J}^*$
.
$\forall (m,n,*)\in \mathbb{J}^*$
.
Let
![]() $P=\mathbb{J}\cup X\cup Y\cup \mathbb{J}^*$
. We define a partial order
$P=\mathbb{J}\cup X\cup Y\cup \mathbb{J}^*$
. We define a partial order
![]() $\leq$
on
$\leq$
on
![]() $P$
as follows:
$P$
as follows:
-
(i) all
 $\mathbb{J}$
,
$\mathbb{J}$
,
 $X$
,
$X$
,
 $Y$
and
$Y$
and
 $\mathbb{J}^*$
are subposets of
$\mathbb{J}^*$
are subposets of
 $P$
;
$P$
; -
(ii)
 $\forall n\in \mathbb{N}$
,
$\forall n\in \mathbb{N}$
,
 $(k,n)\leq x_n\leq (2m-1, n,*)$
for all
$(k,n)\leq x_n\leq (2m-1, n,*)$
for all
 $k,m\in \mathbb{N}$
;
$k,m\in \mathbb{N}$
; -
(iii)
 $\forall n\in \mathbb{N}$
,
$\forall n\in \mathbb{N}$
,
 $y_n\leq (2m,n,*)$
for all
$y_n\leq (2m,n,*)$
for all
 $m\in \mathbb{N}$
.
$m\in \mathbb{N}$
.
The following conditions are clear by (ii):
-
(iv)
 $\forall n\in \mathbb{N}$
,
$\forall n\in \mathbb{N}$
,
 $(k,n)\leq (2m-1, n,*)$
for all
$(k,n)\leq (2m-1, n,*)$
for all
 $k,m\in \mathbb{N}$
;
$k,m\in \mathbb{N}$
; -
(v)
 $(k,\infty )=\bigvee _{n\in \mathbb{N}}(k,n)\leq \bigvee _{n\in \mathbb{N}}(2m-1,n,*)= (2m-1,\infty, *)$
for all
$(k,\infty )=\bigvee _{n\in \mathbb{N}}(k,n)\leq \bigvee _{n\in \mathbb{N}}(2m-1,n,*)= (2m-1,\infty, *)$
for all
 $k,m\in \mathbb{N}$
.
$k,m\in \mathbb{N}$
.
The poset
![]() $P$
is illustrated in Figure
4
. In particular, the order on the
$P$
is illustrated in Figure
4
. In particular, the order on the
![]() $n$
-level of
$n$
-level of
![]() $P$
is illustrated in Figure
5
.
$P$
is illustrated in Figure
5
.

Figure 4. The poset
![]() $P$
in Example 4.32.
$P$
in Example 4.32.

Figure 5. The order on the
![]() $n$
-level of
$n$
-level of
![]() $P$
in Example 4.32.
$P$
in Example 4.32.
-
(1)
 $\Sigma P$
is not open well-filtered.
$\Sigma P$
is not open well-filtered.
— For each
 $ n \in \mathbb{N}$
, it is easy to verify that
$ n \in \mathbb{N}$
, it is easy to verify that
 $ \uparrow \{x_n, y_n\}$
is a Scott open subset of
$ \uparrow \{x_n, y_n\}$
is a Scott open subset of
 $ P$
. Moreover,
$ P$
. Moreover,
 $ \uparrow \{x_{n+1}, y_{n+1}\} \ll \uparrow \{x_n, y_n\}$
in
$ \uparrow \{x_{n+1}, y_{n+1}\} \ll \uparrow \{x_n, y_n\}$
in
 $ (\sigma (P), \subseteq )$
, as these are compact open sets. Thus,
$ (\sigma (P), \subseteq )$
, as these are compact open sets. Thus,
 $ \mathcal{F} := \{\uparrow \{x_n, y_n\} : n \in \mathbb{N}\}$
is a
$ \mathcal{F} := \{\uparrow \{x_n, y_n\} : n \in \mathbb{N}\}$
is a
 $ \ll$
-filtered subfamily of
$ \ll$
-filtered subfamily of
 $ \sigma (P)$
. Define
$ \sigma (P)$
. Define
 $U:=\bigcup _{n\in \mathbb{N}}{\mathord{\uparrow }}(n,n,*)$
, which is a Scott open set in
$U:=\bigcup _{n\in \mathbb{N}}{\mathord{\uparrow }}(n,n,*)$
, which is a Scott open set in
 $\Sigma \mathbb{J}^*$
. Note that
$\Sigma \mathbb{J}^*$
. Note that
 $\mathbb{J}^*$
is a Scott open subset of
$\mathbb{J}^*$
is a Scott open subset of
 $P$
, and then the Scott topology on
$P$
, and then the Scott topology on
 $\mathbb{J}^*$
agrees with the relative Scott topology from
$\mathbb{J}^*$
agrees with the relative Scott topology from
 $P$
(Gierz et al. 2003, Exercise II-1.26.). Thus,
$P$
(Gierz et al. 2003, Exercise II-1.26.). Thus,
 $U$
is a Scott open subset of
$U$
is a Scott open subset of
 $P$
. We have that
$P$
. We have that
 $\bigcap \mathcal{F}=\{(n,\infty, *):n\in \mathbb{N}\}\subseteq U$
, while
$\bigcap \mathcal{F}=\{(n,\infty, *):n\in \mathbb{N}\}\subseteq U$
, while
 ${\mathord{\uparrow }}\{x_n,y_n\}\nsubseteq U$
as
${\mathord{\uparrow }}\{x_n,y_n\}\nsubseteq U$
as
 $(n+1,n,*)\in{\mathord{\uparrow }}\{x_n,y_n\}\setminus U$
for each
$(n+1,n,*)\in{\mathord{\uparrow }}\{x_n,y_n\}\setminus U$
for each
 $n\in \mathbb{N}$
. Therefore,
$n\in \mathbb{N}$
. Therefore,
 $\Sigma P$
is not open well-filtered.
$\Sigma P$
is not open well-filtered.
-
(2)
 $\Sigma P$
is wb-sober.
$\Sigma P$
is wb-sober.
We prove this in some steps.
Step 1: We show some basic results on
 $P$
.
$P$
.-
(i)
 $\forall U\in \sigma (P)$
,
$\forall U\in \sigma (P)$
,
 $U\neq \emptyset$
iff
$U\neq \emptyset$
iff
 $U\cap \mathbb{J}^*\neq \emptyset$
.
$U\cap \mathbb{J}^*\neq \emptyset$
.— Note that
 $P={\mathord{\downarrow }} \mathbb{J}^*$
. Thus,
$P={\mathord{\downarrow }} \mathbb{J}^*$
. Thus,
 $U\neq \emptyset$
iff
$U\neq \emptyset$
iff
 $U\cap{\mathord{\downarrow }} \mathbb{J}^*\neq \emptyset$
, which is equivalent to
$U\cap{\mathord{\downarrow }} \mathbb{J}^*\neq \emptyset$
, which is equivalent to
 $U\cap \mathbb{J}^*\neq \emptyset$
since
$U\cap \mathbb{J}^*\neq \emptyset$
since
 $U={\mathord{\uparrow }} U$
.
$U={\mathord{\uparrow }} U$
. -
(ii)
 $Y\cup \mathbb{J}^*$
is a Scott open subset of
$Y\cup \mathbb{J}^*$
is a Scott open subset of
 $P$
.
$P$
.— Note that the complement
 $P \setminus (Y \cup \mathbb{J}^*) = X \cup \mathbb{J}$
is Scot closed, since it is clear a lower set and closed for the suprema of directed sets.
$P \setminus (Y \cup \mathbb{J}^*) = X \cup \mathbb{J}$
is Scot closed, since it is clear a lower set and closed for the suprema of directed sets.
-
(iii) Suppose
 $C_1=\mathbb{J}\cup X\cup{\mathord{\downarrow }} \{(2m_i-1,n_i,*):i\in I\}$
and
$C_1=\mathbb{J}\cup X\cup{\mathord{\downarrow }} \{(2m_i-1,n_i,*):i\in I\}$
and
 $C_2={\mathord{\downarrow }}\{(2m_i,n_i,*):i\in I\}$
, where all
$C_2={\mathord{\downarrow }}\{(2m_i,n_i,*):i\in I\}$
, where all
 $m_i,n_i$
are elements of
$m_i,n_i$
are elements of
 $\mathbb{N}$
and
$\mathbb{N}$
and
 $m_j\neq m_k$
whenever
$m_j\neq m_k$
whenever
 $j\neq k$
for
$j\neq k$
for
 $j,k\in I$
. Then, both
$j,k\in I$
. Then, both
 $C_1$
and
$C_1$
and
 $C_2$
are Scott closed subsets of
$C_2$
are Scott closed subsets of
 $P$
.
$P$
.— It is clear.
Step 2:
 $U\ll P\setminus Y$
in
$U\ll P\setminus Y$
in
 $(\sigma (P),\subseteq )$
iff
$(\sigma (P),\subseteq )$
iff
 $U=\emptyset$
.
$U=\emptyset$
.— First, it is clear that
 $Y$
is Scott closed, and thus
$Y$
is Scott closed, and thus
 $P\setminus Y\in \sigma (P)$
. In addition,
$P\setminus Y\in \sigma (P)$
. In addition,
 $\emptyset \ll P\setminus Y$
is trivial. Now assume
$\emptyset \ll P\setminus Y$
is trivial. Now assume
 $U\in \sigma (P)$
and
$U\in \sigma (P)$
and
 $U\neq \emptyset$
. We will prove that
$U\neq \emptyset$
. We will prove that
 $U\not \ll P\setminus Y$
by using Remark 2.5
. Since
$U\not \ll P\setminus Y$
by using Remark 2.5
. Since
 $U\neq \emptyset$
, by Step 1 (i),
$U\neq \emptyset$
, by Step 1 (i),
 $U\cap \mathbb{J}^*\neq \emptyset$
. Note that
$U\cap \mathbb{J}^*\neq \emptyset$
. Note that
 $\mathbb{J}^*$
is a Scott open subset of
$\mathbb{J}^*$
is a Scott open subset of
 $P$
, and thus the Scott topology on
$P$
, and thus the Scott topology on
 $\mathbb{J}^*$
agrees with the relative Scott topology from
$\mathbb{J}^*$
agrees with the relative Scott topology from
 $P$
(Gierz et al. 2003, Exercise II-1.26.). Then,
$P$
(Gierz et al. 2003, Exercise II-1.26.). Then,
 $U\cap \mathbb{J}^*\in \sigma (\mathbb{J}^*)$
, which is of form
$U\cap \mathbb{J}^*\in \sigma (\mathbb{J}^*)$
, which is of form
 $\bigcup _{k\in \mathbb{N}\setminus F}{\mathord{\uparrow }}(k,\phi (k),*)$
, where
$\bigcup _{k\in \mathbb{N}\setminus F}{\mathord{\uparrow }}(k,\phi (k),*)$
, where
 $F$
is a finite subset of
$F$
is a finite subset of
 $\mathbb{N}$
and
$\mathbb{N}$
and
 $\phi (k)\in \mathbb{N}$
for each
$\phi (k)\in \mathbb{N}$
for each
 $k\in \mathbb{N}\setminus F$
. Let
$k\in \mathbb{N}\setminus F$
. Let
 $n_0$
be the greatest number in
$n_0$
be the greatest number in
 $F$
. For each
$F$
. For each
 $n\gt n_0$
, define
$n\gt n_0$
, define
 $C_{n}:={\mathord{\downarrow }}\{(2k,\phi (2k),*):k\geq n\}$
. Then, by Step 1 (iii),
$C_{n}:={\mathord{\downarrow }}\{(2k,\phi (2k),*):k\geq n\}$
. Then, by Step 1 (iii),
 $\{C_n:n\in \mathbb{N}\}$
is a filtered family of Scott closed subset of
$\{C_n:n\in \mathbb{N}\}$
is a filtered family of Scott closed subset of
 $P$
. It holds that
$P$
. It holds that
 $(P\setminus Y)\cap \bigcap _{n\gt n_0} C_n\subseteq (P\setminus Y)\cap Y =\emptyset$
and
$(P\setminus Y)\cap \bigcap _{n\gt n_0} C_n\subseteq (P\setminus Y)\cap Y =\emptyset$
and
 $(2n,\phi (2n),*)\in U\cap C_n\neq \emptyset$
for any
$(2n,\phi (2n),*)\in U\cap C_n\neq \emptyset$
for any
 $n\gt n_0$
. This shows that
$n\gt n_0$
. This shows that
 $U\not \ll P\setminus Y$
, completing the proof.
$U\not \ll P\setminus Y$
, completing the proof.
Step 3:
 $U\ll Y\cup \mathbb{J}^*$
in
$U\ll Y\cup \mathbb{J}^*$
in
 $(\sigma (P),\subseteq )$
iff
$(\sigma (P),\subseteq )$
iff
 $U=\emptyset$
.
$U=\emptyset$
.— By Step 1 (ii),
 $Y\cup \mathbb{J}^*\in \sigma (P)$
, and clearly
$Y\cup \mathbb{J}^*\in \sigma (P)$
, and clearly
 $\emptyset \ll Y\cup \mathbb{J}^*$
. Now assume
$\emptyset \ll Y\cup \mathbb{J}^*$
. Now assume
 $\emptyset \neq U\in \sigma (P)$
. We will prove that
$\emptyset \neq U\in \sigma (P)$
. We will prove that
 $U\not \ll Y\cup \mathbb{J}^*$
by using Remark 2.5
. First, using the same argument of Step 2,
$U\not \ll Y\cup \mathbb{J}^*$
by using Remark 2.5
. First, using the same argument of Step 2,
 $U\cap \mathbb{J}^*\in \sigma (\mathbb{J}^*)$
, which is of form
$U\cap \mathbb{J}^*\in \sigma (\mathbb{J}^*)$
, which is of form
 $\bigcup _{k\in \mathbb{N}\setminus F}{\mathord{\uparrow }}(k,\phi (k),*)$
, where
$\bigcup _{k\in \mathbb{N}\setminus F}{\mathord{\uparrow }}(k,\phi (k),*)$
, where
 $F$
is a finite subset of
$F$
is a finite subset of
 $\mathbb{N}$
and
$\mathbb{N}$
and
 $\phi (k)\in \mathbb{N}$
for any
$\phi (k)\in \mathbb{N}$
for any
 $k\in \mathbb{N}\setminus F$
. Let
$k\in \mathbb{N}\setminus F$
. Let
 $n_0$
be the greatest number in
$n_0$
be the greatest number in
 $F$
. For each
$F$
. For each
 $n\gt n_0$
, define
$n\gt n_0$
, define
 $C_{n}:=\mathbb{J}\cup X\cup{\mathord{\downarrow }}\{(2k-1,\phi (2k-1),*):k\geq n\}$
. Then, by Step 1 (iii),
$C_{n}:=\mathbb{J}\cup X\cup{\mathord{\downarrow }}\{(2k-1,\phi (2k-1),*):k\geq n\}$
. Then, by Step 1 (iii),
 $\{C_n:n\in \mathbb{N}\}$
is a filtered family of Scott closed subset of
$\{C_n:n\in \mathbb{N}\}$
is a filtered family of Scott closed subset of
 $P$
. It holds that
$P$
. It holds that
 $(Y\cup \mathbb{J}^*)\cap \bigcap _{n\gt n_0} C_n=(Y\cup \mathbb{J}^*)\cap \mathbb{J}\cup X=\emptyset$
, but
$(Y\cup \mathbb{J}^*)\cap \bigcap _{n\gt n_0} C_n=(Y\cup \mathbb{J}^*)\cap \mathbb{J}\cup X=\emptyset$
, but
 $(2n-1,\phi (2n-1),*)\in U\cap C_n\neq \emptyset$
for each
$(2n-1,\phi (2n-1),*)\in U\cap C_n\neq \emptyset$
for each
 $n\gt n_0$
. This shows that
$n\gt n_0$
. This shows that
 $U\not \ll Y\cup \mathbb{J}^*$
, completing the proof.
$U\not \ll Y\cup \mathbb{J}^*$
, completing the proof.
Step 4:
 $\Sigma P$
is wb-sober.
$\Sigma P$
is wb-sober.
— In fact, there are no wb-irreducible sets in
 $\Sigma P$
; consequently,
$\Sigma P$
; consequently,
 $\Sigma P$
is wb-sober. Now assume on the contrary that
$\Sigma P$
is wb-sober. Now assume on the contrary that
 $A$
is a wb-irreducible subset of
$A$
is a wb-irreducible subset of
 $P$
.
$P$
.Claim:
 $A\cap (P\setminus Y)=\emptyset$
.
$A\cap (P\setminus Y)=\emptyset$
.— Assume on the contrary that
 $A\cap (P\setminus Y)\neq \emptyset$
. Since
$A\cap (P\setminus Y)\neq \emptyset$
. Since
 $P\setminus Y\in \sigma (P)$
and
$P\setminus Y\in \sigma (P)$
and
 $A$
is wb-irreducible, there exists
$A$
is wb-irreducible, there exists
 $U\in \sigma (P)$
such that
$U\in \sigma (P)$
such that
 $U\ll (P\setminus Y)$
and
$U\ll (P\setminus Y)$
and
 $A\cap U\neq \emptyset$
. However, by Step 2,
$A\cap U\neq \emptyset$
. However, by Step 2,
 $U=\emptyset$
, contradicting that
$U=\emptyset$
, contradicting that
 $A\cap U\neq \emptyset$
. Therefore,
$A\cap U\neq \emptyset$
. Therefore,
 $A\cap (P\setminus Y)=\emptyset$
.
$A\cap (P\setminus Y)=\emptyset$
.Using the same argument and Step 3, we obtain that
 $A\cap (Y\cup \mathbb{J}^*)=\emptyset$
, which implies that
$A\cap (Y\cup \mathbb{J}^*)=\emptyset$
, which implies that
 $A\cap Y=\emptyset$
. From the claim, we can deduce that
$A\cap Y=\emptyset$
. From the claim, we can deduce that
 $A=\emptyset$
, which leads to a contradiction since wb-irreducible sets are nonempty.
$A=\emptyset$
, which leads to a contradiction since wb-irreducible sets are nonempty.
-
5. Conclusion
(1) This paper delves further into the Jia-Jung problem and the Xi-Zhao model. The latest findings related to the Jia-Jung problem show that every core-compact open well-filtered space is sober, suggesting a connection between core-compactness (and open well-filteredness) and sobriety. Proposition 3.3 in this paper uncovers the link between core-compactness and sobriety, demonstrating that core-compact spaces are precisely those that transform irreducible sets into wb-irreducible sets. Inspired by this result, we introduce the notion of wb-sober spaces and establish their relationship with sober spaces. Specifically, we prove that every open well-filtered space is wb-sober, but not vice versa. Moreover, we show that every core-compact wb-sober space is sober, generalizing Theorem 4.7 of Shen et al. (Reference Shen, Xi, Xu and Zhao2020). On the other hand, we provide sufficient and necessary conditions for the Xi-Zhao model to be core-coherent and routine. Furthermore, using the Xi-Zhao model, we propose a general approach to constructing a non-routine open well-filtered but not well-filtered dcpo.
For a
![]() $T_1$
space
$T_1$
space
![]() $X$
, we show a summary of properties for the Xi-Zhao model
$X$
, we show a summary of properties for the Xi-Zhao model
![]() $\mathbf{D(X)}$
as follows, where a “
$\mathbf{D(X)}$
as follows, where a “
![]() $\checkmark$
” indicates that the properties are preserved, and “
$\checkmark$
” indicates that the properties are preserved, and “
![]() $\times$
” indicates negative cases.
$\times$
” indicates negative cases.
|
|
|
by |
|---|---|---|
| sobriety |
|
Zhao and Xi (Reference Zhao and Xi2018) |
| well-filteredness |
|
Xi and Zhao (Reference Xi and Zhao2017) |
| Choquet completeness |
|
He et al. (Reference He, Xi and Zhao2019) |
| Rudin, weak sobriety |
|
Chen and Li (Reference Chen and Li2022) |
| core-compactness |
|
Chen and Li (Reference Chen and Li2022) |
|
|
(strong) core-coherent | Theorem 4.14 |
| open well-filteredness | Chen and Li (Reference Chen and Li2023) | |
| weak domain | Shen et al. (Reference Shen, Wu and Zhao2019) | |
| locally quasi-algebraic | Zhao and Xi (Reference Zhao and Xi2018) |

(2) Given that Example 4.32 presented is a poset rather than a dcpo, and considering that every first-countable well-filtered space (which is automatically a
![]() $d$
-space) is sober, we pose the following interesting questions for future research:
$d$
-space) is sober, we pose the following interesting questions for future research:
Question 5.1.
-
(1) Is every wb-sober dcpo equipped with the Scott topology open well-filtered?
-
(2) Under what conditions (other than strong core-coherence and core-compactness) is a wb-sober space open well-filtered?
-
(3) Is every first-countable wb-sober (or open well-filtered)
 $d$
-space sober?
$d$
-space sober?
Acknowledgments
This work was supported by the National Natural Science Foundation of China (12101313, 62476030).