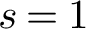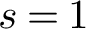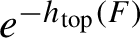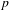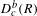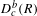Refine search
Actions for selected content:
10 results
8 - A Primer on Zeta Functions and Decomposition Spaces
-
-
- Book:
- Moduli, Motives and Bundles
- Published online:
- 31 October 2025
- Print publication:
- 20 November 2025, pp 233-264
-
- Chapter
- Export citation
ON THE CONVERGENCE OF ZETA FUNCTIONS OF PREHOMOGENEOUS VECTOR SPACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 258 / June 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 311-356
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
VALUES OF ZETA FUNCTIONS OF ARITHMETIC SURFACES AT
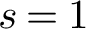 $s=1$
$s=1$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 28 February 2022, pp. 2455-2496
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
There are no deviations for the ergodic averages of Giulietti–Liverani horocycle flows on the two-torus
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 2 / February 2022
- Published online by Cambridge University Press:
- 18 March 2021, pp. 500-513
- Print publication:
- February 2022
-
- Article
- Export citation
MOTIVIC HILBERT ZETA FUNCTIONS OF CURVES ARE RATIONAL
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 31 October 2018, pp. 947-964
- Print publication:
- May 2020
-
- Article
- Export citation
THE p-COHOMOLOGY OF ALGEBRAIC VARIETIES AND SPECIAL VALUES OF ZETA FUNCTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 14 / Issue 4 / October 2015
- Published online by Cambridge University Press:
- 02 June 2014, pp. 801-835
- Print publication:
- October 2015
-
- Article
- Export citation
Analysis on arithmetic schemes. II
-
- Journal:
- Journal of K-Theory / Volume 5 / Issue 3 / June 2010
- Published online by Cambridge University Press:
- 20 May 2010, pp. 437-557
- Print publication:
- June 2010
-
- Article
- Export citation
The convergence of Euler products over p-adic number fields
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 3 / October 2009
- Published online by Cambridge University Press:
- 23 September 2009, pp. 583-606
-
- Article
-
- You have access
- Export citation
Combinatorial L2-determinants
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 43 / Issue 1 / February 2000
- Published online by Cambridge University Press:
- 20 January 2009, pp. 185-194
-
- Article
-
- You have access
- Export citation
Multiple Dirichlet Series and Moments of Zeta and L-Functions
-
- Journal:
- Compositio Mathematica / Volume 139 / Issue 3 / December 2003
- Published online by Cambridge University Press:
- 04 December 2007, pp. 297-360
- Print publication:
- December 2003
-
- Article
-
- You have access
- Export citation