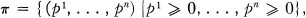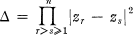Suppose we have a semi-group structure defined on
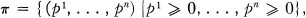
a subset of real Euclidean n-space, En, by (p, q) → F (p, q) = poq. In this note we shall be concerned with a representation T(.) of π as a semi-group of bounded linear operators on a Banach space 𝒳. More particularly, we suppose that postulates P1, P2, P3, P5 and P6 of chapter 25 of (2) are satisfied so that, by Theorem 25.3.1 of that book, there is a continuous function, f(.), defined on π such that f((ρ + σ)a) = f(ρa)o f(σa) for a ∈ π, ρ,σ ≥ 0; that the representation is strongly continuous in a neighbourhood of the origin and that T(0) = I.