Contents
Research Article
Correction to ‘Equivariant spectral decomposition for flows with a ℤ-action’
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 787-791
-
- Article
-
- You have access
- Export citation
An explosion point for the set of endpoints of the Julia set of λ exp (z)
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 177-183
-
- Article
-
- You have access
- Export citation
An algorithm for sofic shift equivalence*
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 381-393
-
- Article
-
- You have access
- Export citation
Differentiability with respect to parameters of average values in probabilistic contracting dynamical systems†
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 599-610
-
- Article
-
- You have access
- Export citation
Book Review
MINIMAL FLOWS AND THEIR EXTENSIONS By J. Auslander: North-Holland1988, 265 pages, ISBN 0444 704531.
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 611-613
-
- Article
-
- You have access
- Export citation
Research Article
×2 and ×3 invariant measures and entropy
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 395-406
-
- Article
-
- You have access
- Export citation
Generic bifurcations of the twist coefficient
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 185-195
-
- Article
-
- You have access
- Export citation
Lorenz attractors through Šil'nikov-type bifurcation. Part I†
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 793-821
-
- Article
-
- You have access
- Export citation
On the topological stable rank of certain transformation group C*-algebras
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 197-207
-
- Article
-
- You have access
- Export citation
Front matter
ETS volume 10 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
The entropy of polynomial diffeomorphisms of C2
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 823-827
-
- Article
-
- You have access
- Export citation
Book Review
The Ergodic Theory Of Discrete Groups By P. J. Nicholls: £19.50, Paperback, 221 pp, ISBN 0 521 37674 2.
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 407-409
-
- Article
-
- You have access
- Export citation
Index to Volume
Index to Volume 10
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 829-830
-
- Article
-
- You have access
- Export citation
Back matter
ETS volume 10 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Front matter
ETS volume 10 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
ETS volume 10 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
ETS volume 10 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation
ETS volume 10 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Index to Volume
Index to Volume 1–10 (1981–1990 inclusive)
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 831-843
-
- Article
-
- You have access
- Export citation
Front matter
ETS volume 10 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
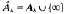 is a connected subspace of the Riemann sphere
is a connected subspace of the Riemann sphere 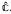 . As a corollary,
. As a corollary,