Let X 1,X 2,X 3,··· be independent, identically distributed random variables with a continuous distribution function and let the sequence of indices {Vr } be defined as follows: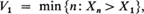 and for r ≧ 1,
and for r ≧ 1,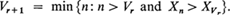 V r is the trial on which the rth (upper) record observation occurs. {V r} will be an infinite sequence of random variables since the underlying distribution function of the X's is continuous. It is well known that the expected value of V r. is infinite for every r (see, for example, Feller [1], page 15). Also define
V r is the trial on which the rth (upper) record observation occurs. {V r} will be an infinite sequence of random variables since the underlying distribution function of the X's is continuous. It is well known that the expected value of V r. is infinite for every r (see, for example, Feller [1], page 15). Also define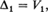 and for r > 1
and for r > 1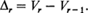 δr is the number of trials between the (r - l)th and the rth record. The distributions of the random variables Vr and δr do not depend on the distribution of the original random variables. It can be shown (see Neuts [2], page 206 or Tata 1[4], page 26) that
δr is the number of trials between the (r - l)th and the rth record. The distributions of the random variables Vr and δr do not depend on the distribution of the original random variables. It can be shown (see Neuts [2], page 206 or Tata 1[4], page 26) that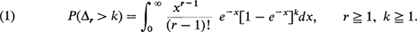 The following theorem is due to Neuts [2].
The following theorem is due to Neuts [2].